粒子群算法
- 1 粒子群算法介绍
- 2 基本思想
- 3 算法流程
- 4 代码实现
1 粒子群算法介绍
粒子群优化算法(PSO:Particle swarm optimization) 是一种进化计算技术(evolutionary computation)。源于对鸟群捕食的行为研究。粒子群优化算法的基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。
PSO的优势在于简单容易实现并且没有许多参数的调节,收敛速度快。目前已被广泛应用于函数优化、神经网络训练、模糊系统控制以及其他遗传算法的应用领域。
相关概念:

适应度函数:来判断当前位置对粒子的吸引力,适应度函数值越大,位置就越好,对粒子的吸引力就越大,那么这个适应度函数值就越有可能是最优解。
2 基本思想
粒子群算法源于对鸟类捕食行为的研究,基本原理是通过种群中个体的信息共享以及协作筛选来寻求最优解。粒子仅具有两个属性:速度和位置,速度是矢量,包括速度大小和方向,位置表示粒子当前所在的坐标。系统首先初始化一组粒子种群,每个粒子都具有一个初始位置和速度,根据评价函数计算得到初始最优解,将其标记成当前个体极值,然后各个粒子之间通过协作共享信息得到群体极值并不断进行迭代,在每一次迭代得到新的个体极值和群体极值后通过下面的公式来更新自己的速度和位置。
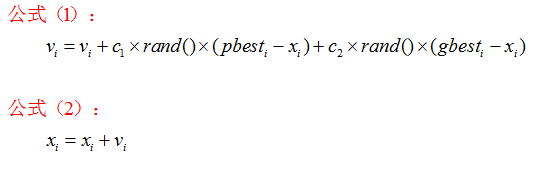
公式(1)的第一部分称为“记忆项”,表示上次速度大小和方向的影响;公式(1)的第二部分称为“个体认知项”,表示粒子在解空间有朝着过去曾经碰到的最优解进行搜索的趋势;公式(1)的第三部分称为“群体认知项”,表示粒子在解空间有朝着整个邻域曾经碰到过的最优解进行搜索的趋势,反映了粒子间的协同合作和知识共享。粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动。
1998年,Shi和Eberhart引入了惯性权重w,并提出动态调整惯性权重以平衡收敛的全局性和收敛速度,该算法被称为标准PSO算法。
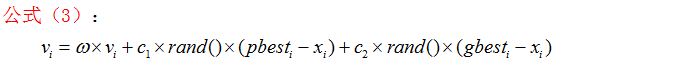
参数详细分析:
- 群体规模N:粒子群中粒子的总数,一般取20~40,对较难或特定类别的问题可以取到100~200。
- 速度,Vi是粒子的速度,最大速度Vmax(大于0),决定当前位置与最好位置之间的区域的分辨率(或精度)。如果Vmax太快,则搜索能力增强,但是粒子容易错过最优解,Vmax较小,开发能力增强,但是粒子容易陷入局部最优。Vmax一般设为每维变量变化范围的10%~20%。如果Vi大于Vmax,则Vi等于Vmax。
- Xi是粒子的当前位置
- rand()是介于(0,1)之间的随机数
- 权重因子:包括惯性因子w和学习因子c1和c2。
-
惯性因子w,其值非负,表示粒子上一代速度对当前代速度的影响,其值较大,全局寻优能力强,局部寻优能力弱,其值较小,全局寻优能力弱,局部寻优能力强。
动态惯性因子能够获得比固定值更好的寻优结果。动态惯性因子可在PSO搜索过程中线性变化,也可以根据PSO性能的某个测度函数动态改变。目前采用较多的是线性递减权值策略。
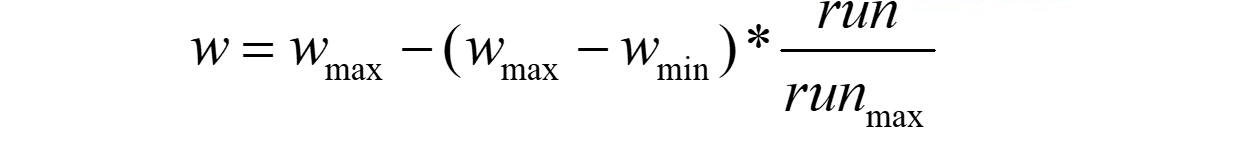
Wmax是最大惯性权重,Wmin是最小惯性权重,run是当前迭代次数,run(max)是算法迭代总次数。当问题空间较大时,随着迭代次数的增加,惯性系数应当不断减少,从而使粒子群算法在初期具有较强的全局搜索能力,以尽可能地获得较大搜索范围,在后期具有较强的局部收敛能力以提高寻优精度。典型权值有0.9和0.4,分别是最大惯性权重和最小惯性权重
-
个体认知因子和群体认知因子c1、c2。如果c1选的太大,就会造成个体认知对粒子的速度产生影响过大,即优先考虑自己认为的最好位置,如果c2选的过大,就会导致社会影响对粒子的速度影响过大,即优先考虑种群的最好位置,如果c1、c2选的过小,就说明,粒子自己当前飞行的速度大小和方向是最稳当的。如果c1 = 0,则只有社会,没有自我,太依赖群体,如果c2 = 0,只有自我认知,没有社会群体,这是最危险的,大家都觉得自己是最优的,都朝着自己认为对的方向飞,那么这个粒子群算法就失去了寻优的能力。如果c1=c2=0,粒子将一直以当前速度的飞行,直到边界。很难找到最优解。通常设c1=c2=2。
当目标函数比较复杂时,普通的粒子群算法容易陷入局部最优,而且后期的收敛速度较慢,这会导致整个算法的效率和精度下降。影响粒子群算法的效率和精度的参数主要有惯性权重w、个体认知因子c1、群体认知因子c2。当w较大时,算法有着更好的全局搜索能力,当w较小时,算法有着更好的局部寻优能力;当c1较小、c2较大时,算法有着更好的局部寻优能力。恰当地选取算法的参数值可以改善算法的性能。
-
3 算法流程
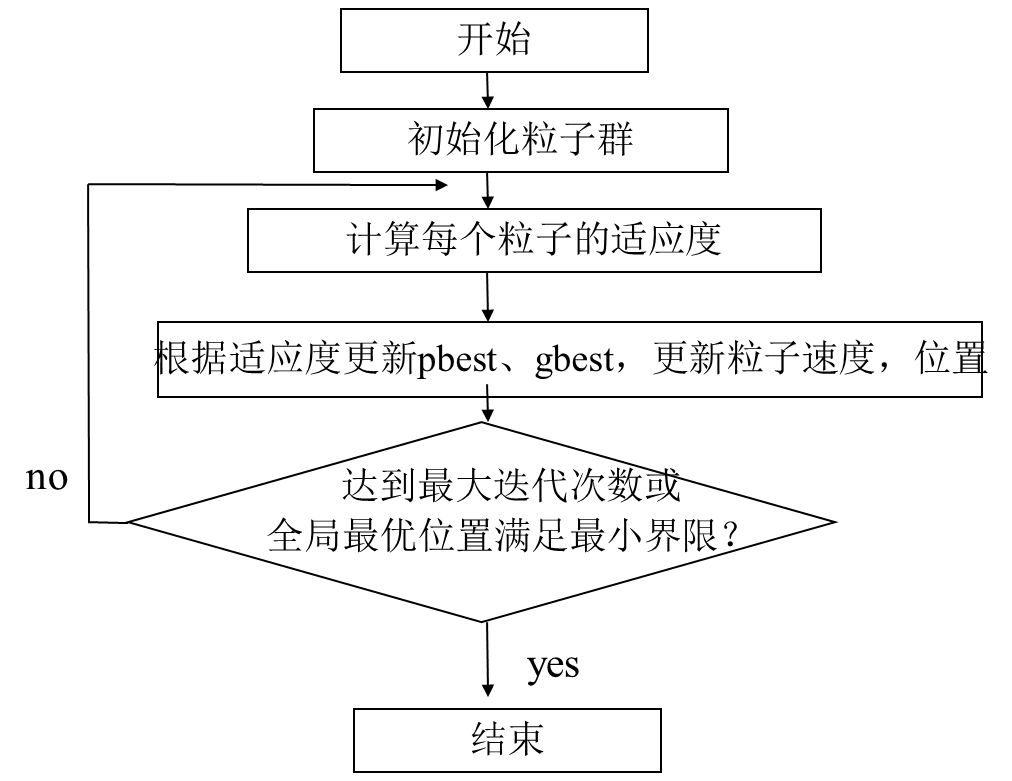
我们尤其要注重把PSO与其它算法,如进化算法、模糊逻辑、生物智能以及混沌等方法或策略相结合,解决PSO易陷入局部最优的问题。
4 代码实现
具体代码如下:
1、定义参数
#define PI 3.14159265358979323846
#define POPSIZE 20 //粒子个数
#define MAXINTERATION 2000 //最大迭代次数
#define NVARS 10 //参数个数
#define WMAX 0.9 //惯量权重最大值
#define WMIN 0.4 //惯量权重最小值
struct particle { //单个粒子
double pBest[NVARS];
double v[NVARS];
double x[NVARS];
double upper[NVARS];
double lower[NVARS];
};
double w; //惯量权重
double c1 = 2.0; //加速因子1
double c2 = 2.0; //加速因子2
double absbound; //上下界绝对值
double vmax; //最大速度
double gBest[NVARS]; //全局最优解
particle particles[POPSIZE]; //粒子群
2、函数定义
double evalfunc(double[], int); //评估函数
double avg(double[], int); //求平均数
double stddev(double[], int); //求标准差
void initialize(int); //初始化函数
double randval(double, double); //求范围(lower,upper)之间的随机数
void evaluate(int); //评估粒子适应值
void update(int, int); //利用更新公式更新每个粒子的速度和位置以及历史最优位置
void fit(void); //更新群体历史最优位置
3、评估函数
double evalfunc(double parameter[], int FUNC = 1) {
/* 10个评估函数 */
/* 通过参数FUNC来选择想要的评估函数 */
if (FUNC == 1) {
double val = 0;
for (int i = 0; i < NVARS; i++) {
val += parameter[i] * parameter[i];
}
return val;
}
if (FUNC == 2) {
double val1 = 0;
double val2 = 0;
for (int i = 0; i < NVARS; i++) {
val1 += abs(parameter[i]);
val2 = val2*abs(parameter[i]);
}
return (val1 + val2);
}
if (FUNC == 3) {
double val1 = 0;
int i, j;
for (i = 0; i < NVARS; i++) {
double val2 = 0;
for (j = 0; j < i; j++) {
val2 += parameter[j];
}
val1 += val2*val2;
}
return val1;
}
if (FUNC == 4) {
double val = 0;
for (int i = 0; i < NVARS; i++) {
if (abs(parameter[i]) > val)
val = abs(parameter[i]);
}
}
if (FUNC == 5) {
double val = 0;
for (int i = 0; i < NVARS - 1; i++) {
val += 100 * (parameter[i + 1] - parameter[i] * parameter[i])*(parameter[i + 1] - parameter[i] * parameter[i]) + (parameter[i] - 1)*(parameter[i] - 1);
}
return val;
}
if (FUNC == 6) {
double val = 0;
for (int i = 0; i < NVARS; i++) {
val += floor(parameter[i] + 0.5)*floor(parameter[i] + 0.5);
}
return val;
}
if (FUNC == 7) {
double val = 0;
for (int i = 0; i < NVARS; i++) {
val += i*pow(parameter[i], double(i));
}
return (val + randval(0, 1));
}
if (FUNC == 8) {
double val = 0;
for (int i = 0; i < NVARS; i++) {
val += (-(parameter[i] * sin(sqrt(abs(parameter[i])) / 180 * PI)));
}
return val;
}
if (FUNC == 9) {
double val = 0;
for (int i = 0; i < NVARS; i++) {
val += (parameter[i] * parameter[i] - 10 * cos(2 * PI*parameter[i] / 180 * PI) + 10.0);
}
return val;
}
if (FUNC == 10) {
double val1 = 0;
double val2 = 0;
for (int i = 0; i < NVARS; i++) {
val1 += parameter[i] * parameter[i];
val2 += cos(2 * PI*parameter[i] / 180 * PI);
}
return ((-20)*exp((-0.2)*sqrt(val1 / NVARS)) - exp(val2 / NVARS) + 20 + exp(1));
}
}
4、一些计算指标及随机数函数
double avg(double parameter[], int n) {
double num = 0;
for (int i = 0; i < n; i++) {
num += parameter[i];
}
return num / n;
}
double stddev(double parameter[], int n) {
double num = avg(parameter, n);
double sum = 0.0;
for (int i = 0; i < n; i++) {
sum += (parameter[i] - num)*(parameter[i] - num);
}
return sqrt(sum / n);
}
double randval(double low, double high) {
return (low + (high - low)*rand()*1.0 / RAND_MAX);
}
5、初始化函数
void initialize(int FUNC = 1) {
/* 初始化每个粒子的速度、位置并将 */
/* 该位置设定为当前历史最优位置找 */
/* 到所有粒子的最优位置并设定为当 */
/* 前群体历史最优位置 */
int i, j;
double lbound[NVARS];
double ubound[NVARS];
for (i = 0; i < NVARS; i++) {
lbound[i] = (-absbound);
ubound[i] = absbound;
}
for (i = 0; i < NVARS; i++) {
for (j = 0; j < POPSIZE; j++) {
particles[j].upper[i] = ubound[i];
particles[j].lower[i] = lbound[i];
particles[j].v[i] = randval(lbound[i], ubound[i]);
particles[j].x[i] = randval(lbound[i], ubound[i]);
particles[j].pBest[i] = particles[j].x[i];
}
}
double pval = evalfunc(particles[0].pBest);
int num;
for (i = 1; i < POPSIZE; i++) {
if (pval > evalfunc(particles[i].pBest)) {
pval = evalfunc(particles[i].pBest);
num = i;
}
else continue;
}
for (j = 0; j < NVARS; j++) {
gBest[j] = particles[num].pBest[j];
}
}
6、评估
void evaluate(int FUNC = 1) {
/* 通过传入参数FUNC来调用不同的评 */
/* 估函数并对粒子位置进行评估并更 */
/* 新粒子历史最优位置 */
int i, j;
double pval[POPSIZE], nval[POPSIZE];
for (i = 0; i < POPSIZE; i++) {
pval[i] = evalfunc(particles[i].pBest, FUNC);
nval[i] = evalfunc(particles[i].x, FUNC);
if (pval[i] > nval[i]) {
for (j = 0; j < NVARS; j++) {
particles[i].pBest[j] = particles[i].x[j];
}
}
}
}
7、更新函数
void update(int interation, int w_change_method = 1) {
/* 通过参数w_change_method来选择不 */
/* 同的惯性权重衡量规则来根据群体 */
/* 历史最优位置更新粒子速度以及位置*/
int i, j;
double v, x;
if (w_change_method == 1) {
w = WMAX - (WMAX - WMIN) / MAXINTERATION*(double)interation;
}
else if (w_change_method == 2) {
w = randval(0.4, 0.6);
}
else if (w_change_method == 3) {
w = WMAX - (WMAX - WMIN)*((double)interation / MAXINTERATION)*((double)interation / MAXINTERATION);
}
else if (w_change_method == 4) {
w = WMIN + (WMAX - WMIN)*((double)interation / MAXINTERATION - 1)*((double)interation / MAXINTERATION - 1);
}
else {
cout << "Dont have this weight change method!";
return;
}
for (i = 0; i < NVARS; i++) {
for (j = 0; j < POPSIZE; j++) {
v = w*particles[j].v[i] + c1*randval(0, 1)*(particles[j].pBest[i] - particles[j].x[i]) + c2*randval(0, 1)*(gBest[i] - particles[j].x[i]);
if (v > vmax)particles[j].v[i] = vmax;
else if (v < (-vmax))particles[j].v[i] = (-vmax);
else particles[j].v[i] = v;
x = particles[j].x[i] + particles[j].v[i];
if (x > particles[j].upper[i])particles[j].x[i] = particles[j].upper[i];
else if (x < particles[j].lower[i])particles[j].x[i] = particles[j].lower[i];
else particles[j].x[i] = x;
}
}
}
8、适应函数
void fit(void) {
/* 更新群体最优位置 */
int i, j;
double gval = evalfunc(gBest);
double pval[POPSIZE];
for (i = 0; i < POPSIZE; i++) {
pval[i] = evalfunc(particles[i].pBest);
if (gval > pval[i]) {
for (j = 0; j < NVARS; j++) {
gBest[j] = particles[i].pBest[j];
}
}
}
}
9、main函数
int main() {
srand(time(NULL));
double all_gBest[100];
int i, j, k;
int FUNC;
int w_change_method;
cout << "*********************************************************************************************************************************" << endl;
cout << "******************************* 十个" << NVARS << "维函数用4种不同的权重控制方法运行一百次的平均结果及标准差" << " *******************************" << endl;
cout << " 线性递减法" << " 随机权重法" << " 凹函数递减法" << " 凸函数递减法" << endl;
cout << " 函数" << endl;
cout << " 平均值" << " 标准差"
<< " 平均值" << " 标准差"
<< " 平均值" << " 标准差"
<< " 平均值" << " 标准差";
cout << endl << endl;
for (FUNC = 1; FUNC <= 10; FUNC++) {
cout << " " << std::left << "f" << setw(4) << FUNC;
switch (FUNC)
{
case 1:absbound = 100.0; break;
case 2:absbound = 10.0; break;
case 3:absbound = 100.0; break;
case 4:absbound = 100.0; break;
case 5:absbound = 30.0; break;
case 6:absbound = 100.0; break;
case 7:absbound = 1.28; break;
case 8:absbound = 500.0; break;
case 9:absbound = 5.12; break;
case 10:absbound = 32.0; break;
default:
break;
}
vmax = absbound*0.15;
for (w_change_method = 1; w_change_method <= 4; w_change_method++) {
for (j = 0; j < 100; j++) {
initialize();
evaluate(FUNC);
for (int i = 0; i < MAXINTERATION; i++) {
update(i, w_change_method);
evaluate(FUNC);
fit();
}
double evalue = evalfunc(gBest);
if (evalue == 0) {
j--;
continue;
}
all_gBest[j] = evalue;
}
cout << setw(16) << avg(all_gBest, 100);
cout << setw(16) << stddev(all_gBest, 100);
}
cout << endl;
}
cout << "********************************************************* 算法运行结束 ********************************************************" << endl;
cout << "*********************************************************************************************************************************" << endl;
system("pause");
}
参考资料:https://blog.csdn.net/darin1997/article/details/80675933?spm=1001.2014.3001.5506