目录
1.介绍和实现
2.仿函数和函数对象
3.oj
4.反向迭代器
1.介绍和实现
他也在<queue>的头文件里
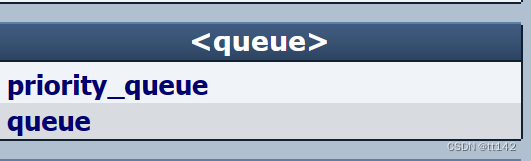
但是他的底层是堆,并不满足先入先出(不要一看到queue就先入先出)

他也是一个容器适配器,用vector适配的,为什么?因为他底层是一个堆,之前就说过堆这种结构就是一个顺序表
那么这个实现岂不是爽歪歪, 堆的复习在这里
直接写了,没什么新东西
namespace wrt
{
template<class T,class Container=vector<T>>
class priority_queue
{
public:
priority_queue()
{}
template <class InputIterator>
priority_queue(InputIterator first, InputIterator last)
:_con(first,last)
{
for (size_t i= (_con.size() - 1 - 1 )/ 2; i >=0; i--)//一个节点-1 /2 是用来算父亲节点的
{
//向下调整
adjust_down(i);
}
}
void adjust_up(size_t child) //违背祖宗...
{
size_t parent = (child - 1) / 2;
while (child >0)
{
if (_con[child] > _con[parent])
{
swap(_con[child], _con[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void adjust_down(size_t parent)
{
size_t child = 2 * parent + 1;//假设是左孩子,并且左孩子是最大的孩子
while (child < _con.size())
{
if (child + 1 < _con.size()&&_con[child + 1] > _con[child] )
{
child ++;
}
//此时的child已经是最大的孩子
if (_con[parent] < _con[child])
{
swap(_con[parent], _con[child]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
void push(const T& x)//插入数据就是向上调整
{
_con.push_back(x);
adjust_up(_con.size() - 1);
}
void pop()
{
swap(_con[0], _con[_con.size() - 1]);
_con.pop_back();
adjust_down(0);
}
const T& top() const
{
return _con[0];
}
bool empty() const
{
return _con.empty();
}
size_t size()
{
return _con.size();
}
private:
Container _con;
};
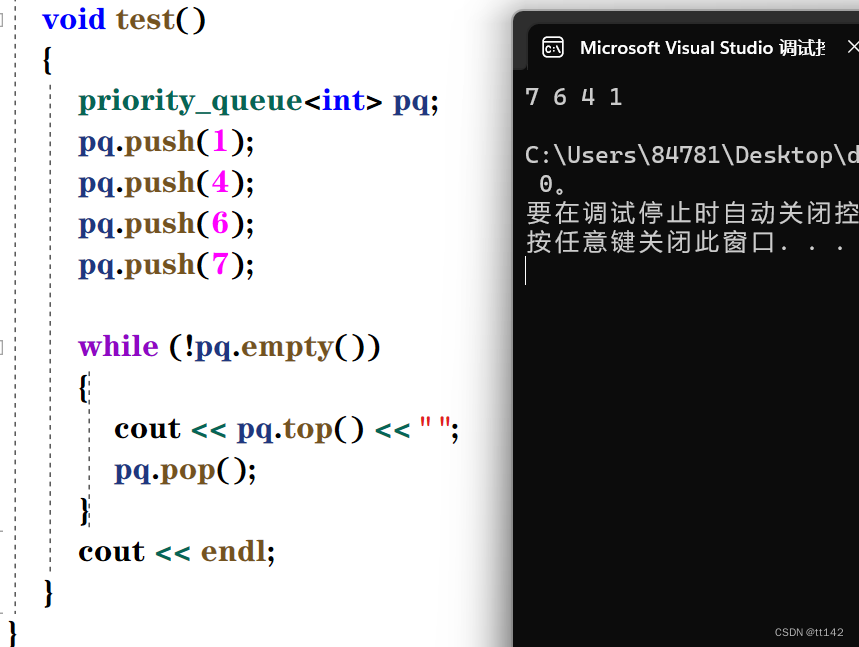
void test()
{
priority_queue<int> pq;
pq.push(1);
pq.push(4);
pq.push(6);
pq.push(7);
while (!pq.empty())
{
cout << pq.top() << " ";
pq.pop();
}
cout << endl;
}
}2.仿函数和函数对象

注意到这有一个类,其实仿函数也是一个类,仿函数类型的 对象 叫函数对象(因为他可以像函数一样使用)
namespace wrt
{
template<class T>
struct less
{
bool operator()(const T& x, const T& y)
{
return x < y;
}
};
template<class T>
struct greater
{
bool operator()(const T& x, const T& y)
{
return x > y;
}
};
}这里的less类和greater类就是两个仿函数,
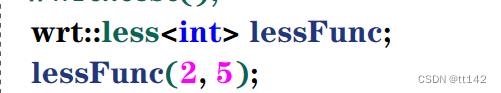
lessFunc是仿函数less实例化对象,根据前面的定义,他叫函数对象
实例化之后我们看lessFunc()这个形式就很像函数调用有木有,所以这就是函数对象的特征:像函数一样使用
那么仿函数存在的意义是什么?
回顾之前C里学过的比较函数,qsort最经典的 最后一个参数需要比较函数
还有快排,冒泡....我们自己写过的函数
void BubbleSort(T* a, int n)
{
for (int j = 0; j < n; ++j)
{
int exchange = 0;
for (int i = 1; i < n - j; ++i)
{
if (a[i] < a[i - 1])
{
swap(a[i - 1], a[i]);
exchange = 1;
}
}
if (exchange == 0)
{
break;
}
}
}这样写就把函数写死了
但用一下仿函数
void BubbleSort(T* a, int n, Compare com)
{
for (int j = 0; j < n; ++j)
{
int exchange = 0;
for (int i = 1; i < n - j; ++i)
{
//if (a[i] < a[i - 1])
if (com(a[i], a[i - 1]))
{
swap(a[i - 1], a[i]);
exchange = 1;
}
}
if (exchange == 0)
{
break;
}
}
}写成这样我们根本不知道这个函数是升序降序
但是根据我的要求,他是可控的


所以这就是升序
想要降序?
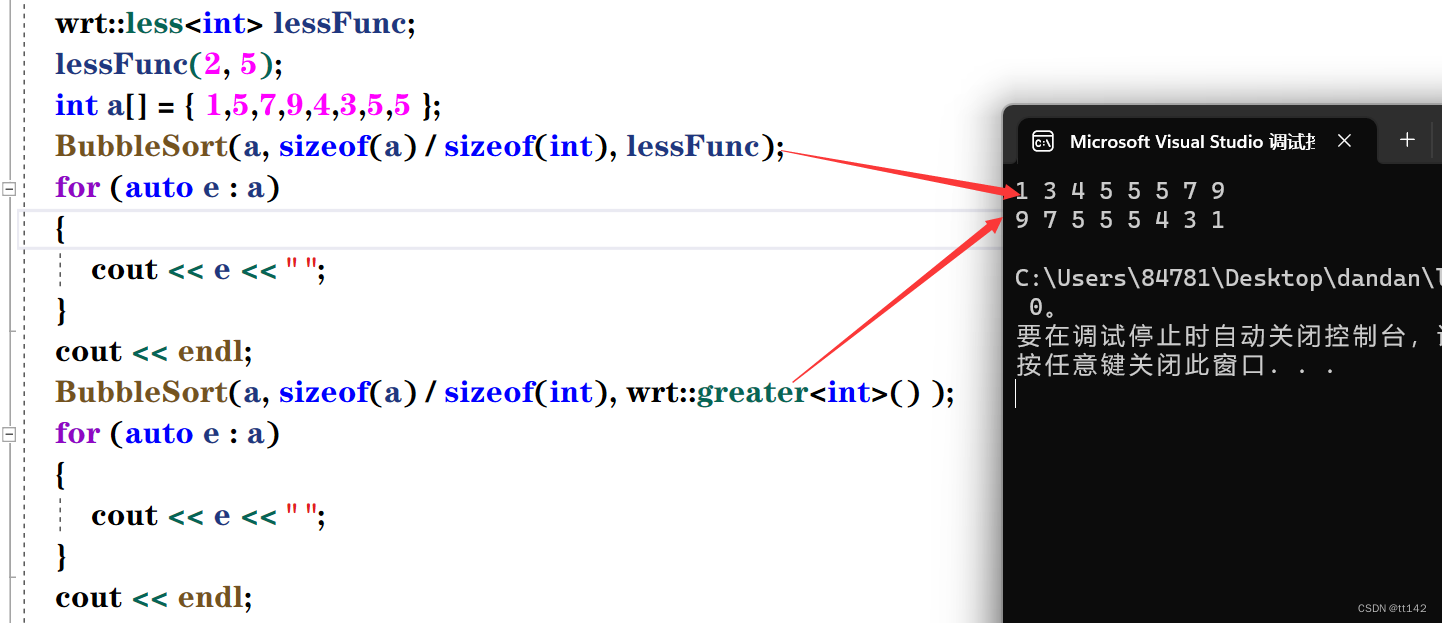
这个降序就是匿名函数实现的,如果我只有这一块需要用到greater仿函数类,那就匿名函数更省事,反之还是像less仿函数那么写就好了
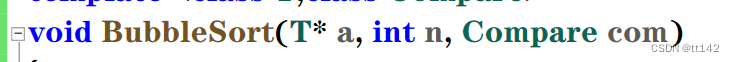
这个地方com类型需要是const & 吗?其实没太大必要,要不然你上面的仿函数类的运算符()重载还得写成const的,因为这个com根本不大,仿函数里面没有成员变量,所以不就是1字节
我们平时加上const& 就是为了防止参数过大,可以不需要拷贝构造一次
那么我们把仿函数应用在刚才写的堆里面
向上调整的比较部分可以更改,一定要注意,库里面默认就是大堆用less
less是x < y ,所以要注意顺序com(_con[parent],_con[child]) ——com(x,y)
void adjust_up(size_t child) //违背祖宗...
{
Compare com;
size_t parent = (child - 1) / 2;
while (child >0)
{
if(com(_con[parent],_con[child]))
//if (_con[child] > _con[parent])
{
swap(_con[child], _con[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}然后向下调整部分的比较也改一下
void adjust_down(size_t parent)
{
Compare com;
size_t child = 2 * parent + 1;//假设是左孩子,并且左孩子是最大的孩子
while (child < _con.size())
{
// if (child + 1 < _con.size() && _con[child + 1] > _con[child])
if (child + 1 < _con.size() && com( _con[child],_con[child + 1])
{
child++;
}
//此时的child已经是最大的孩子
//if (_con[parent] < _con[child])
if (com(_con[parent], _con[child]))
{
swap(_con[parent], _con[child]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}运行一下发现刚刚好
现在想实现小堆怎么搞?

实例化的时候不再使用缺省参数,缺省了就是堆的默认(大堆)
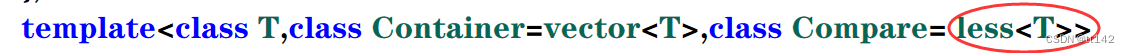
变成这样

现在玩点花的,看一下之前写过的日期类,我们用仿函数比较日期
日期类![]()
class Date
{
public:
Date(int year = 1900, int month = 1, int day = 1)
: _year(year)
, _month(month)
, _day(day)
{}
bool operator<(const Date& d)const
{
return (_year < d._year) ||
(_year == d._year && _month < d._month) ||
(_year == d._year && _month == d._month && _day < d._day);
}
bool operator>(const Date& d)const
{
return (_year > d._year) ||
(_year == d._year && _month > d._month) ||
(_year == d._year && _month == d._month && _day > d._day);
}
friend ostream& operator<<(ostream& _cout, const Date& d)
{
_cout << d._year << "-" << d._month << "-" << d._day;
return _cout;
}
private:
int _year;
int _month;
int _day;
}; 发现很对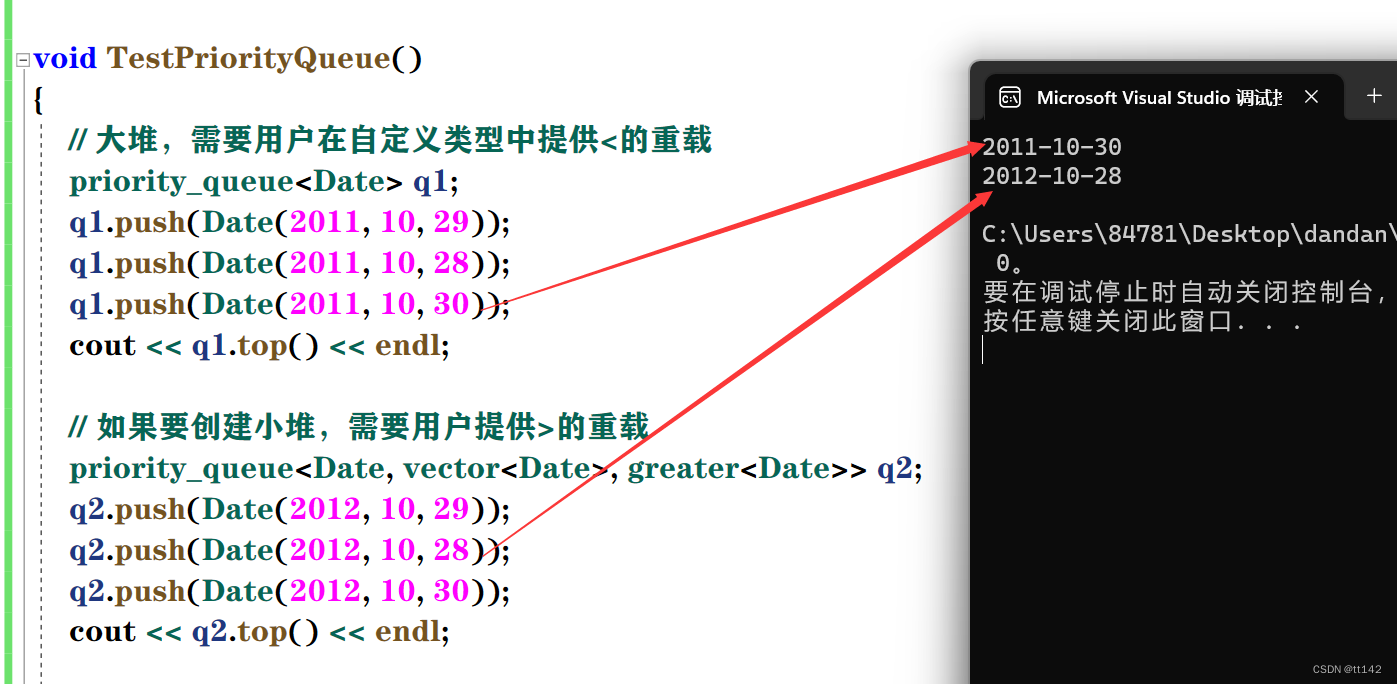
但是如果T是日期类指针
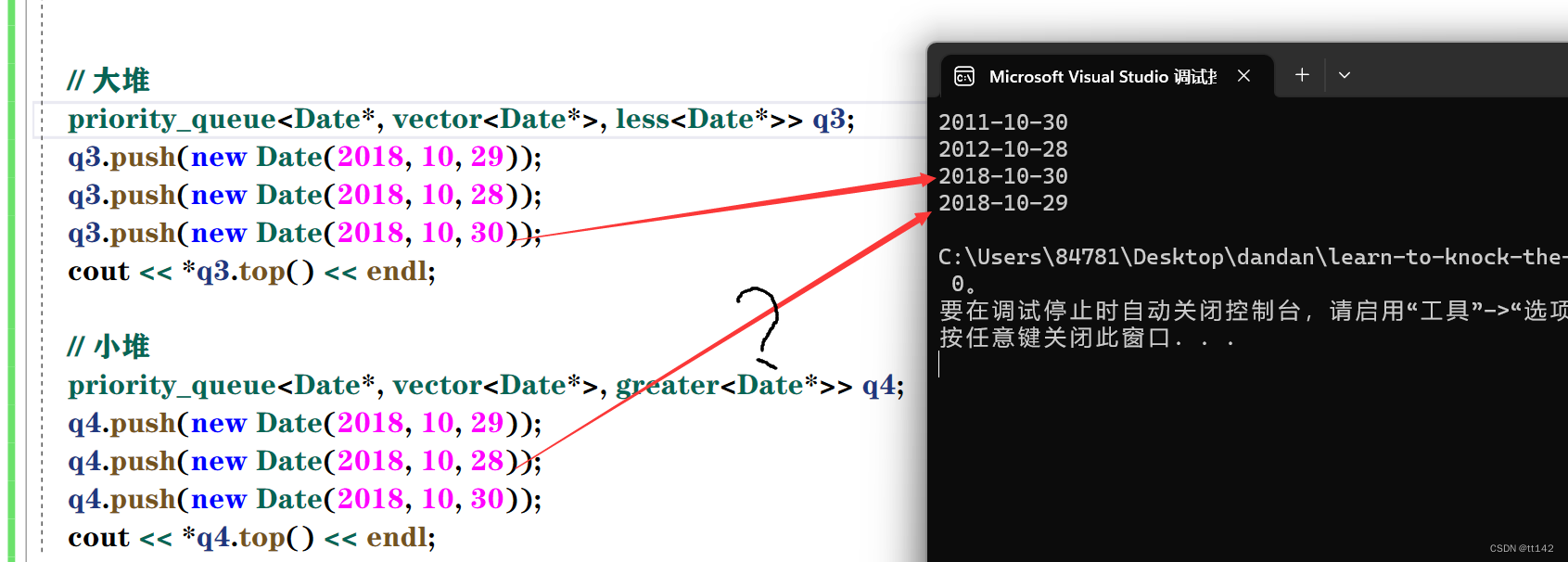
怎么不对?小堆的堆顶不是最小的日期,这个函数首先肯定没写错,并且发现每次运行的结果居然都不一样,这时候仿函数比较的就是地址,每次new的地址都是随机的,所以不一定哪个日期的地址就大/小
这个不符合我们预期,怎么办?
自己写仿函数,因为刚才的less就是自己写的,所以再造一个很轻松
struct PDateLess
{
bool operator()(const Date* d1, const Date* d2)
{
return *d1 < *d2;
}
};
struct PDateGreater
{
bool operator()(const Date* d1, const Date* d2)
{
return *d1 > *d2;
}
}; 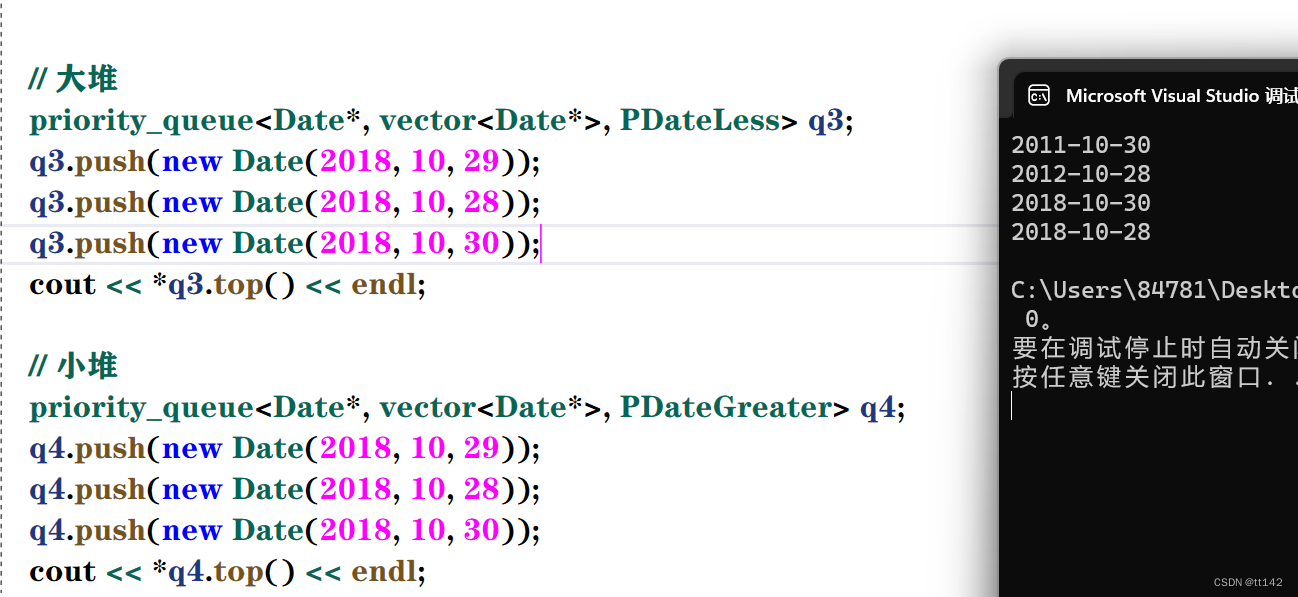
这样就没问题啦,所以这也是泛型,之前的泛型都是数据类型的广泛支持,但是现在他一定程度上也影响了我们的逻辑
但是现在的仿函数只是冰山一角,现在浅看一下,更复杂的我们以后慢慢学习
3.oj
数组中第K大的数字
可以建小堆,或者大堆
建大堆,然后pop k-1次就可以取到第k大,这个是时间复杂度就是O(N+(k-1)*logN)
N个元素建堆是O(N),然后popk-1次就是 (k-1)*logN
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
priority_queue<int>pq(nums.begin(),nums.end()) ;
while(--k)
{
pq.pop();
}
return pq.top();
}
};还可以建k个数字的小堆,堆顶就是k个数中最小的,每次有更大的就进堆,然后向下调整
最后堆顶就是第k最大,时间复杂度O(k+(n-k)*logn)
k个数字建小堆,然后剩下的最坏情况每一次比较之后都可以入,就是(n-k)*logn
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
priority_queue<int,vector<int>,greater<int>> pq(nums.begin(),nums.begin()+k) ;
for(size_t i=k;i<nums.size();i++)
{
if(nums[i]>pq.top())
{
pq.pop();
pq.push(nums[i]);
}
}
return pq.top();
}
};4.反向迭代器
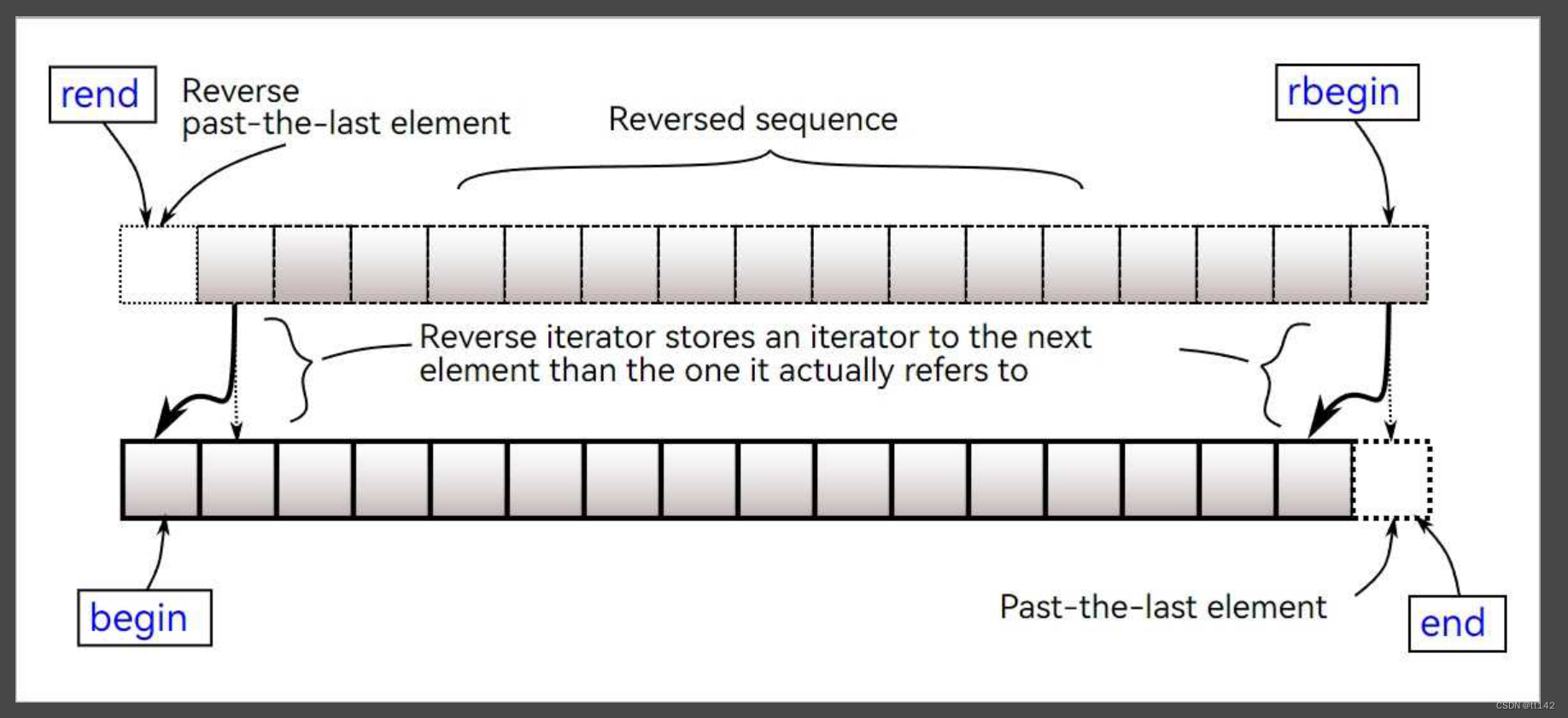
泛型思维去理解,这个反向迭代器肯定是用正向迭代器封装的
template<class Iterator>
class ReverseIterator
{
typedef ReverseIterator<Iterator> Self;
public:
ReverseIterator(Iterator it)
:_it(it)
{}
Self& operator++()
{
--_it;
return *this;
}
Self& operator--()
{
++_it;
return *this;
}
bool operator!= (const Self& s) const
{
return _it != s._it;
}
private:
Iterator _it;
};
上面的函数都很简单嘛,但是*运算符重载怎么写?
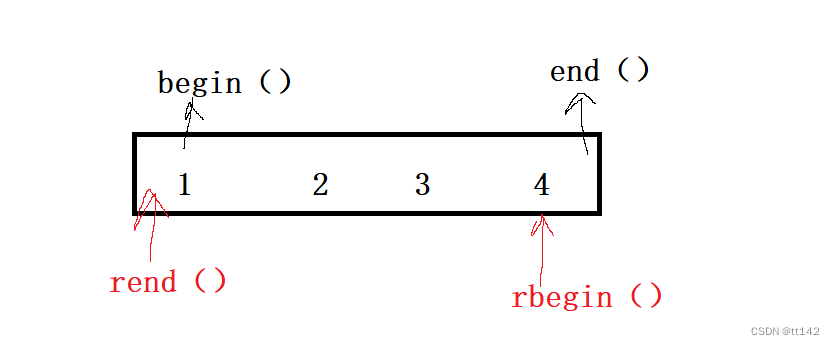
下面是反向迭代器的错误理解
正确理解大佬的思路(对称美)
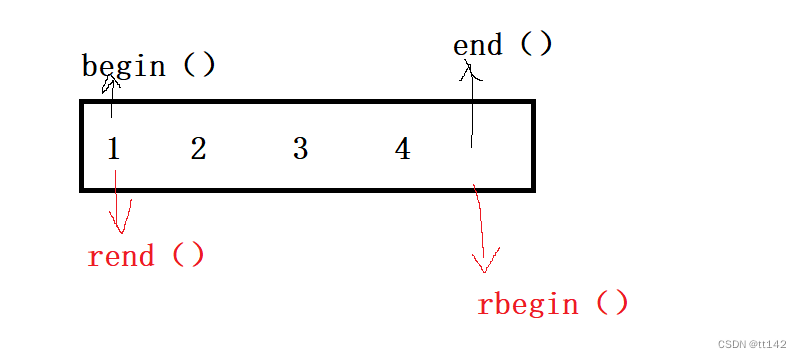
正常解引用就很坑 ,需要返回前一个位置,但是我不知道数据类型,库里面的方式就是萃取,绕了很多层,但是我们还可以用之前 那个多传几个模板的思路
template<class Iterator, class Ref, class Ptr>
class ReverseIterator
{
typedef ReverseIterator<Iterator, Ref, Ptr> Self;
public:
ReverseIterator(Iterator it)
:_it(it)
{}
Ref operator*()
{
Iterator tmp = _it;
return *(--tmp);
}
Ptr operator->()
{
return &(operator*());
}
Self& operator++()
{
--_it;
return *this;
}
Self& operator--()
{
++_it;
return *this;
}
bool operator!= (const Self& s) const
{
return _it != s._it;
}
private:
Iterator _it;
};
然后list.cpp的源文件里这个反向迭代器.h一包含

这样就可以使用啦,当然在vector里面也可以同样方法使用