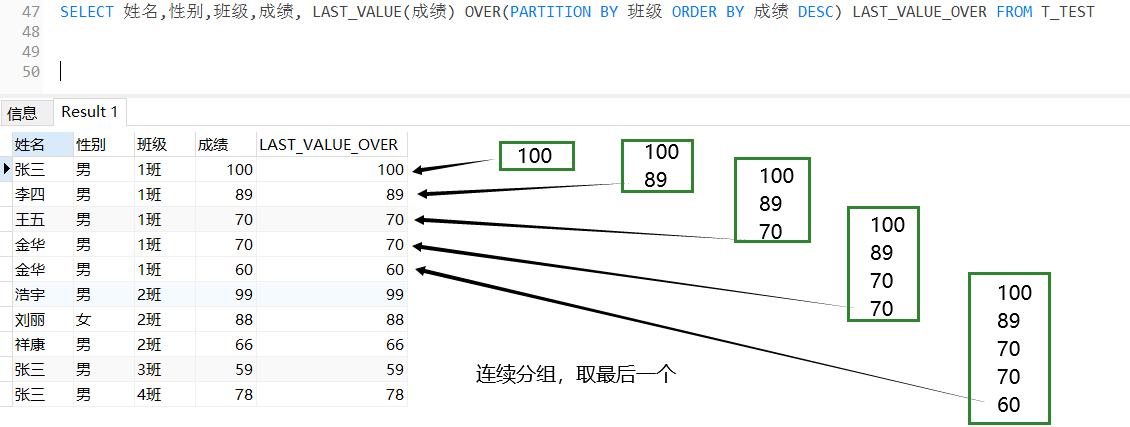
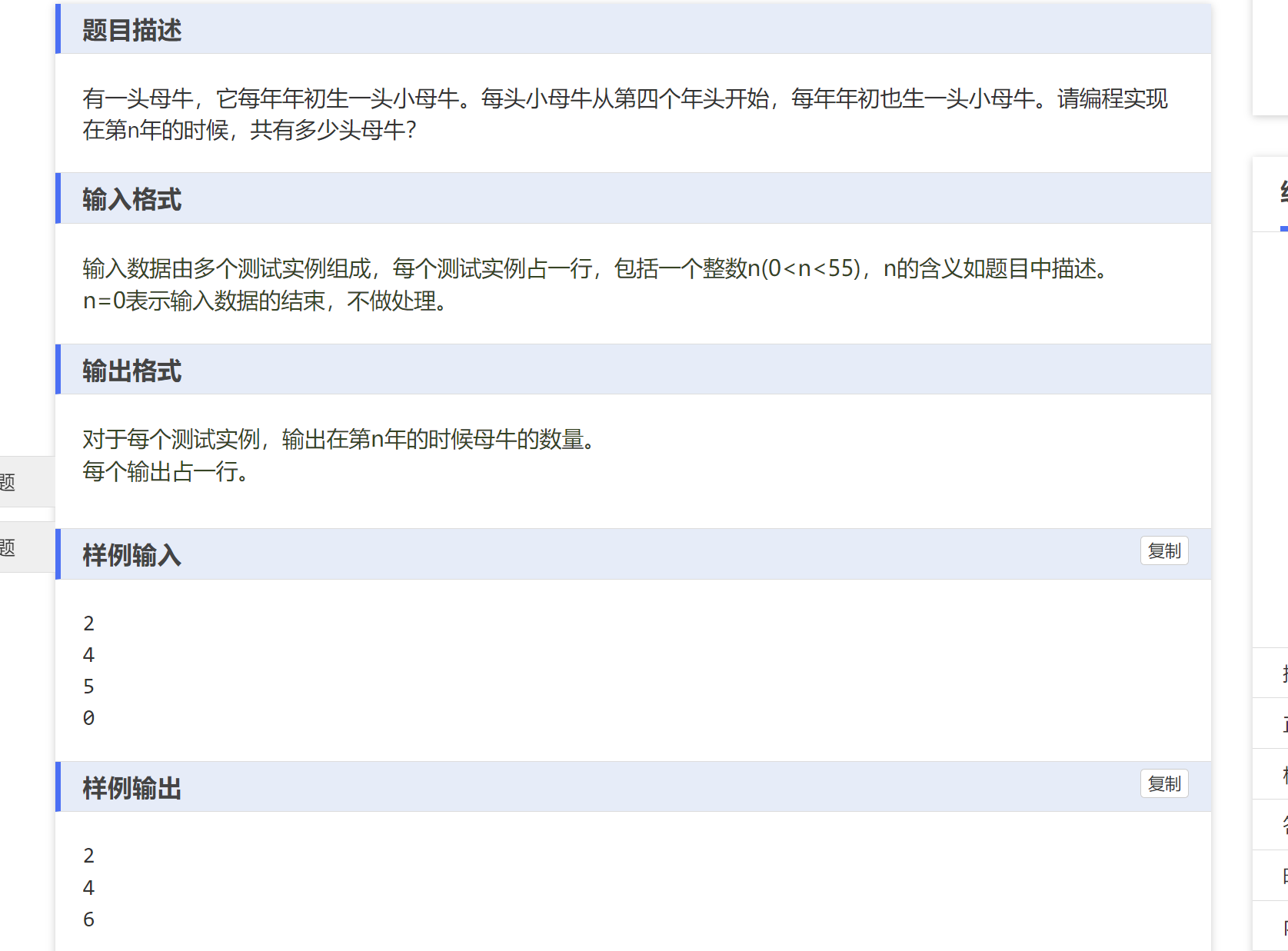
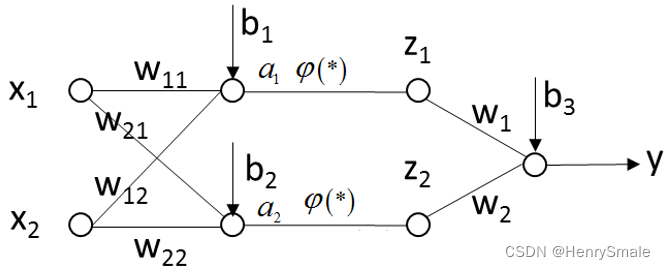
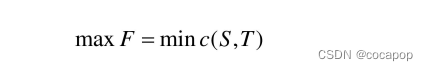题目大意

给你一个数$k$，请你构造一棵节点数量小于等于5000的直径数量为$k$的树。

我们定义这棵树的直径为，所有满足$1\le i<j\le n$的$(i,j)$中，$dis(i,j)$最大的。如果有多个这样的$(i,j)$，那么均为直径。

$1\le k\le 5\times 10^6,0\le w_i\le 10^5$，$w_i$表示第$i$条边的边权。

题解

构造一个菊花图，根节点有三个儿子，每个儿子所在的子树大小分别为$a,b,c$且都是一条由权值为0的边组成的链，那么直径为$ab+bc+ca$。

我们需要令$k=ab+ac+bc=(a+c)(b+c)-c^2$。

我们可以枚举$c$，将$k+c^2$分解质因数，直到找到合适的$(a,b,c)$即可。

经过计算可以证明有很高的概率存在这样合适的解，实际上对于所有的$k$都如此。

时间复杂度为$O(n\sqrt{k})$。

当然，这种方法不一定完全正确，有可能需要四个或更多儿子才能构造出。更好的方法，请看我的另一篇博客。

code

#include<bits/stdc++.h>
using namespace std;
int n,tot=0,vt=1,fl=0;
struct node{
	int x,y,z;
}w[10005];
void dd(int v){
	for(int i=1;i<=v-1;i++){
		w[++tot]=(node){vt,vt+1};++vt;
	}
}
int main()
{
	scanf("%d",&n);
	for(int a,b,c=1;c<=5000;c++){
		int v=n+c*c;
		for(int i=c;i*i<=v;i++){
			if(v%i>0) continue;
			a=i-c;b=v/i-c;
			if(a>=0&&b>=0&&a+b+c+1<=5000){
				if(a){
					w[++tot]=(node){1,++vt,1};
					dd(a);
				}
				if(b){
					w[++tot]=(node){1,++vt,1};
					dd(b);
				}
				if(c){
					w[++tot]=(node){1,++vt,1};
					dd(c);
				}
				fl=1;break;
			}
		}
		if(fl) break;
	}
	printf("%d\n",vt);
	for(int i=1;i<=tot;i++){
		printf("%d %d %d\n",w[i].x,w[i].y,w[i].z);
	}
	return 0;
}

一些思考

如果$w_i$不能为$0$，怎么办呢？我们把根节点的每个儿子分别设置对应多个儿子，使得这些儿子没有儿子且到其父亲边权为1即可。