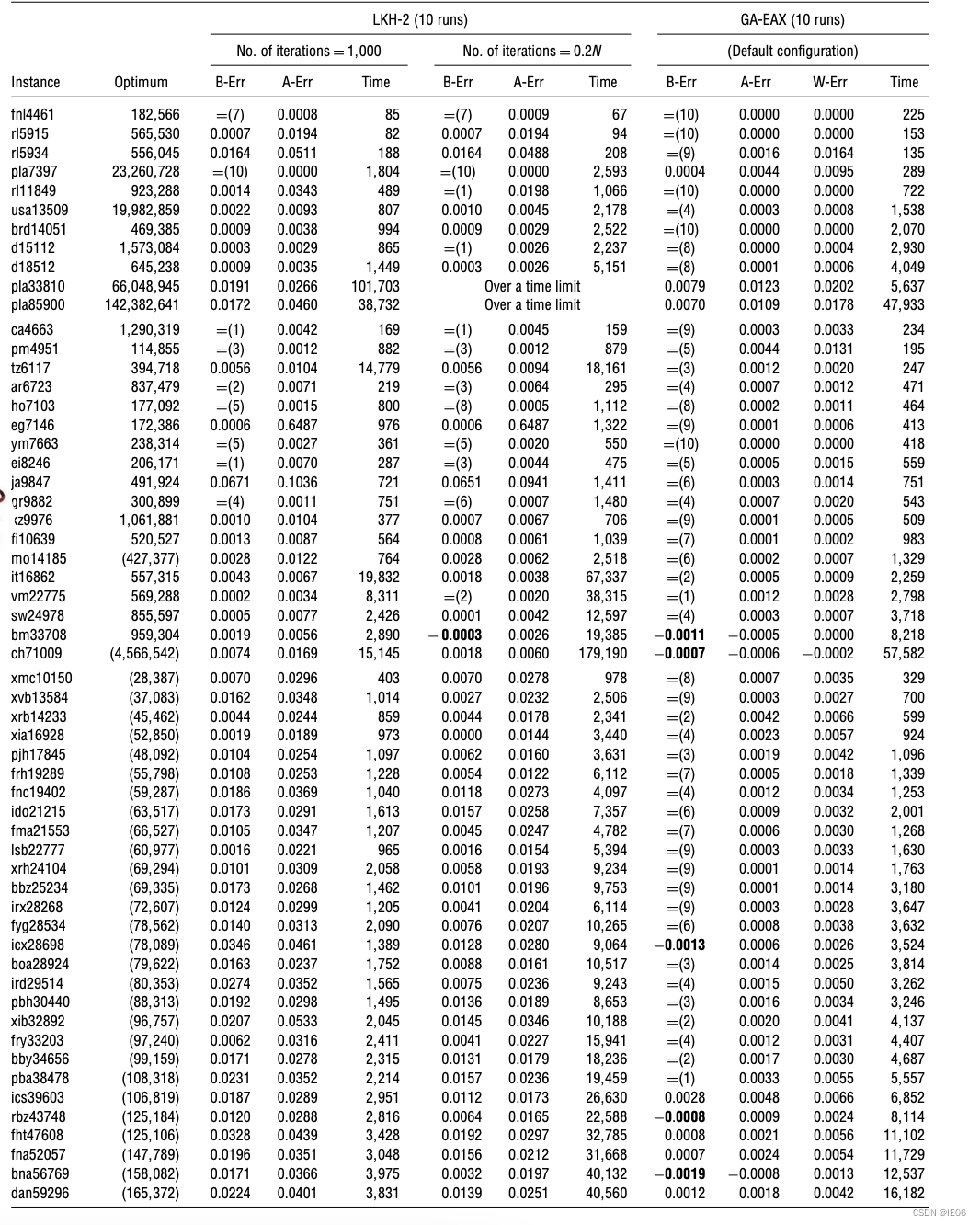
背景:
在vtk使用过程中,我们有时要搜索点或者cell最近的 单元, 仔细看源码,有时无法判断其具体是什么样子,因而这里做了可视化处理,方便我们更深刻的理解 vtkPointLocator 类型函数的使用;
过程:
1.了解其继承关系是必要的:
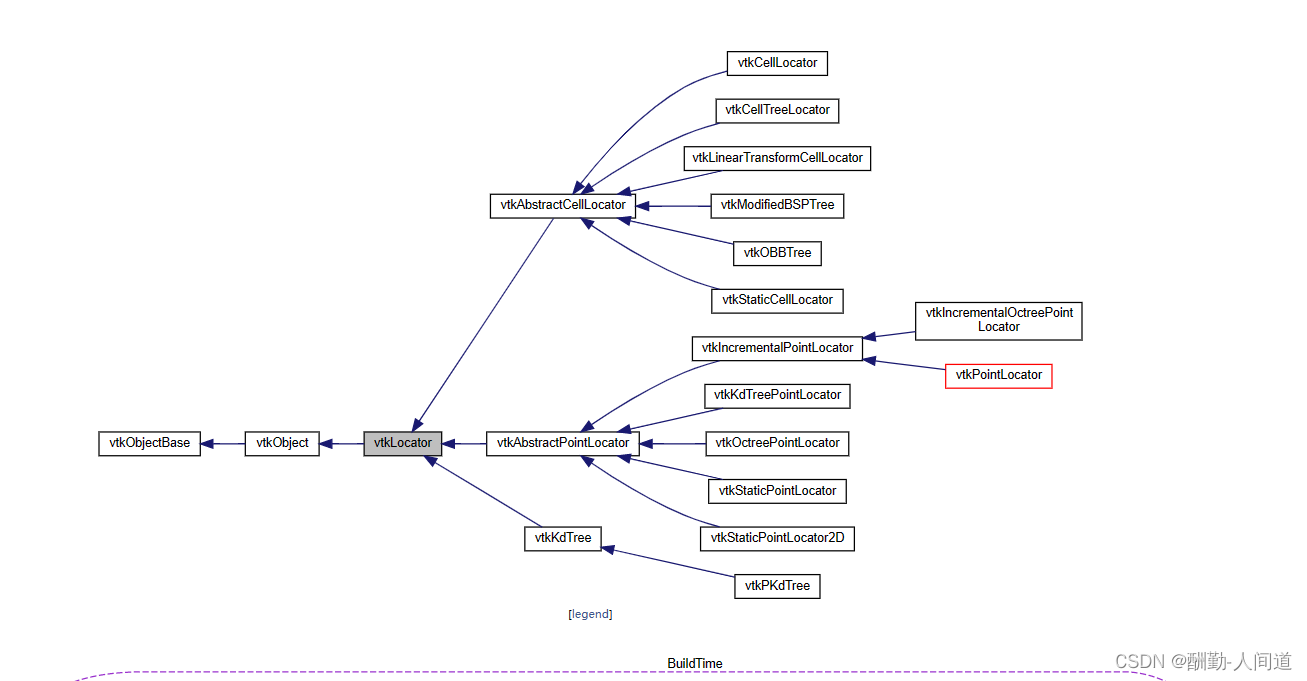
2.开始探索该函数的一些效果:
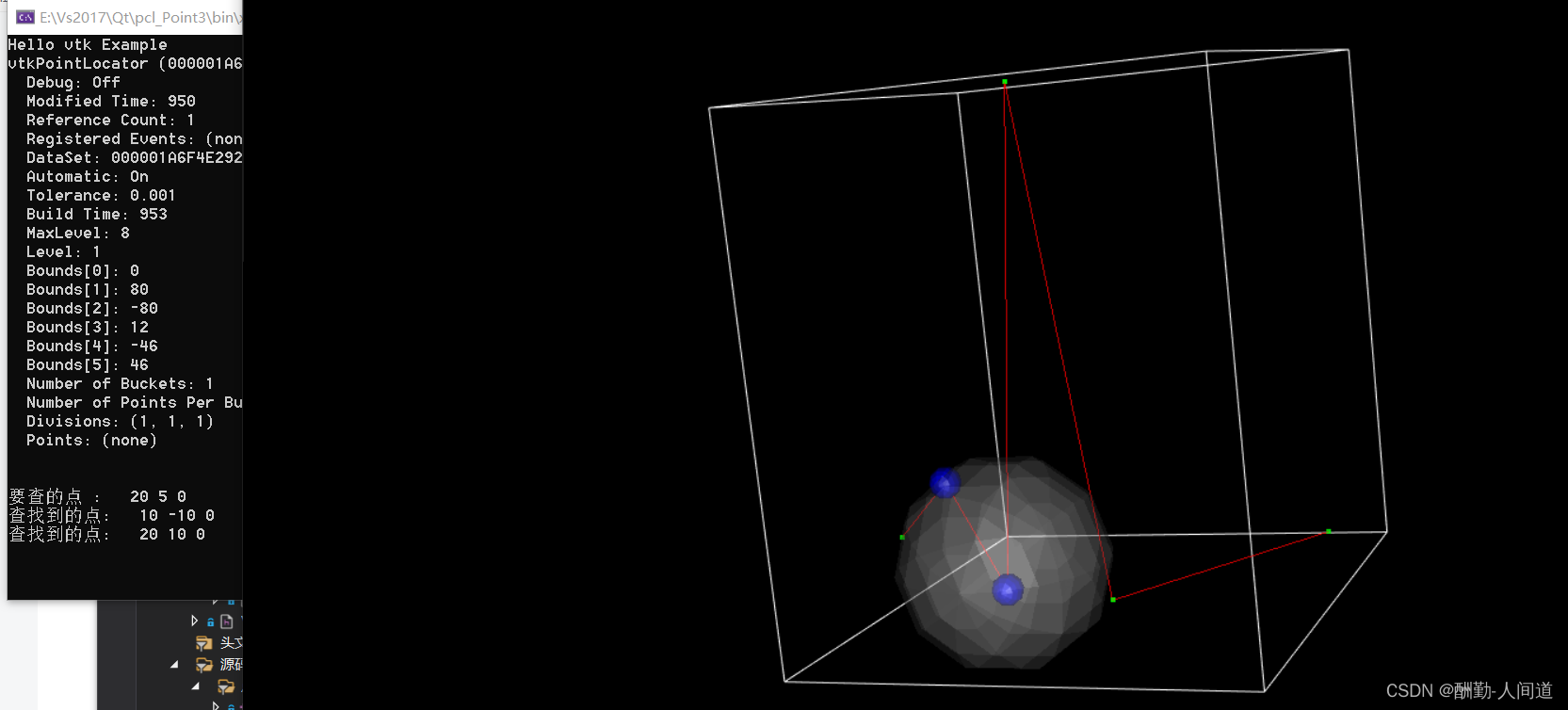
我们会将原始数据以 绿色 小球表示, 范围 R 用白色透明标识 , 搜索到的点,用 蓝色标识
2.1. 准备数据集.
std::vector<std::array<double, 3>> mPointSource;
//vtkNew<vtkMinimalStandardRandomSequence> rm;
准备一份数据..... 包含 几何数据,以及 拓扑数据.
//for (size_t i = 0; i < 8; i++)
//{
// //随机点
// auto x = rm->GetRangeValue(-10,10);
// rm->Next();
// auto y = rm->GetRangeValue(-10, 10);
// rm->Next();
// auto z = rm->GetRangeValue(-10, 10);
// rm->Next();
// std::array<double, 3> curTempValue{x,y,z};
// mPointSource.emplace_back(curTempValue);
//}
//将原始的数据,设计成一条折线.
mPointSource.emplace_back(std::array<double, 3>{0,0,0});
mPointSource.emplace_back(std::array<double, 3>{10, -10, 0});
mPointSource.emplace_back(std::array<double, 3>{20, 10, 0});
mPointSource.emplace_back(std::array<double, 3>{30, -80, 0});
mPointSource.emplace_back(std::array<double, 3>{40, 12, 0});
mPointSource.emplace_back(std::array<double, 3>{80, 0, 0});2.2,具体创建过程:
2.2.1
FindClosestPoint () 我们先看这个函数的效果.
vtkNew<vtkPoints> mVtkPs;
vtkNew<vtkCellArray> mTopoCells;
for (auto& item : mPointSource)
{
mVtkPs->InsertNextPoint(item[0], item[1], item[2]);
}
//连接线.
auto cutPNumber = mVtkPs->GetNumberOfPoints();
for (size_t i = 1; i < cutPNumber; i++)
{
vtkNew<vtkLine> curLine;
curLine->GetPointIds()->SetId(0, i-1);
curLine->GetPointIds()->SetId(1, i);
mTopoCells->InsertNextCell(curLine);
}
vtkNew<vtkPolyData> mPolydata;
mPolydata->SetPoints(mVtkPs);
mPolydata->SetLines(mTopoCells);
//显示原始对象.
auto mActor = VtkCreatorHelper::CreateActorFromInputData(mPolydata);
mRender->AddActor(mActor);
//显示点.
vtkNew<vtkPolyData> mPointPolydata;
mPointPolydata->ShallowCopy(mPolydata);
auto mPointActor = VtkCreatorHelper::CreateActorFromInputData(mPointPolydata);
mPointActor->GetProperty()->SetPointSize(4);
mPointActor->GetProperty()->SetColor(0,1.0,0);
mPointActor->GetProperty()->SetRepresentationToPoints();
mRender->AddActor(mPointActor);
auto printPoint = [=](std::string str, double* value) {
std::cout << str.c_str() << " " << value[0] << " " << value[1] << " " << value[2] << std::endl;
};
switch (locatorType)
{
case 0:
{
//获取最近的距离...并将这个距离显示成
{
vtkNew<vtkPointLocator> mPointLocator; //使用点查询....
mPointLocator->SetDataSet(mPolydata);
mPointLocator->BuildLocator();
mPointLocator->Update();
VtkCreatorHelper::PrintVtkObjectInfo(mPointLocator);//输出.
auto outFilterActor = VtkCreatorHelper::CreateActorFromBounds(mPointLocator->GetBounds());
mRender->AddActor(outFilterActor);
//查询一.
int searchType = 1;
switch (searchType)
{
case 0:
{
//查询单独的点.
double testP[3]{ 20, 5, 0 };//20, 10, 0 1,2,3
auto findID = mPointLocator->FindClosestPoint(testP);
if (findID != -1)
{
auto findP = mPolydata->GetPoint(findID);
printPoint("要查的点 : ", testP);
printPoint("查找到的点: ", findP);
auto findActor = VtkCreatorHelper::CreateVtkSphereSource(findP[0], findP[1], findP[2], 3, 1.0, 1.0, 1.0, 0.6);
mRender->AddActor(findActor);
}
break;
}
该显示效果.
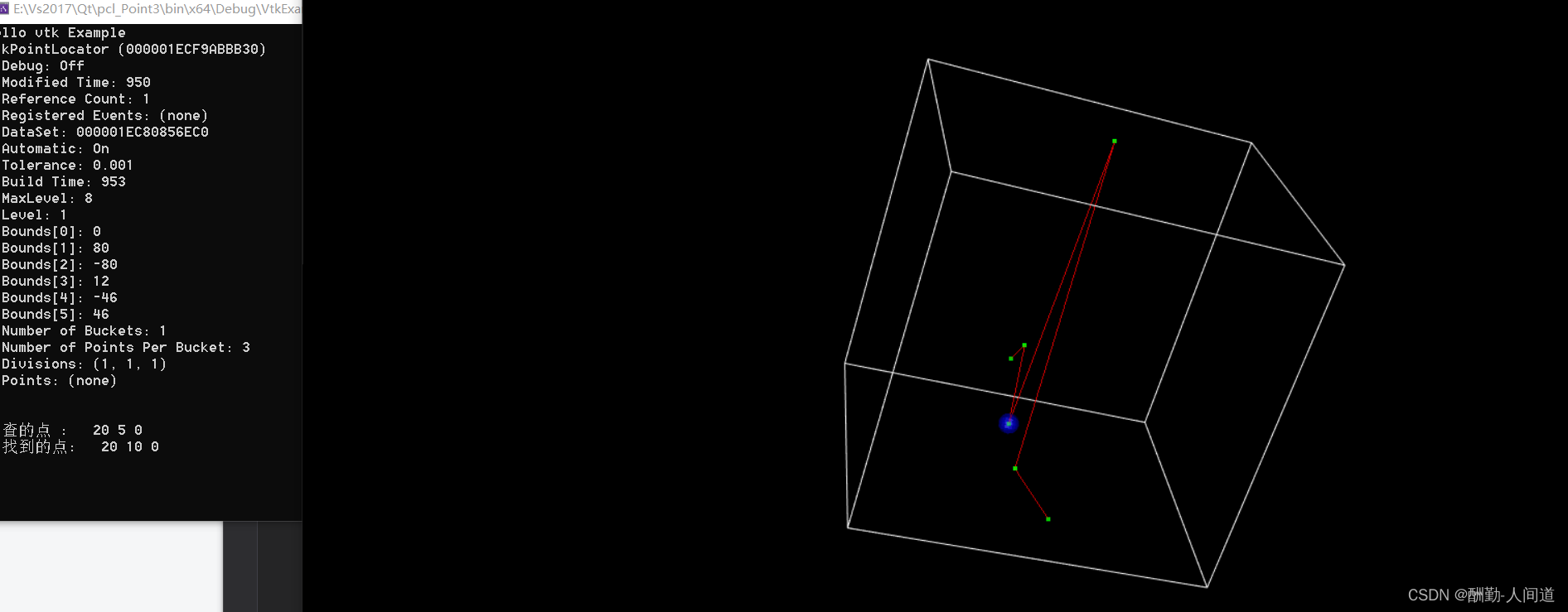
2.2.2
FindPointsWithinRadius() 我们再来看这个函数的效果. 注意这里的半径,以及搜索列表写法.
case 1:
{
//按照半径,查询
double testP[3]{ 20, 5, 0 };
printPoint("要查的点 : ", testP);
double R = 20;
vtkNew<vtkIdList> mList;
mPointLocator->FindPointsWithinRadius(R, testP, mList);
//绘制R为半径的圆.
auto RActor = VtkCreatorHelper::CreateVtkSphereSource(testP[0], testP[1], testP[2], R, 1.0, 1.0, 1.0, 0.3);
mRender->AddActor(RActor);
auto getPointsNumber = mList->GetNumberOfIds();
for (size_t i = 0; i < getPointsNumber; i++)
{
auto findP = mPolydata->GetPoint(mList->GetId(i));
printPoint("查找到的点: ", findP);
auto findActor = VtkCreatorHelper::CreateVtkSphereSource(findP[0], findP[1], findP[2], 3, 0.0, 0.0, 1.0);
mRender->AddActor(findActor);
}
break;
}
2.2.3 其他的函数使用方式,都和上面 两种方式一个样子,这里改出他们的理解
case 2:
{
//mPointLocator->FindClosestPointWithinRadius(); 这个本身就是在 Radius内部,查询众多点中,距离目标TestPoint最近的点.
break;
}
case 3:
{
//mPointLocator->FindClosestInsertedPoint(); 寻找插入点,最近的点.
break;
}2.2.4 特殊的一种巡点方式,是分布式.这个理解起来比较啰嗦. 我这里给出解释.
case 4:
{
//mPointLocator->FindDistributedPoints();
//这个没理解.仔细看一下: 这个函数是在分布式下进行查点搜寻的. 加快搜索速度,注意,结构必须也是 vtkDistributedDataSet 类型.
/*
需要注意的是,FindDistributedPoints 函数需要满足一定的条件才能使用。具体来说,要使用 FindDistributedPoints 函数,需要满足以下条件:
数据集必须是 vtkDistributedDataSet 类型。
数据集必须被正确地分割成多个部分,并且每个部分都被正确地分配给了不同的计算节点。
数据集的每个部分必须包含一个 vtkPointSet,并且这些 vtkPointSet 必须包含完整的点坐标信息。
如果满足以上条件,就可以在分布式计算环境中使用 FindDistributedPoints 函数进行点集操作了。
*/
}希望能帮助一些想要学习vtk的小伙伴



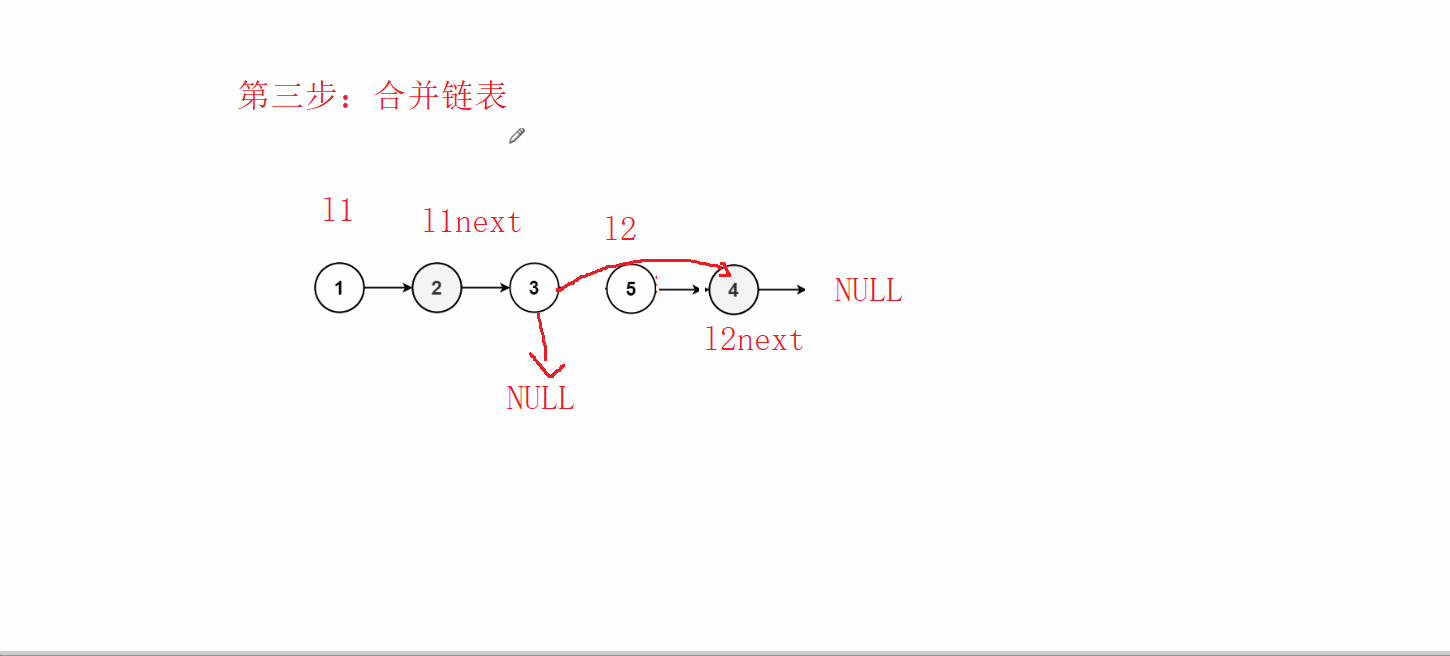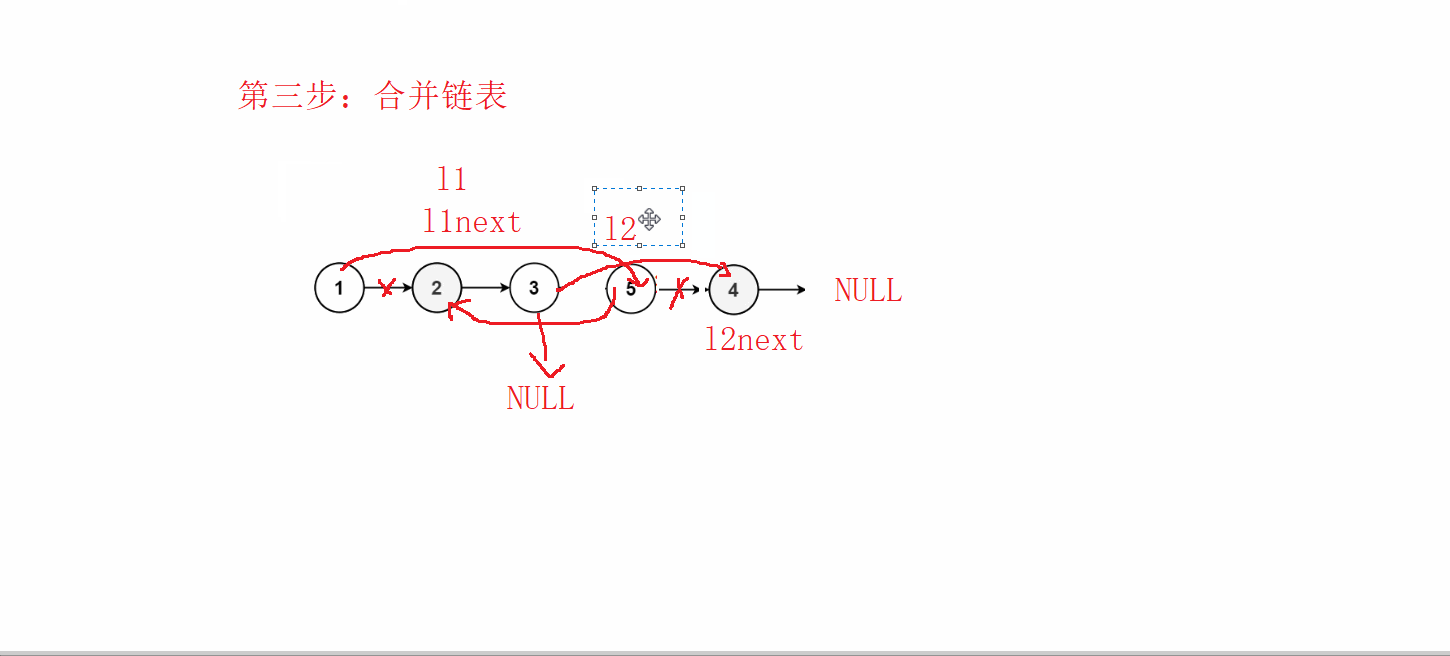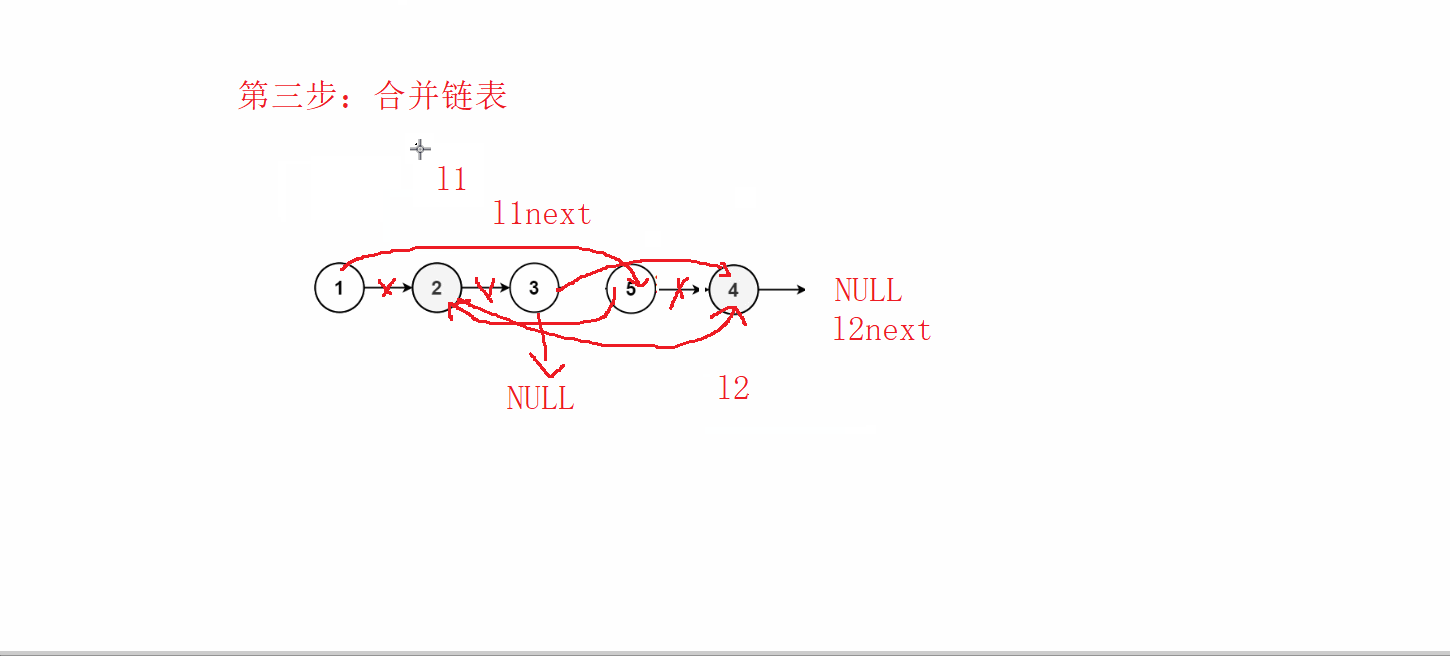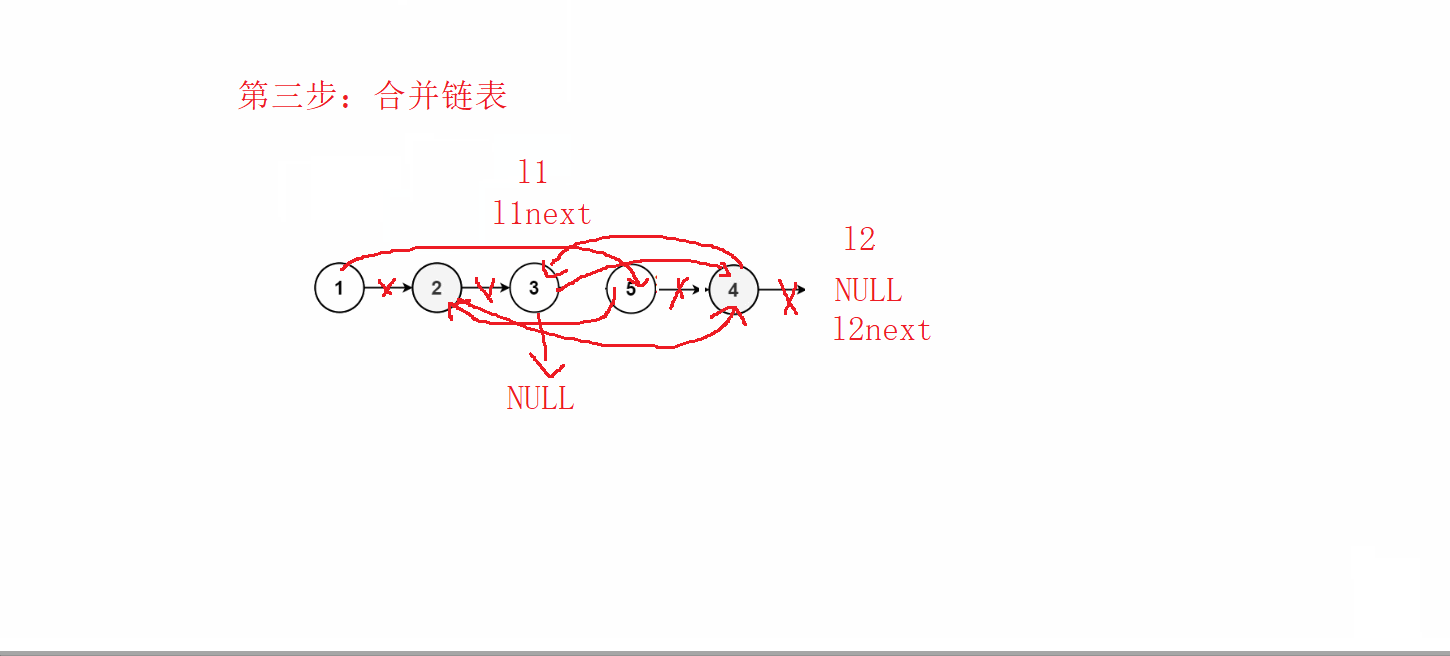

![shell文件通配符:任意一个:?、任意数量:*、任意包含[]、[^]:任意不包含](https://img-blog.csdnimg.cn/1444031bf1ad4b23858cecb12fc3d275.png)