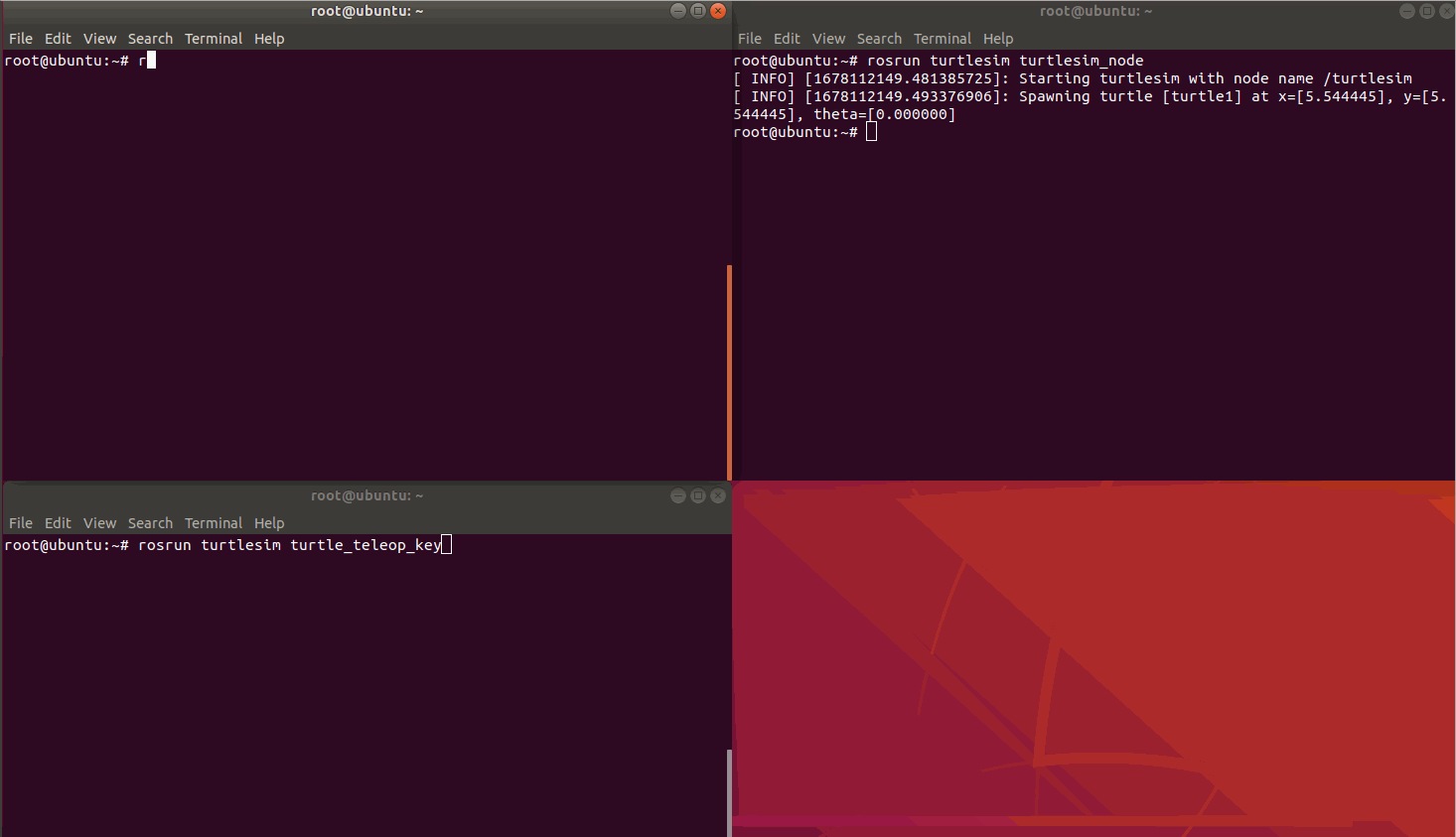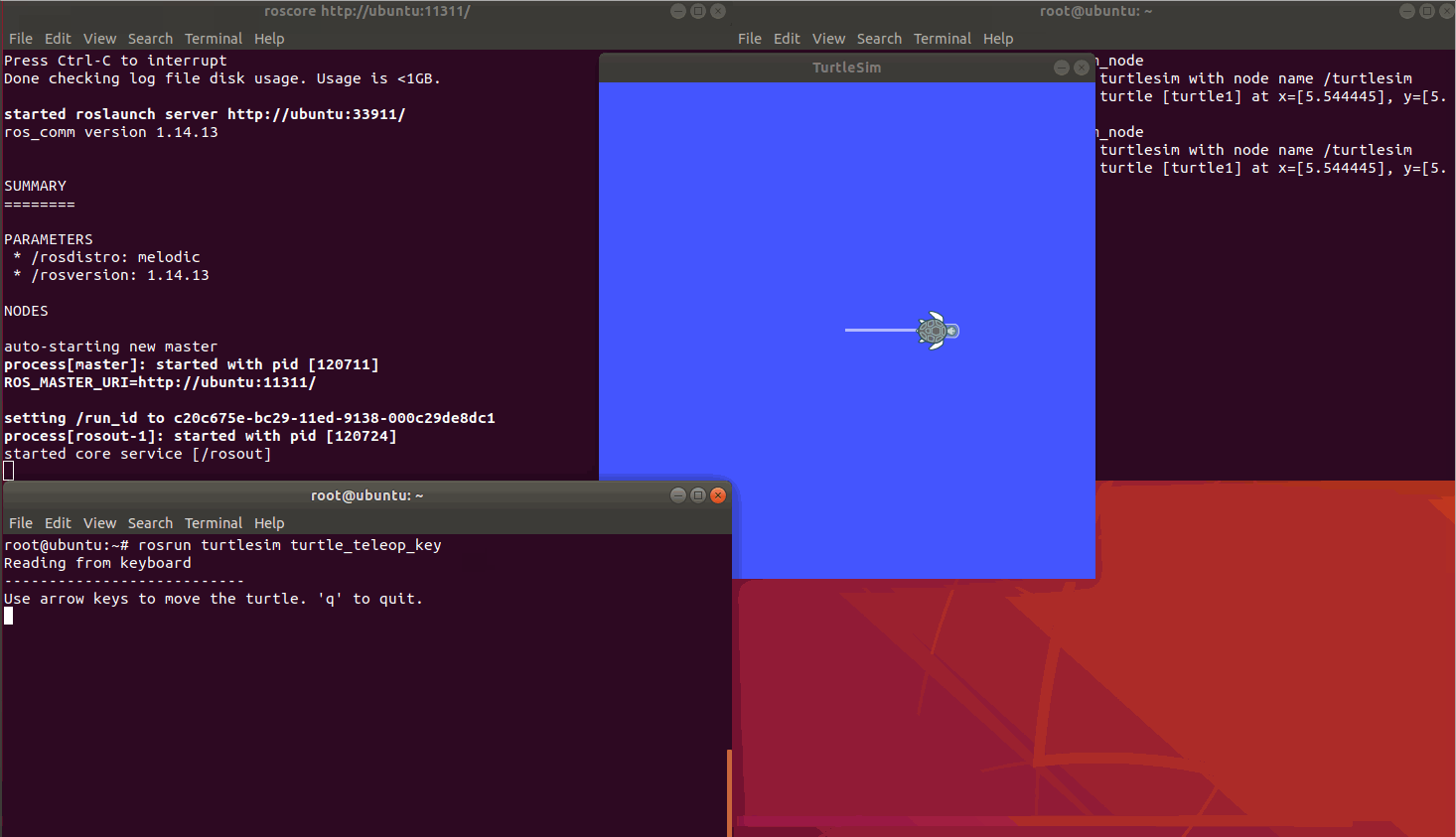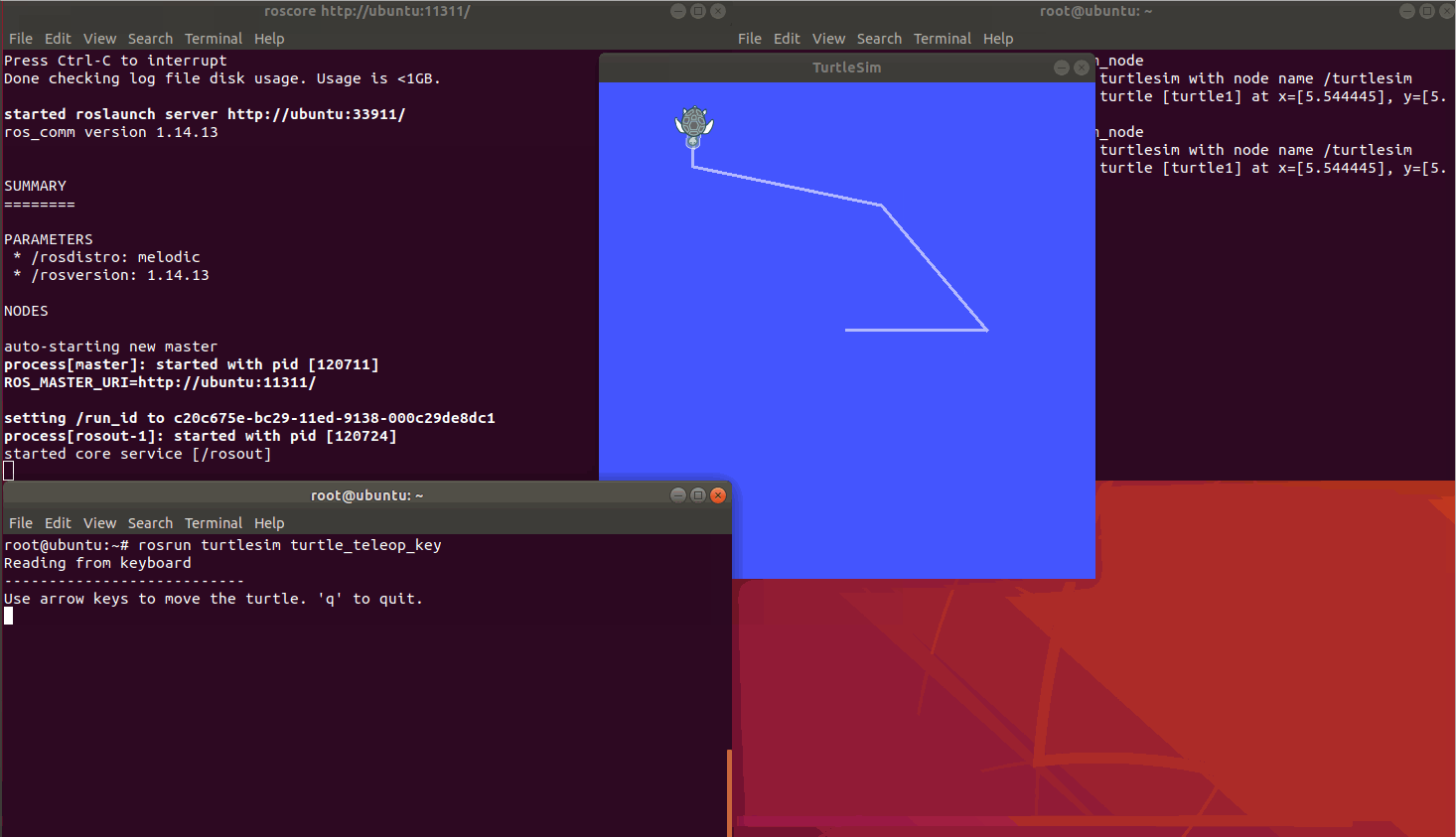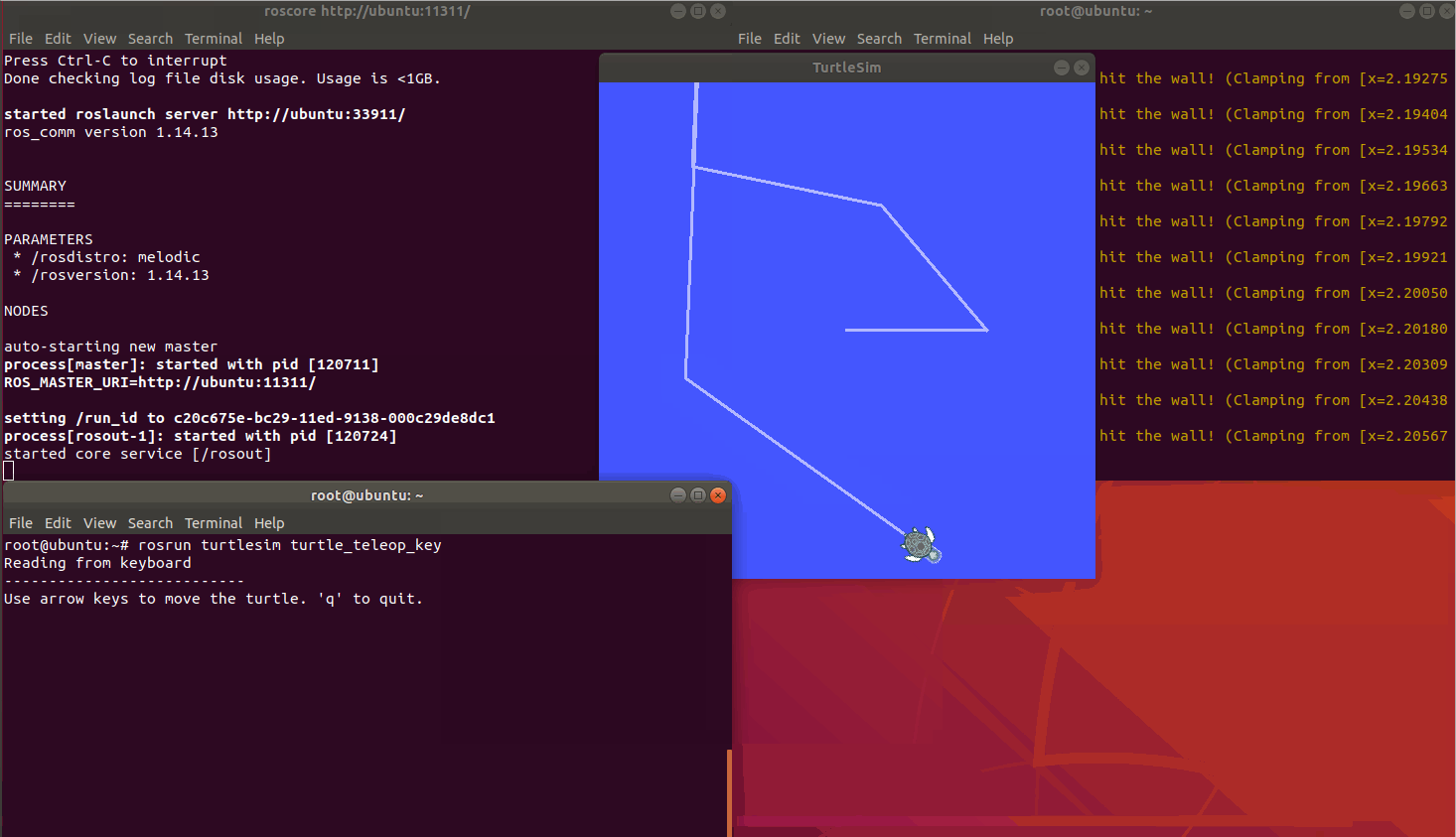
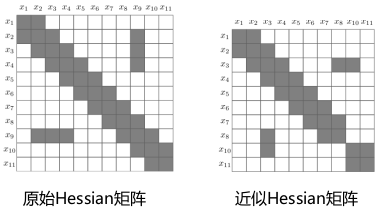
分治法的基本思想是将一个规模为n的问题分解为化个规模较小的子问题，这些子问题互相独立且与原问题相同。递归地解这些子问题，然后将各子问题的解合并得到原问题的解。

它的一般的算法设计模式如下：

divide-and-conquer(P)
{
if ( P <= no)
adhoc(P):
divide P into smaller subinstances P1,P2,-, Pk;
for (i=1; i <= k; i++)
y = divide-and-conquer(Pi);
return merge (y1, y2, ., yk);
}

其中，P表示问题口的规模，n0为一阙值，表示当问题口 的规模不超过 n0时，问题容易解出，

不必再继续分解。adhoc(D)是该分治法中的基本子算法，用于直接解小规模的问题P。当P的规

模不超过n0 时，直接用算法 adhoc(P)求解。算法 merge(y1, y2,•，yK)是该分治法中的合并子算

法，用于将P的子问题P1,P2,⋯，PK的解y1，y2，，水合并为『的解。

根据分治法的分割原则，应把原问题分为多少个子问题才较适宜？每个子问题是否规模

相同或怎样才为适当？这些问题很难予以肯定回答。但人们从大量实践中发现，在用分治法

设计算法时，最好使子问题的规模大致相同，即将一个问题分成大小相等的么个子问题的处

理方法是行之有效的。许多问题可以取人=2。这种使子问题规模大致相等的做法出自一种平

衡 （balancing）子问题的思想，几乎总是比子问题规模不等的做法要好。从分治法的一般设计模式可以看出，用它设计出的程序一般是递归算法，因此分治法的计算效率通常可以用递归方程来进行分析。一个分治法将规模为n的问题分成n个规模为 nlim的子问题去解。为方便起见，设分解國值n0为1，且adhoc 解规模为1的问题耗费 1单位时间。另外，将原问题分解为么个子问题及用merge将后个子问题的解合并为原问题的解需用

£n)单位时间。如果用7（n)表示该分治法 divide-and-conquer(P)解规模为P=n 的问题所需的计

反思：

我的疑惑：

T(N)是如何求出来的呢？

即递归方程怎么解？就是接下来任务的重点。