二叉树的构造：没有中序遍历则无法唯一构造

1.二叉树的遍历

2.二叉树的构造

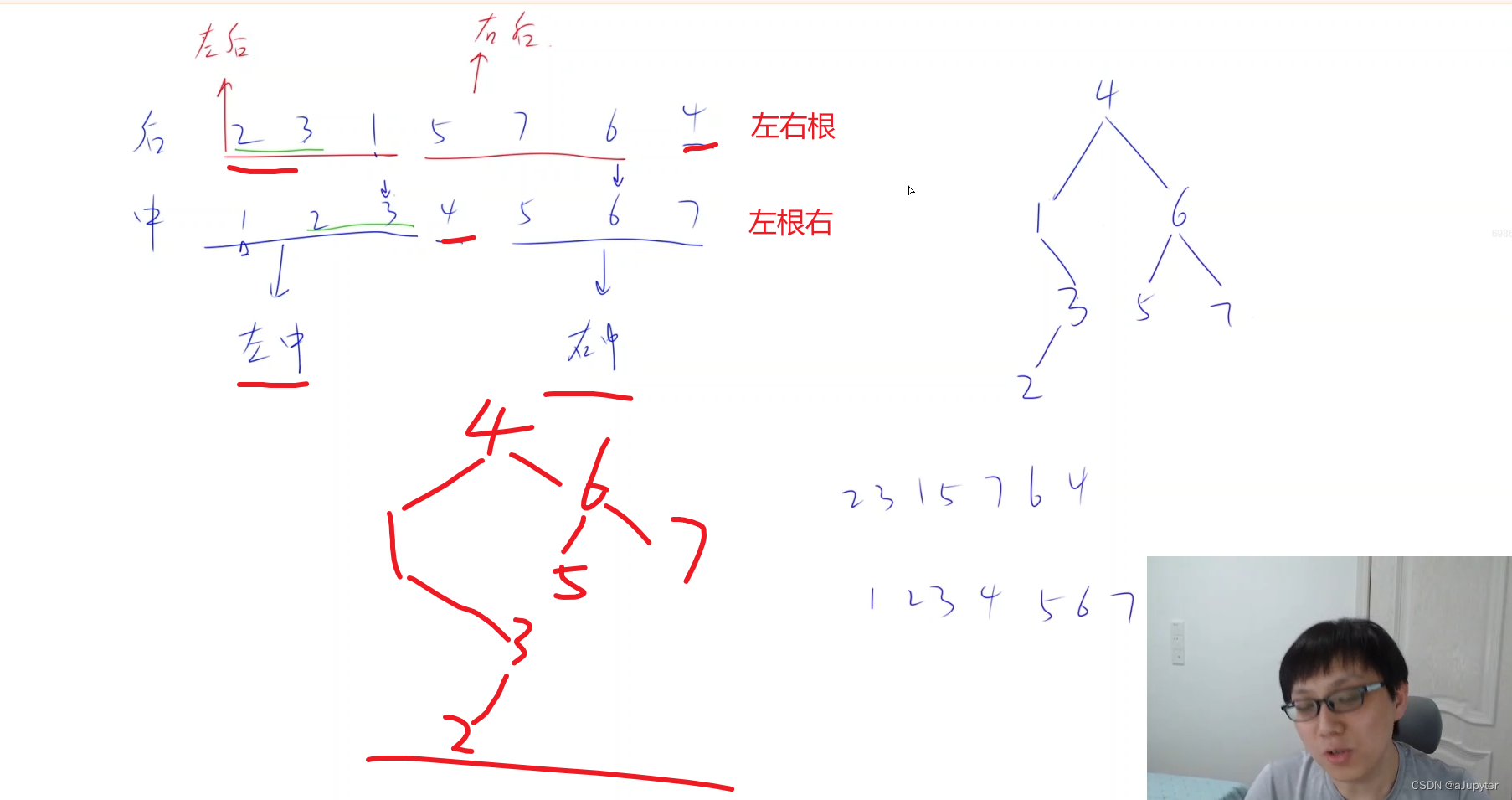
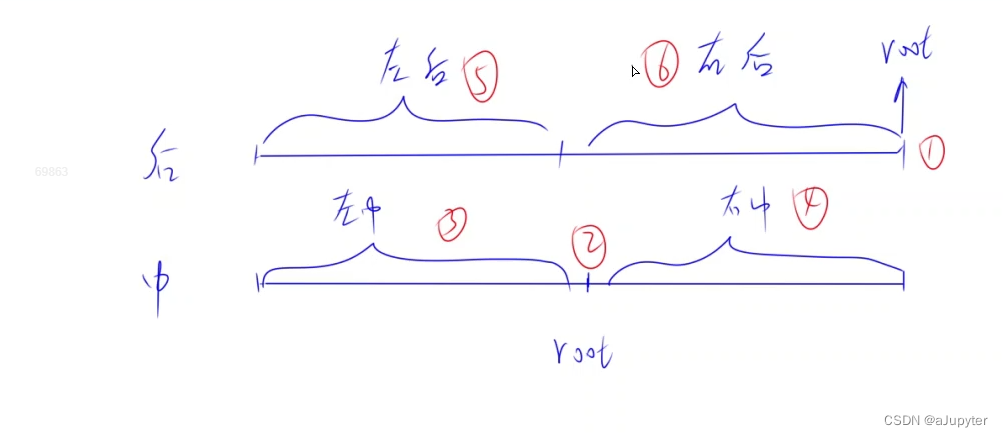
3.例题

一个二叉树，树中每个节点的权值互不相同。

现在给出它的后序遍历和中序遍历，请你输出它的层序遍历。

输入格式
第一行包含整数 N
，表示二叉树的节点数。

第二行包含 N
个整数，表示二叉树的后序遍历。

第三行包含 N
个整数，表示二叉树的中序遍历。

输出格式
输出一行 N
个整数，表示二叉树的层序遍历。

数据范围
1≤N≤30
,
官方并未给出各节点权值的取值范围，为方便起见，在本网站范围取为 1∼N
。

输入样例：
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7
输出样例：
4 1 6 3 5 7 2

3.1不使用BFS

#include <iostream>
#include <vector>

using namespace std;
const int N = 35;

int a[N], b[N], p[N];

vector<int> level[N];

void build(int al, int ar, int bl, int br, int d)
{
    if(al > ar) return;
    int val = a[ar]; // 根节点
    level[d].push_back(val);
    int k = p[val]; // 根节点的下标
    build(al,al + k - 1 - bl , bl, k - 1, d + 1); // 左子树
    build(al + k - bl, ar - 1, k + 1, br, d + 1);
}

int main()
{
    int n;
    cin >> n;
    for (int i = 0; i < n; i ++) cin >> a[i];
    for (int i = 0; i < n; i ++) cin >> b[i];
    for (int i = 0; i < n; i ++) p[b[i]] = i;
    
    build(0, n - 1, 0, n - 1, 0);
    
    for (int i = 0; i < n; i ++)
        for (auto x: level[i])
            cout << x << ' ';
    return 0;
    
}

3.2使用BFS

#include <iostream>
#include <queue>

using namespace std;

const int N = 35;
int a[N], b[N], p[N];
int l[N], r[N];
int n;

int build(int al, int ar, int bl, int br)
{
    if (al > ar) return 0;
    int val = a[ar];
    int k = p[val];
    
    l[val] = build(al, k - 1 - bl + al, bl, k - 1);
    r[val] = build(k - bl + al, ar - 1, k + 1, br);
    
    return val;
}

void bfs()
{
    queue<int> q;
    q.push(a[n - 1]); // 根节点入队
    while(q.size())
    {
        int t = q.front(); // 队首
        q.pop(); // 删除队首
        cout << t << ' ';
        if (l[t]) q.push(l[t]); // 左孩子
        if (r[t]) q.push(r[t]); // 右孩子
    }
}
int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++) cin >> a[i];
    for (int i = 0; i < n; i ++) cin >> b[i];
    for (int i = 0; i < n ; i ++) p[b[i]] = i;
    
    build(0, n - 1, 0, n - 1);
    
    bfs();
    return 0;
}