蓝桥杯训练day2

news2024/9/23 7:27:54

day2

  • 1.二分
    • (1)789. 数的范围
    • (2)四平方和
      • （1）哈希表做法
      • （2）二分做法
    • (3)1227. 分巧克力
    • （4）113. 特殊排序
    • (5)1460. 我在哪？
  • 2.双指针
    • (1)1238. 日志统计
    • (2)1240. 完全二叉树的权值
    • （3）字符串删减
    • (4)799. 最长连续不重复子序列
    • (5)800. 数组元素的目标和
    • (6)判断子序列

1.二分

(1)789. 数的范围

在这里插入图片描述

思路：
需要找到一个值的区间。比如1 2 2 3 4 5 找2的区间，即[1,2]
因为数组是有序的，所以可以使用二分查找。

(1)使用二分查找找左边界
(2)使用二分查找找右边界

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=100010;

int  n,q;
 
int a[N];

int find1(int t)  //找到当前查找数的区间左边界
{
    int res=-1;
    int l=0,r=n-1;
    int mid=(l+r)>>1;
    while(l<=r)
    {
        mid=(l+r)>>1;
        if(a[mid]>t)r=mid-1;
        else if(a[mid]<t)
            l=mid+1;
        else
        {
            res=mid;
            r=mid-1;
        }
    }
    return res;
}

int find2(int t)
{
    int res=-1;
    int l=0,r=n-1;
    int mid=(l+r)>>1;
    while(l<=r)
    {
        mid=(l+r)>>1;
        if(a[mid]>t)r=mid-1;
        else if(a[mid]<t)
            l=mid+1;
        else
        {
            res=mid;
            l=mid+1;
        }
    }
    return res;
}


int main()
{
    cin>>n>>q;
    for(int i=0;i<n;i++)
        cin>>a[i];
    while(q--)
    {
        int t;
        cin>>t;
        cout<<find1(t)<<" "<<find2(t)<<endl;
    }
    return 0;
}

(2)四平方和

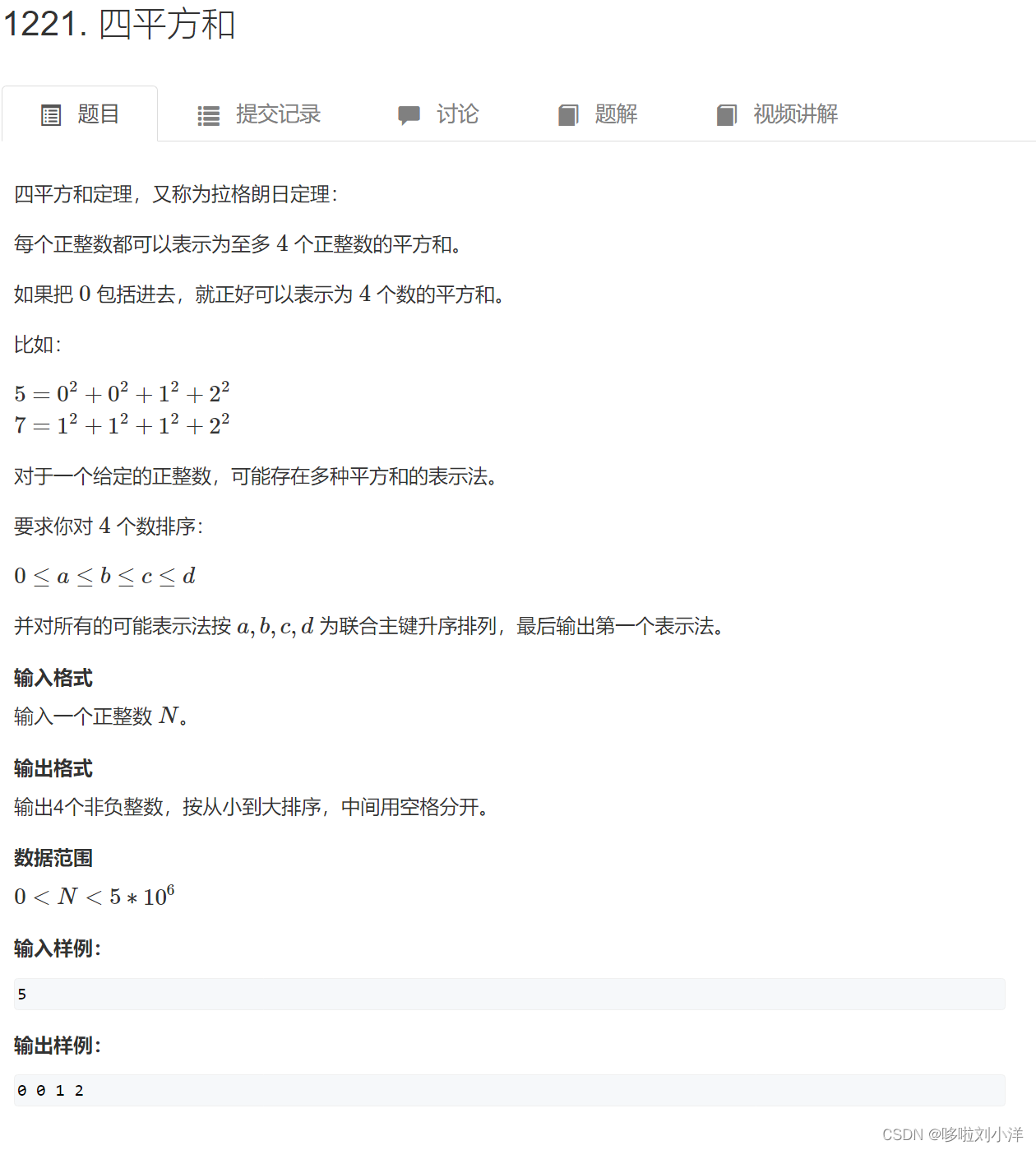
在这里插入图片描述

经典哈希问题，二分问题。
第一步：先找出两个数的平方和的所有组合（不超过n）
第二步：n减去两个数的平方和，剩下的数看是否在第一步预处理过。

为什么可以保证字典序最小呢：
（1）在第二步中，a，b是从小到大枚举的，且可以保证a<=b恒成立，为什么？如果a>b成立，那么把a，b置换一下，一样成立。然后第一次成立就会结束，所以不可能遇到a>b的情况

(2)C[k],D[k]也是一样的道理。在第一步就可以证明。

（1）哈希表做法

#include<iostream>
#include<cstring>
using namespace std;

const int N=5000010;

int C[N],D[N];

int n;

int main()
{
    cin>>n;
    memset(C,-1,sizeof C);
    //第一步：将所有两个数的组合都算出来
    for(int a=0;a*a<=n;a++)
    {
        for(int b=a;b*b+a*a<=n;b++)
        {
            int k=a*a+b*b;
            if(C[k]==-1)
            {
                C[k]=a,D[k]=b;
            }
        }
    }
    
    //第二步，将n减去ab两个数的组合，剩下的看之前是否存储，如果有，直接输出。而且一定满足字典序最小
    
    for(int a=0;a*a<=n;a++)
    {
        for(int b=a;b*b+a*a<=n;b++)
        {
            int k=n-a*a-b*b;
            if(C[k]!=-1)
            {
                cout<<a<<" "<<b<<" "<<C[k]<<" "<<D[k]<<endl;
                return 0;
            }
        }
    }
    return 0;
    
}

（2）二分做法

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=5000010;

struct Sum
{
    int s,c,d;   //s表示a*a+b*b
    bool operator<(const Sum &t)const   //为什么重载小于号
    {
        if(s!=t.s)return s<t.s;
        if(c!=t.c)return c<t.c;
        return d<t.d;
    }
}sum[N];


int n;
int m;

int main()
{
    cin>>n;
    for(int c=0;c*c<=n;c++)
        for(int d=c;c*c+d*d<=n;d++)
            sum[m++]={c*c+d*d,c,d};
            
    sort(sum,sum+m);
    
    for(int a=0;a*a<=n;a++)
    {
        for(int b=a;b*b+a*a<=n;b++)
        {
            int t=n-a*a-b*b;
            int l=0,r=m-1;
            while(l<r)
            {
                int mid=(l+r)>>1;
                if(t<=sum[mid].s)
                    r=mid;
                else
                    l=mid+1;
            }
            if(t==sum[l].s)  //或者t==sum[r].s  因为最终l==r
            {
                cout<<a<<" "<<b<<" "<<sum[r].c<<" "<<sum[r].d<<endl;
                return 0;
            }
        }
        
    }
    return 0;
}

(3)1227. 分巧克力

在这里插入图片描述

还以为有什么技巧咧，看半天。。就一个暴力做法。。。二分正方形的边长

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=1e5+10;

int n,k;

int H[N],W[N];


bool check(int t)
{
    long long res=0;
    for(int i=0;i<n;i++)
    {
        res+=H[i]/t*(W[i]/t);
        if(res>=k)return  true;
    }
    return false;
}
int main()
{
    cin>>n>>k;
    for(int i=0;i<n;i++)
        cin>>H[i]>>W[i];
        
    int l=1,r=1e5;
    while(l<r)
    {
        int mid=(l+r+1)>>1;   //为什么+1，这是因为避免死循环，为什么会死循环。博客里面有相关文章
        if(check(mid))l=mid;
        else
            r=mid-1;
    }
    
    cout<<l<<endl;
    return 0;
}

（4）113. 特殊排序

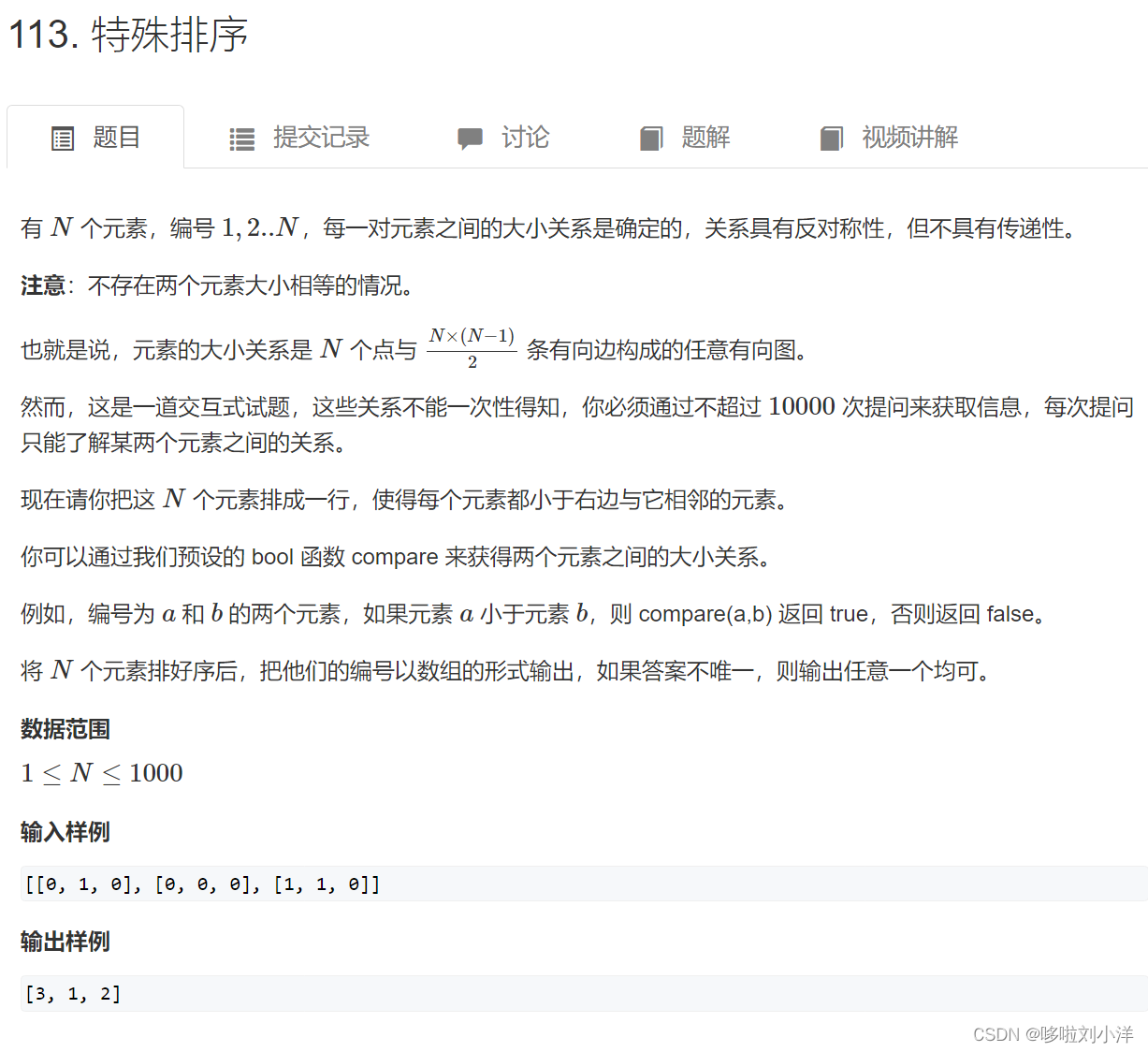
在这里插入图片描述

难难难！！!
关键在于对“无序二分”的合理证明。
二分一定是有道理才能的。光看难懂，要仔细体会。不会的小伙伴可以私信，我这个菜鸟看了30分钟才看懂😢

// Forward declaration of compare API.
// bool compare(int a, int b);
// return bool means whether a is less than b.

class Solution 
{
public:
    vector<int> specialSort(int N) 
    {
        vector<int>res;
        res.push_back(1);    //使用插入排序+二分，res就是排序主体，开始数组只有1个元素，当然是有序的
        for(int i=2;i<=N;i++)
        {
            //这里规定找到第一个小于i的位置，且该位置后面一个数大于i。然后让i插入到第一个小于i的位置后面的一个位置
            //这是合理的.
            //如果当前数x比i小，那么i一定可以在x右边放下：如果x右边所有的数都比i小，那么i放在最右端
            //如果x右边有一个数比i大，那么i放在该数位置，该数以及后面的数右移。
            //所以找到第一个小于i的数且后面大于i的数（也可以没有）即可
            //注意，如果没有小于i的数，那么i放在第一位
            int l=0,r=res.size()-1;
            
            while(l<r)
            {
                int mid=(l+r+1)>>1;
                if(compare(res[mid],i))l=mid;   //如果mid小于i，那么i一定可以插入到mid后面(也可能可以插入到mid左边)
                else
                    r=mid-1;
            }
            res.push_back(i);
            //最后l==r，[l，l+1]分别表示小于i，大于i的数
            for(int j=res.size()-2;j>r;j--)
                swap(res[j],res[j+1]);
                
            //判断r是否合理。如果i比res[r]小，则和我们假设不符合，那么就只有一种可能，i比所有数都小，自然也比第一个数小，这个时候i只可能是第二个数，那么和第一个数交换位置即可
            if(compare(i,res[r]))swap(res[r],res[r+1]);
            //也可写 if(compare(res[r+1],res[r])swap(res[r],res[r+1]);
            
        }
   
        return res;
        
    }
};

(5)1460. 我在哪？

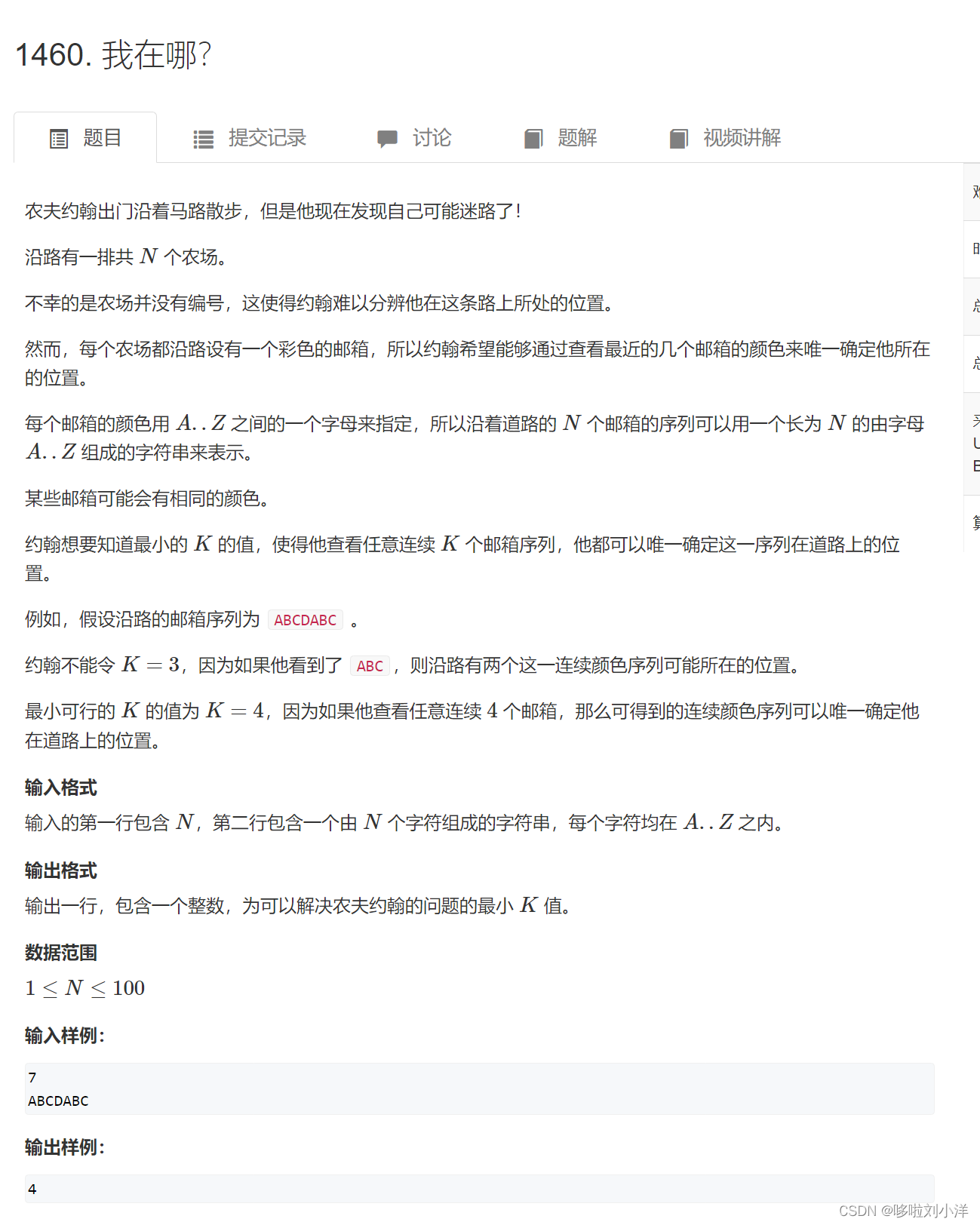
在这里插入图片描述

这道题数据很小，可以直接暴力解决。直接枚举所有连续的字符串的组合，找到唯一的那一个，记录下长度即可，非常简单。但是标签是二分，待我去看看题解如何解答。。

//目的找到一个最小长度且没有重复的字符串

#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using  namespace std;

const int N=110;

int n;
char str[N];
int res;


int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>str[i];
        
    unordered_map<string,int>Hash;
    for(int len=1;len<=n;len++)  //枚举长度
    {
        int cnt=0;
        for(int start=1;start+len-1<=n;start++)  //枚举起点
        {
            string temp="";
            for(int j=start;j<=start+len-1;j++)  //累计枚举区间的字符串
                temp+=str[j];
            Hash[temp]++;
            if(Hash[temp]==1)cnt++;
        }
        if(cnt==n-len+1)  //说明该长度的所有组合都是第一次出现
        {
            cout<<len<<endl;
            return 0;
        }
    }
    return
    
}

二分还真可以做，需要字符串哈希的我知识，也可以直接用stl
先贴一个代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_set>

using namespace std;

int n;
string str;
unordered_set<string> S;

bool check(int mid)
{
    S.clear();
    for (int i = 0; i + mid - 1 < n; i ++ )
    {
        string s = str.substr(i, mid);
        if (S.count(s)) return false;
        S.insert(s);
    }

    return true;
}

int main()
{
    cin >> n >> str;

    int l = 1, r = n;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }

    cout << r << endl;

    return 0;
}

2.双指针

(1)1238. 日志统计

在这里插入图片描述

双指针的习题：
思路：先给排序，排序规则：帖子编号从小到大，如果帖子编号一样，则给时间从小到大排序

然后用一个l，r指向一个帖子的区间，判断该帖子是否满足要求，然后判断下一个帖子

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N = 1e5 + 10;

int n, d, k;

int res[N];
int rc=0;

struct node
{
    int id;
    int ts;
    node():id(0),ts(0){}
};

node a[N];


bool cmp(node &a, node& b)  
{
    if (a.id == b.id)return a.ts < b.ts;
    return a.id<b.id;
}


int main()
{
    cin >> n >> d >> k;
    for (int i = 0; i < n; i++)
        cin >> a[i].ts >> a[i].id;

    sort(a, a + n, cmp);
    // for (int i = 0; i < n; i++)
    // {
    //     cout << a[i].ts << " " << a[i].id << endl;
    // }
    
    //对帖子一个个进行判断
    //一个指针指向起始时间，一个指向末尾时间
    int l=0,r=0;  //l，r分别是一个帖子的不同时间(开始时间和截至时间)
    int cnt=0;
    while(l<n&&r<n)
    {
        if(a[l].id==a[r].id)  //帖子一样
        {
            if(a[r].ts-a[l].ts+1<=d)
            {
                cnt++;
                r++;
            }
            else
            {
                l++;
                cnt--;
            }
            if(cnt==k)
            {
                res[rc++]=a[l].id;
                cnt=0;
                int t=a[l].id;
                while(a[l].id==t)
                    l++;
                r=l;
            }
        }
        
        else
        {
            l=r;
            cnt=0;
        }
        
        
    }
    
    

    
    for(int i=0;i<rc;i++)
        cout<<res[i]<<endl;

    return 0;
}

(2)1240. 完全二叉树的权值

在这里插入图片描述
思路：
先将每一层的权值算出来，然后用一个变量res记录最大值。因为层数从小到大遍历，遇到大的才更新，所以可以保证第一次遇到的最大值层数最小。

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 100010;

int n;
int a[N];

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);

    LL maxs = -1e18;
    int depth = 0;

    for (int d = 1, i = 1; i <= n; i *= 2, d ++ )
    {
        LL s = 0;
        for (int j = i; j < i + (1 << d - 1) && j <= n; j ++ )
            s += a[j];
        
        cout<<s<<endl;
        if (s > maxs)
        {
            maxs = s;
            depth = d;
        }
    }

    printf("%d\n", depth);

    return 0;
}

贴上自己第一次写的代码，说明功底还不够

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=1e6+10;

ll a[N];
ll deep[N];  //deep[i]=j表示深度为i的那一层的权值之和为j
int dc=1;

int n;


struct node
{
    int d;
    ll cnt;
};

node b[N];

bool cmp(node &a,node &b)
{
    if(a.cnt==b.cnt)return a.d<b.d;
    return a.cnt>b.cnt;
    
}

void count()  //计算每一层的个数
{
    int start=0; //一层的开始
    int k=1;  //一层的个数
    while(start<=n)   //计算每一层的权值
    { 
        for(int i=start;i<min(n,start+k);i++)
        {
           deep[dc]+=a[i];
        }
        start+=k;
        k*=2;
        dc++;
    }
}


int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>a[i];
    
    count();
    
    // for(int i=1;i<dc;i++)
    //     cout<<deep[i]<<" ";
    
    //将每一层的权值之和都算出来就简单了，想怎么做都可以,用一个结构体存下层数和大小，先按大小排序，
    //cout<<dc<<endl;
    //如果大小一样，就按照层数排序
    for(int i=1;i<dc;i++)
    {
        b[i].d=i;
        b[i].cnt=deep[i];
    }
    sort(b+1,b+dc,cmp);
    
    cout<<b[1].d<<endl;
    
    return 0;
    
}

（3）字符串删减

在这里插入图片描述

思路：
准备工作：
（1）变量ok，遇到x置为true，否则false
（2）left，right指针，left指向第一个遇到的x，right指向最后一个遇到的x

一次遍历即可

#include<iostream>
#include<cstring>

using namespace std;



const int N=110;

int n;
char a[N];
int res=0;


int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>a[i];
       
    int l,r;
    int sum=0;
    bool ok=false;
    for(int i=0;i<n;i++)
    {
        if(a[i]=='x')
        {
            if(!ok)
            {
                l=r=i;
                sum=1;
                ok=true;
            }
            else
            {
                r++;
                sum++;
            }
        }
        else
        {
            ok=false;
            if(sum>=3)
            {
                res+=sum-2;
                sum=0;
            }
        }
    }
    if(sum>=3)res+=sum-2;
    cout<<res<<endl;
    return 0;
    
}

(4)799. 最长连续不重复子序列

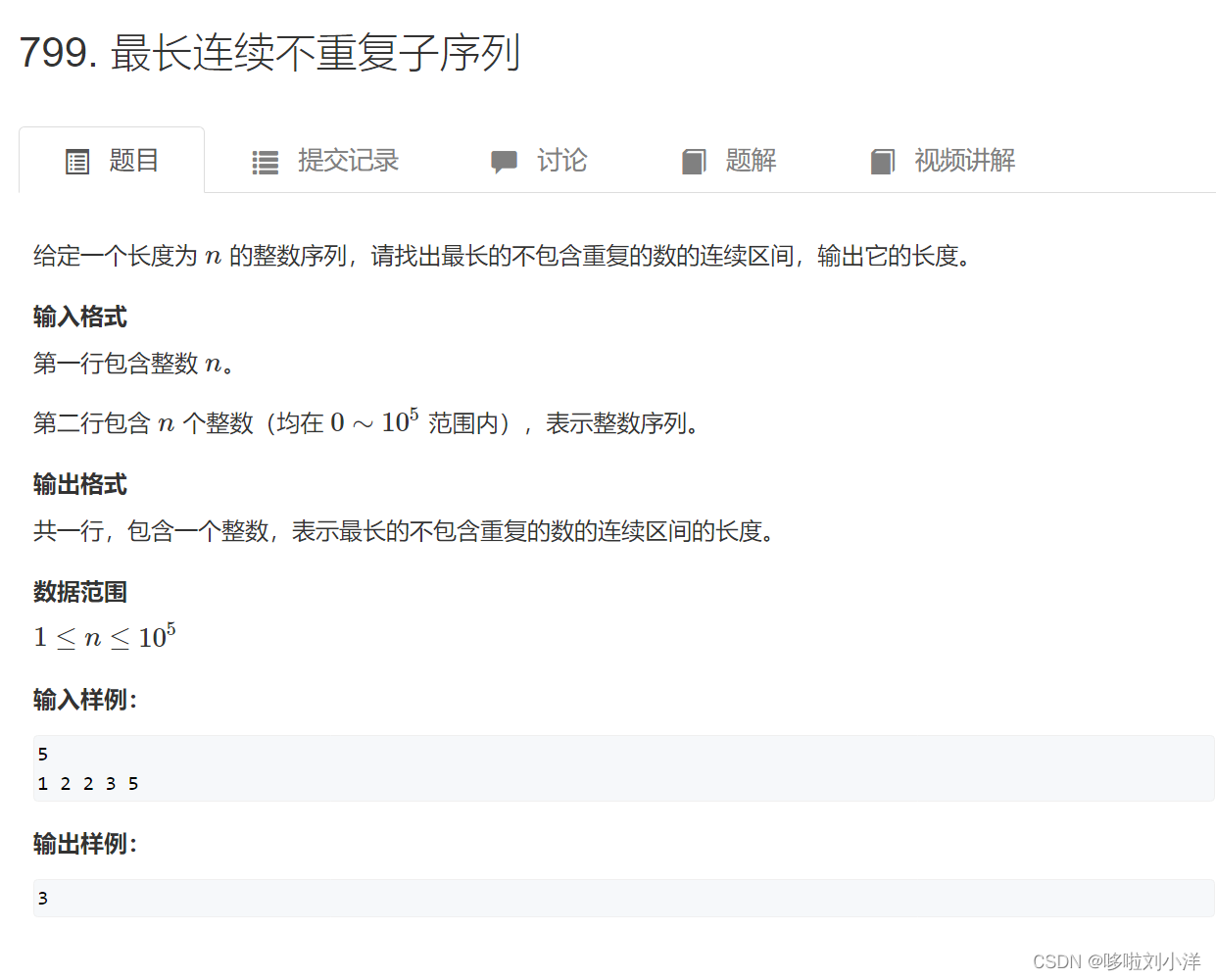
在这里插入图片描述
用一个哈希表实时记录出现的元素次数，两个指针指向前后一次遍历即可

#include<iostream>
#include<cstring>
#include<algorithm>
#include<unordered_map>
using namespace std;


const int N = 1e5 + 10;

int a[N];
int n;

int res = 0;

int main()
{
    cin >> n;
    for (int i = 0; i < n; i++)
        cin >> a[i];

    unordered_map<int, int>Hash;  //哈希表

    int l = 0, r = 0;

    while (l < n && r < n)
    {
        if (Hash.count(a[r]) == 0 || Hash[a[r]] == 0)
        {
            Hash[a[r]] = 1;
            r++;
        }
        else
        {
            res = max(res, r - l);
            while (l < n && a[l] != a[r])
            {
                Hash[a[l]] = 0;
                l++;
            }
            Hash[a[l]] = 0;
            l++;
        }
    }
    res=max(res,r-l);  //最后一次判断，以免漏掉
    cout << res;
    return 0;

}

(5)800. 数组元素的目标和

在这里插入图片描述

经典双指针，一前一后。用反证法证明不会漏过答案

#include<iostream>
#include<cstring>
using namespace std;


const int N=1e5+10;

int a[N];
int b[N];

int n,m;
int k;

int main()
{
    cin>>n>>m>>k;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    for(int j=1;j<=m;j++)
        cin>>b[j];
    
    int l=1,r=m;
    bool ok=true;
    while(ok)
    {
        if(a[l]+b[r]>k)
            r--;
        else if(a[l]+b[r]<k)
            l++;
        else
            ok=false;
    }
    cout<<l-1<<" "<<r-1<<endl;
    return 0;
    
}

(6)判断子序列

在这里插入图片描述

#include<iostream>
#include<cstring>
using namespace std;

const int N=1e5+10;

int n,m;

int a[N],b[N];

int main()
{
    cin>>n>>m;
    
    for(int i=0;i<n;i++)
        cin>>a[i];
    for(int i=0;i<m;i++)
        cin>>b[i];
    int i,j;
    for(i=0,j=0;i<n&&j<m;j++)
    {
        if(a[i]==b[j])
            i++;
    }
    
    if(i==n)cout<<"Yes";
    else    cout<<"No";
    
    
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/392576.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

koa-vue的分页实现

koa-vue的分页实现

1.引言 最近确实体会到了前端找工作的难处&#xff0c;不过大家还是要稳住心态&#xff0c;毕竟有一些前端大神说的有道理&#xff0c;前端发展了近20年&#xff0c;诞生了很多leader级别的大神&#xff0c;这些大神可能都没有合适的坑位&#xff0c;我们新手入坑自然难一些&am…
阅读更多...
HD-G2L-IOT V2.0核心板MPU压力测试

HD-G2L-IOT V2.0核心板MPU压力测试

1. 测试对象HD-G2L-IOT基于HD-G2L-CORE V2.0工业级核心板设计&#xff0c;双路千兆网口、双路CAN-bus、2路RS-232、2路RS-485、DSI、LCD、4G/5G、WiFi、CSI摄像头接口等&#xff0c;接口丰富&#xff0c;适用于工业现场应用需求&#xff0c;亦方便用户评估核心板及CPU的性能。H…
阅读更多...
PMP高分上岸人士的备考心得，分享考试中你还不知道的小秘密

PMP高分上岸人士的备考心得，分享考试中你还不知道的小秘密

上岸其实也不是什么特别难的事情&#xff0c;考试一共就180道选择题&#xff0c;题目只要答对60.57%就可以通过考试&#xff0c;高分通过没在怕的&#xff0c;加油备考呀朋友们&#xff01; 这里也提一嘴&#xff0c;大家备考的时候比较顾虑的一个问题就是考试究竟要不要报班…
阅读更多...
js循环判断的方法

js循环判断的方法

js循环判断的方法if语句if else语句if else if else if......三元表达式switchswitch语句和if语句的区别for循环while循环do while循环for inforEachfor of性能问题if语句 条件满足就执行&#xff0c;不满足就不执行 if(条件){语句}if else语句 条件满足&#xff0c;执行语句…
阅读更多...
认识3D旋转变换矩阵

认识3D旋转变换矩阵

前文输出了cesium的Rotation变量&#xff0c;一个矩阵&#xff1b;把这矩阵写下来看下&#xff1b; 0.99939 -0.034899 0 0 0.034899 0.99939 0 0 0 0 1 0 0 0 0 1 看一下3D数学的相关描述&#xff1b;…
阅读更多...
周赛335（模拟、质因子分解、分组背包）

周赛335（模拟、质因子分解、分组背包）

题解&#xff1a;0x3f https://leetcode.cn/problems/number-of-ways-to-earn-points/solution/fen-zu-bei-bao-pythonjavacgo-by-endlessc-ludl/ 文章目录周赛335[6307. 递枕头](https://leetcode.cn/problems/pass-the-pillow/)模拟[6308. 二叉树中的第 K 大层和](https://le…
阅读更多...
扬帆优配|本周限售股解禁规模不足300亿元，这8家公司解禁压力大

扬帆优配|本周限售股解禁规模不足300亿元，这8家公司解禁压力大

本周限售股解禁规模环比大降至300亿元之下。 Wind数据显示&#xff0c;除掉新上市公司&#xff0c;本周A股商场共有36家公司限售股解禁&#xff0c;解禁数量27.69亿股&#xff0c;以最新收盘价核算&#xff08;下同&#xff09;&#xff0c;解禁市值268.81亿元。 解禁市值超越…
阅读更多...
【第二章 @RequestMapping注解（value，method，params属性），springMVC支持ant风格的路径，支持路径中的占位符】

【第二章 @RequestMapping注解（value，method，params属性），springMVC支持ant风格的路径，支持路径中的占位符】

第二章 RequestMapping注解&#xff08;value&#xff0c;method&#xff0c;params属性&#xff09;&#xff0c;springMVC支持ant风格的路径&#xff0c;支持路径中的占位符 1. RequestMapping注解&#xff1a; &#xff08;1&#xff09; RequestMapping注解的作用就是将请…
阅读更多...
数据结构与算法之桶排序

数据结构与算法之桶排序

目录桶排序概念代码实现时间复杂度桶排序概念 桶排序 &#xff08;Bucket sort&#xff09;或所谓的箱排序&#xff0c;是一个排序算法&#xff0c;工作的原理是将数组分到有限数量的桶里。每个桶再个别排序&#xff08;有可能再使用别的排序算法或是以递归方式继续使用桶排序…
阅读更多...
如何根据实际需求选择合适的三维实景建模方式？

如何根据实际需求选择合适的三维实景建模方式？

随着实景三维中国建设的推进&#xff0c;对三维实景建模的数字化需求大幅增加。由于三维实景建模具有采集速度快、计算精度高等建模优势&#xff0c;引起了各个行业的高度关注。三维实景建模是一种应用数码相机或者激光扫描仪对现有场景进行多角度环视拍摄&#xff0c;然后利用…
阅读更多...
进制转换（详解二进制、八进制、十进制、十六进制的相互转换）

进制转换（详解二进制、八进制、十进制、十六进制的相互转换）

目录二进制运算规则十进制的转换二进制数、八进制数、十六进制数的相互转换&#x1f458;什么是数制 用进位的原则进行计数称为进位计数制&#xff0c;简称数制。进位计数制的特点是表示数值大小的数码与它所处的位置有关&#xff0c;每种数制都包含两个基本的要素&#xff1a;…
阅读更多...
WPF WrapPanel、UniformGrid、DockPanel介绍

WPF WrapPanel、UniformGrid、DockPanel介绍

WPF WrapPanel、UniformGrid、DockPanel介绍 WrapPanel WrapPanel , 具有在有限的容器范围内, 可以自动换行, 或者换列处理。具体则取决于WrapPanel的排列方式 (Orientation)。 Orientation"Horizontal"时各控件从左至右罗列&#xff0c;当面板长度不够时&#xff…
阅读更多...
JMM JVM 垃圾回收

JMM JVM 垃圾回收

目录 一、JMM内存模型 1、定义 2、JMM的三大特性(可见性原子性有序性) 2.1 可见性 2.2 原子性 2.3 有序性 3、JMM中的8种原子操作 二、JVM 1、JVM体系结构 2、JVM参数调优 2.1 三大参数类型 2.2 九个调优参数 三、垃圾回收器 1、4种GC算法(引用计数 /复制拷贝/标…
阅读更多...
深度学习pytorch实战三：VGG16图像分类篇自建数据集图像分类三类

深度学习pytorch实战三：VGG16图像分类篇自建数据集图像分类三类

1.自建数据集与划分训练集与测试集 2.模型相关知识 3.model.py——定义AlexNet网络模型 4.train.py——加载数据集并训练&#xff0c;训练集计算损失值loss&#xff0c;测试集计算accuracy&#xff0c;保存训练好的网络参数 5.predict.py——利用训练好的网络参数后&#xff0c…
阅读更多...
【Taro开发】-文字展开收起组件（十五）

【Taro开发】-文字展开收起组件（十五）

Taro小程序开发 系列文章的所有文章的目录 【Taro开发】-初始化项目&#xff08;一&#xff09; 【Taro开发】-路由传参及页面事件调用&#xff08;二&#xff09; 【Taro开发】-taro-ui&#xff08;三&#xff09; 【Taro开发】-带token网络请求封装&#xff08;四&#x…
阅读更多...
Sonar：Win10搭建SonarQube9.8服务

Sonar：Win10搭建SonarQube9.8服务

需求描述 公司为项目代码配置了Sonar检测&#xff0c;最初只是想调研在VSCode中同步远程检测的方法&#xff08;现在请参考Sonar&#xff1a;VSCode配置SonarLint/SonarLint连接SonarQube&#xff09;&#xff1b;结果并没有找到靠谱的教程。。在度娘的信息海洋胡乱扑腾两天后…
阅读更多...
Docker（七）--Docker数据卷管理及插件

Docker（七）--Docker数据卷管理及插件

文章目录一、Docker 数据卷管理1.bind mount2.docker managed volume3.bind mount与docker managed volume对比二、跨节点存储convoy卷插件一、Docker 数据卷管理 在实际使用过程中&#xff0c;我们需要把容器和数据进行隔离&#xff0c;因为容器在使用过程中可能随时要进行销…
阅读更多...
C++:set和map(模拟实现)

C++:set和map(模拟实现)

目录 关联式容器 键值对 树形结构的关联式容器 set的介绍 set的使用 map的介绍 map的使用 multiset的介绍 multimap的介绍 底层结构 AVL树的概念 AVL树节点的定义 AVL树的旋转 左单旋 右单旋 先右单旋再左单旋 先左单旋再右单旋 模拟实现AVL树 红黑树 红黑树…
阅读更多...
【C++】30h速成C++从入门到精通（stack、queuepriority_queue以及deque介绍）

【C++】30h速成C++从入门到精通（stack、queuepriority_queue以及deque介绍）

stackstack的介绍https://cplusplus.com/reference/stack/stack/?kwstackstack是一种容器适配器&#xff0c;专门在具有后进先出操作的上下文环境中&#xff0c;其删除只能从容器的一端进行元素的插入与提取操作。stack是作为容器适配器被实现的&#xff0c;容器适配器即是对特…
阅读更多...
详解一致性哈希算法

详解一致性哈希算法

在单机系统中&#xff0c;所有的数据都存储在同一个服务器下&#xff0c;当数据量越来越多的时候&#xff0c;超过了单机存储容量的上限&#xff0c;就需要使用分布式存储系统&#xff0c;在分布式存储系统重&#xff0c;数据会被拆分到不同的存储服务下&#xff0c;减少单机服…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023