👘什么是数制

用进位的原则进行计数称为进位计数制，简称数制。进位计数制的特点是表示数值大小的数码与它所处的位置有关，每种数制都包含两个基本的要素：“基数”和“权位”
（1）基数：数码是一组用来表示某种数值的符号，数制所使用的的数码个数就称为“基数”或“基”。一个r进制数具有r个数码：0、1、2、…、r-1，基数为r
（2）权位：数码在不同位置上的权值称为权位，位权是个乘方值，底数为进位计数制的基数，指数由各个数字所在数中的位置决定。
如:十进制3.14=3 * 10 ⁰+1 * 10^-1+4*10 ^-2

👕常见的进制

（1）十进制（D）
十进制是人们最熟悉的一种进位计数制，由0、1、2 …… 9这十个数码组成，基数为10。特点是：逢十进一，借一当十
（2）二进制（B）
二进制是由0和1这两个数码组成，基数为2。特点是：逢二进一，借一当二
（3）八进制（O）
八进制是由0、1、2、3、4、5、6、7这八个数码组成，基数为8。特点是：逢八进一，借一当八
（4）十六进制（H）
十六进制是由0、1、2 …… 9、A、B、C、D、E、F这十六个数码组成，基数为16。特点是：逢十六进一，借一当十六

🎺各进制之间对应关系

十进制	二进制	八进制	十六进制
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

二进制运算规则

（1）算数运算规则
加法规则：0+0=0；0+1=1；1+0=1；1+1=10（向高位进位）
减法规则：1-0=1；1-1=0；0-0=0；10-1=1（向高位借位）
（2）逻辑运算规则
逻辑与运算（AND）：有0为0
逻辑或运算（OR）：有1为1
逻辑非运算（NOT）：0变1,1变0
逻辑异或运算（XOR）：相同为0，不同为1

十进制的转换

（1）二进制、八进制、十六进制数转换为十进制数
方法：“位权展开求和”即按位权展开，然后按照十进制规则进行求和运算，其结果就是转换后对应的十进制数。如：

1️⃣二进制转换为十进制
（1001.01）₂=1 * 2³+0 * 2²+0 * 2¹+1 * 2⁰+0 * 2^-1+1 * 2^-2=9.25

2️⃣八进制转换为十进制
（543.21）₈=5 * 8²+4 * 8¹+3 * 8⁰+2 * 8^-1+1 * 8^-2=355.3125

3️⃣十六进制转换为十进制
（2CF.5）₁₆=2 * 16²+ 12 * 16¹+15 * 16⁰+5 * 16^-1=719.3125

（2）十进制转换为二进制、八进制、十六进制
十进制数的整数部分和小数部分在转换时需要做不同的计算，分别求值后在组合

整数部分采用除r（r为进制数）取余法，即逐次除以r，直至商为0，得出的余数倒排，即为r进制各位的数码。小数部分采用乘r取整法，即逐次乘以r，从每次乘积的整数部分得到r进制数各位的数码，直至小数部分为0，或者满足转换精度的要求为止

1️⃣十进制转换为二进制
如：将十进制226.625转换为二进制数
（1）先对整数226进行转换：

由高位到低位得出：226D=11100010B
（2）对小数部分0.625进行转换

由高位到低位得出：0.625D=0.101B
将整数和小数相加得：226.625D=11100010.101B

2️⃣十进制转换为八进制
如：将十进制226.625转换为八进制数
（1）先对整数226进行转换：

由高位到低位得出：226D=342O
（2）对小数部分0.625进行转换：
0.625*8=5
即：0.625D=0.5O
将整数和小数相加得：226.625D=342.5O

3️⃣十进制转换为十六进制
将十进制226.625转换为十六进制数
（1）先对整数226进行转换：

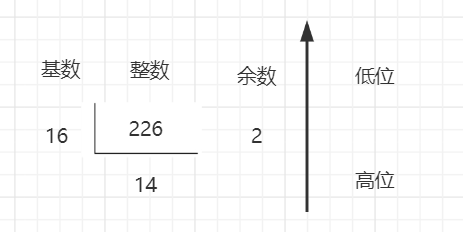
由高位到低位得出：226D=E2H
（2）对小数部分0.625进行转换：
0.625*16=10
即：0.625D=AH
将整数和小数相加得：226.625D=E2.AH

二进制数、八进制数、十六进制数的相互转换

由于二进制、八进制、十六进制之间存在特殊关系；2³=8¹，2⁴=16¹，即一位八进制数相当于3位二进制数，1位十六进制数相当于4位二进制数

1️⃣二进制数转换为八进制

🚩方法：将二进制从小数点开始，对二进制整数部分向左每3位分成一组，不足3位的向高位补0凑成3位；对二进制小数部分向右每3位分成一组，不足3位的向低位补0凑成3位

如：把二进制数11111101.101转换为八进制数

二进制3位分组	011	111	101.	101
转为八进制数	3	7	5.	5

因此， 11111101.101B=375.5O

2️⃣八进制转换为二进制
只需要将每一位八进制数转换为对应的3位二进制数，然后连起来即可
如：把八进制数54.3转换为二进制数
5O=101B
4O=100B
3O=011B
因此，54.3O=101100.011B

3️⃣二进制转换为十六进制

🚩方法：将二进制从小数点开始，对二进制整数部分向左每4位分成一组，不足4位的向高位补0凑成4位；对二进制小数部分向右每4位分成一组，不足4位的向低位补0凑成4位

如：把二进制数11111101.101转换为十六进制数

二进制4位分组	1111	1101.	1010
转为十六进制数	F	D.	A

因此， 11111101.101B=FD.AH

4️⃣十六进制转换为二进制
只需要将每一位十六进制数转换为对应的4位二进制数，然后连起来即可
如：把十六进制数CF.6转换为二进制数
CH=1100B
FH=1111B
6H=0110B

因此， CF.6H=11001111.011B

5️⃣八进制数与十六进制数之间不能直接转换，只能借助二进制数或十进制数作为桥梁然后转换