最近更新的少,主要是因为参加了ACM竞赛
空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。也就是说数据源的空间不能计算在内。
时间一去不复返,也就是说不能够重复利用;但是空间用了之后就能够归还,因此空间可以重复利用,比如下面这个例子:

上面这个的空间复杂度就是O(N),因为我要运行这个算法在这个过程当中,我需要去额外开辟空间,这是跟我的数据源无关的,我额外开辟的空间。

当前函数在调用的时候,为开辟对应的函数栈帧,如果函数里面又会调用函数,那么当前函数的函数栈帧并不会被销毁,上面这个的空间复杂度也是O(N)

那么重头戏来了,这个的空间复杂度是多少?首先的话必须要了解到底函数的调用顺序是怎么样的?就看我的这张图:
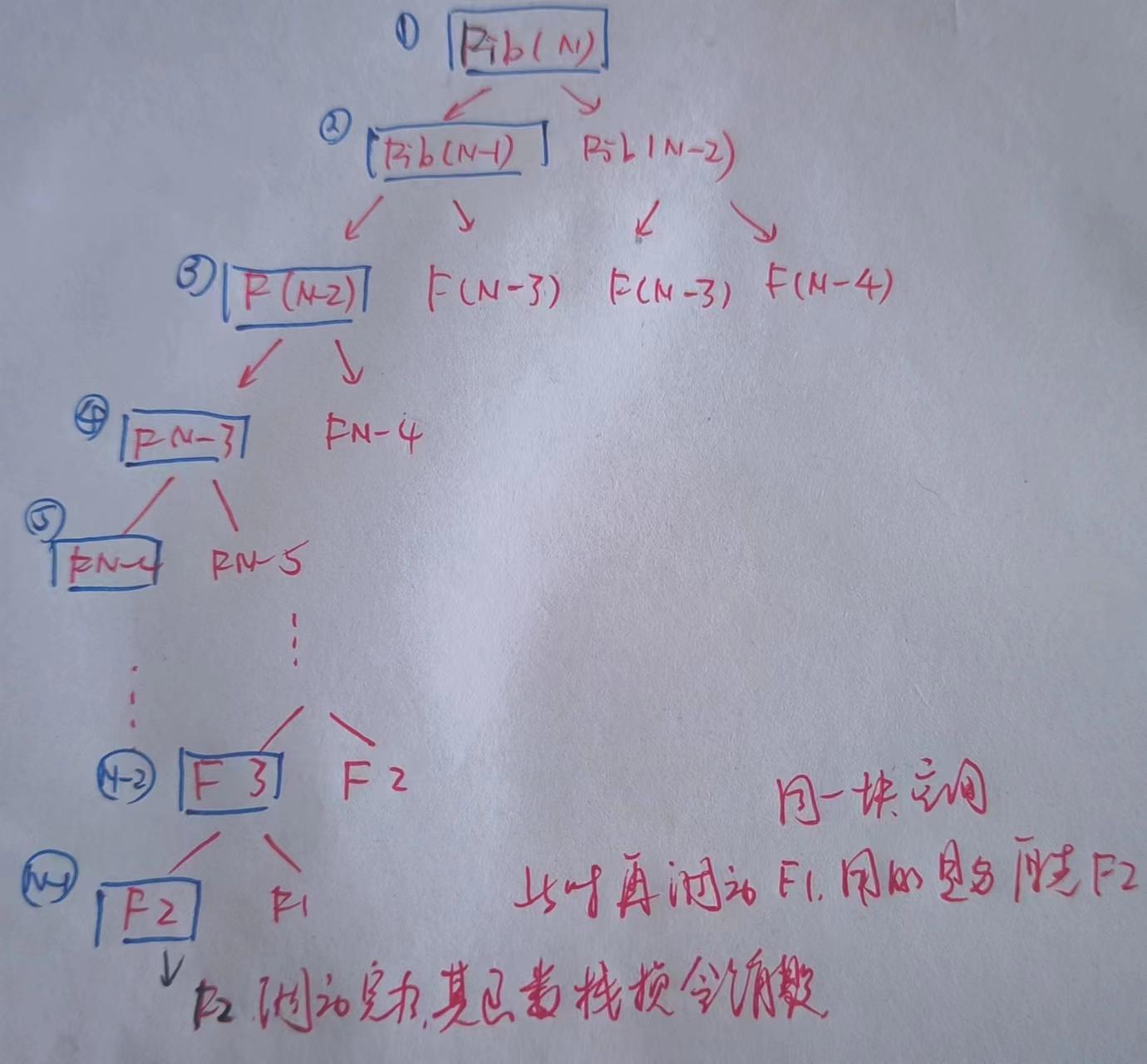
这种函数执行的顺序有点类似于深度优先搜索,到底了之后那个函数执行结束之后就会销毁函数栈帧,接下来再去调用函数,对于总的空间来说已经不会再增加,因此空间复杂度就是O(N)。
虽然说空间复杂度统计的是变量的个数,如果说函数里面并没有创建变量,那么我们认为在这个函数栈帧里面的空间大小为一个常数,也就是O(1)。
对于数组而言,有几个元素就表示所谓的变量个数。
线性表
数据结构的作用:在内存当中存储与管理数据。
线性表是n个具有相同特性的数据元素的有限序列,线性表是一种常用的数据结构。比较常见的线性表有:顺序表,链表,栈,队列,字符串.......。我们说线性表在逻辑上是线性结构,也就是说好比一条连续的直线。但是在物理结构上并不一定是连续的。在物理上存储时,通常以数组和链式结构的形式存储
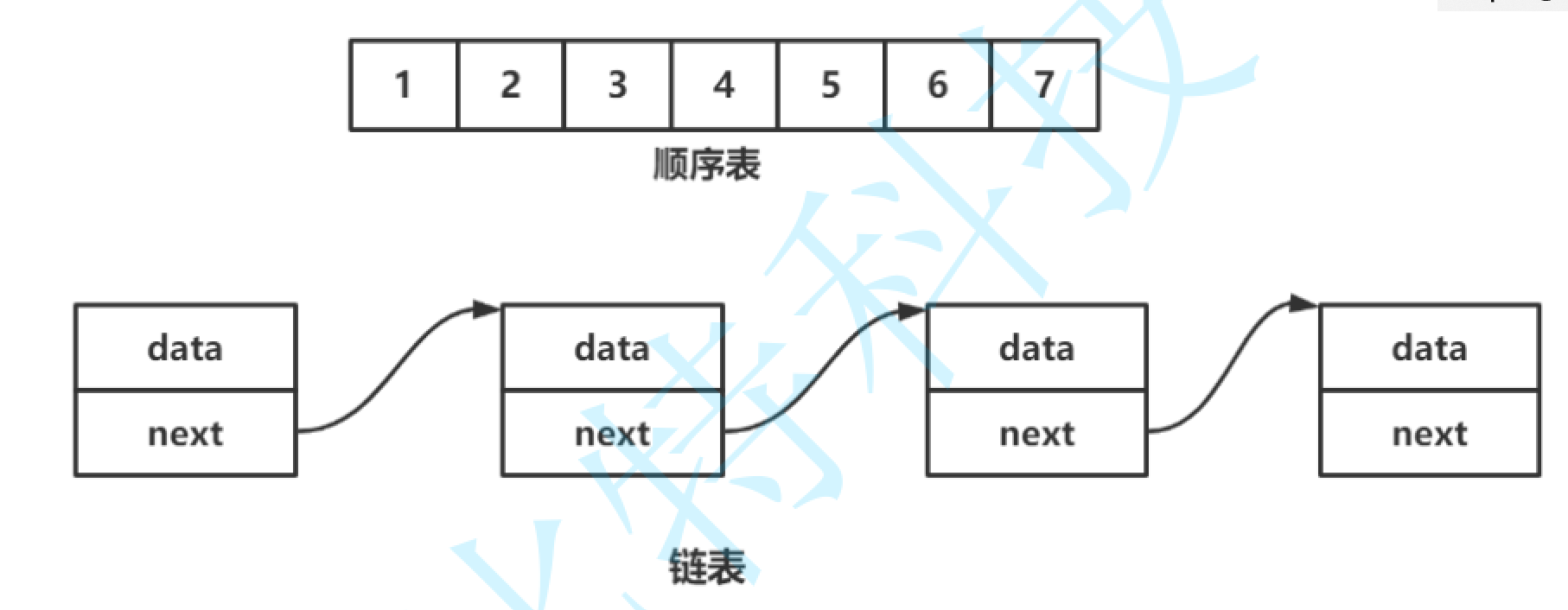
顺序表(SeqList)
顺序表就是写一个结构体,然后通过这个结构对数组进行管理,存储数据就是用数组存储

1.创建一个顺序表
//创建一个结构体
typedef int SLDataType;
typedef struct SeqList
{
SLDataType* p;
size_t size;
size_t capacity;
}SeqList;2.顺序表的初始化
#define INIT_CAPACITY 5
void SeqListInit(SeqList* ps)
{
ps->p = (SeqList*)malloc(sizeof(SLDataType) * INIT_CAPACITY);
if (ps->p = NULL)
{
perror("SeqListInit::Malloc:");
return;
}
ps->size = 0;
ps->capacity = INIT_CAPACITY;
}3.顺序表使用结束后的销毁
void SeqListDestroy(SeqList* ps)
{
free(ps->p);
ps->p = NULL;
ps->capacity = 0;
ps->size = 0;
}4.打印顺序表
void SeqlistPrint(SeqList* ps)
{
for (int i = 0; i < ps->size; i++)
{
printf("%d ", *(ps->p + i));
}
printf("\n");
}5.顺序表的尾插
void SeqListPushBack(SeqList* ps, SLDataType x)
{
if (ps->size == ps->capacity)
{
SLDataType* pp = (SLDataType*)realloc(ps->p, sizeof(SLDataType) * ps->capacity * 2);
if (pp == NULL)
{
perror("SeqListPushBack::Realloc");
return;
}
ps->p = pp;
}
*(ps->p + ps->size) = x;
ps->capacity *= 2;
ps->size++;
}6.顺序表的尾删
void SeqListPopBack(SeqList* ps)
{
assert(ps->size > 0);
ps->size--;
}未完,待续........