A.愤怒的牛儿
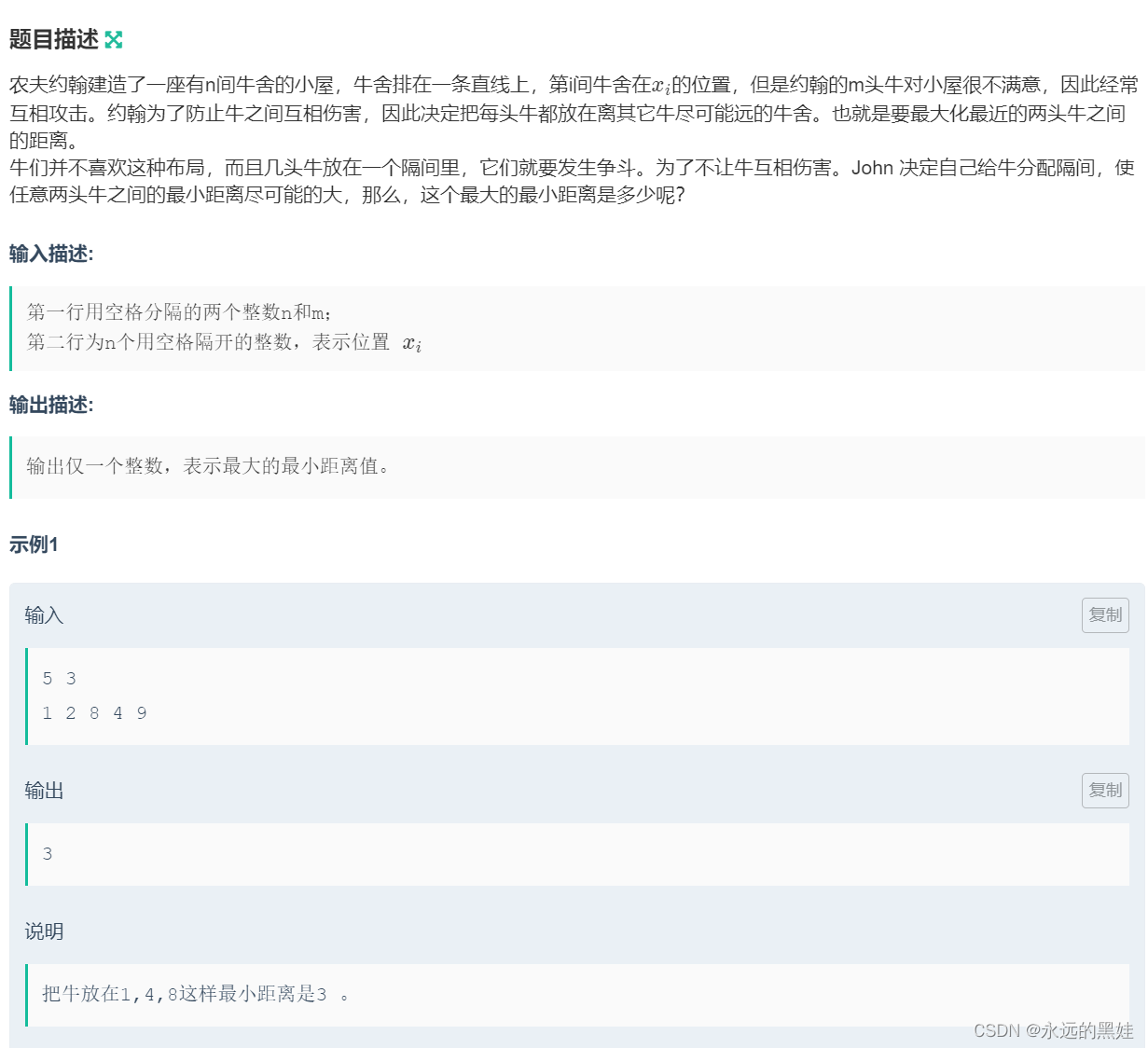
思路:找出最长距离,与最小距离,用二分法判断,如果当前距离满足放牛要求,就把距离区间l=mid+1;如果距离不合适就说明当前距离太大了,把区间变小r=mid-1;最后直到l<r不满足时退出,输出ans;ans=mid,在遍历的时候保存。
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e9+10;
int num[100010];
int n,m;
int judge(int dis)
{
int dum=1;
int xi=num[1];
for(int i=2;i<=n;i++)
{
if(num[i]-xi>=dis)
{
dum++;
xi=num[i];
}
if(dum==m)break;
}
return dum==m;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>num[i];
sort(num+1,num+1+n);
int l=num[1];
int r=num[n]-num[1]+1;
int k;
while(l<r)
{
int mid=(l+r)>>1;
if(judge(mid)){k=mid;l=mid+1;}
else r=mid;
}
cout<<k;
}B.Best Cow Fences
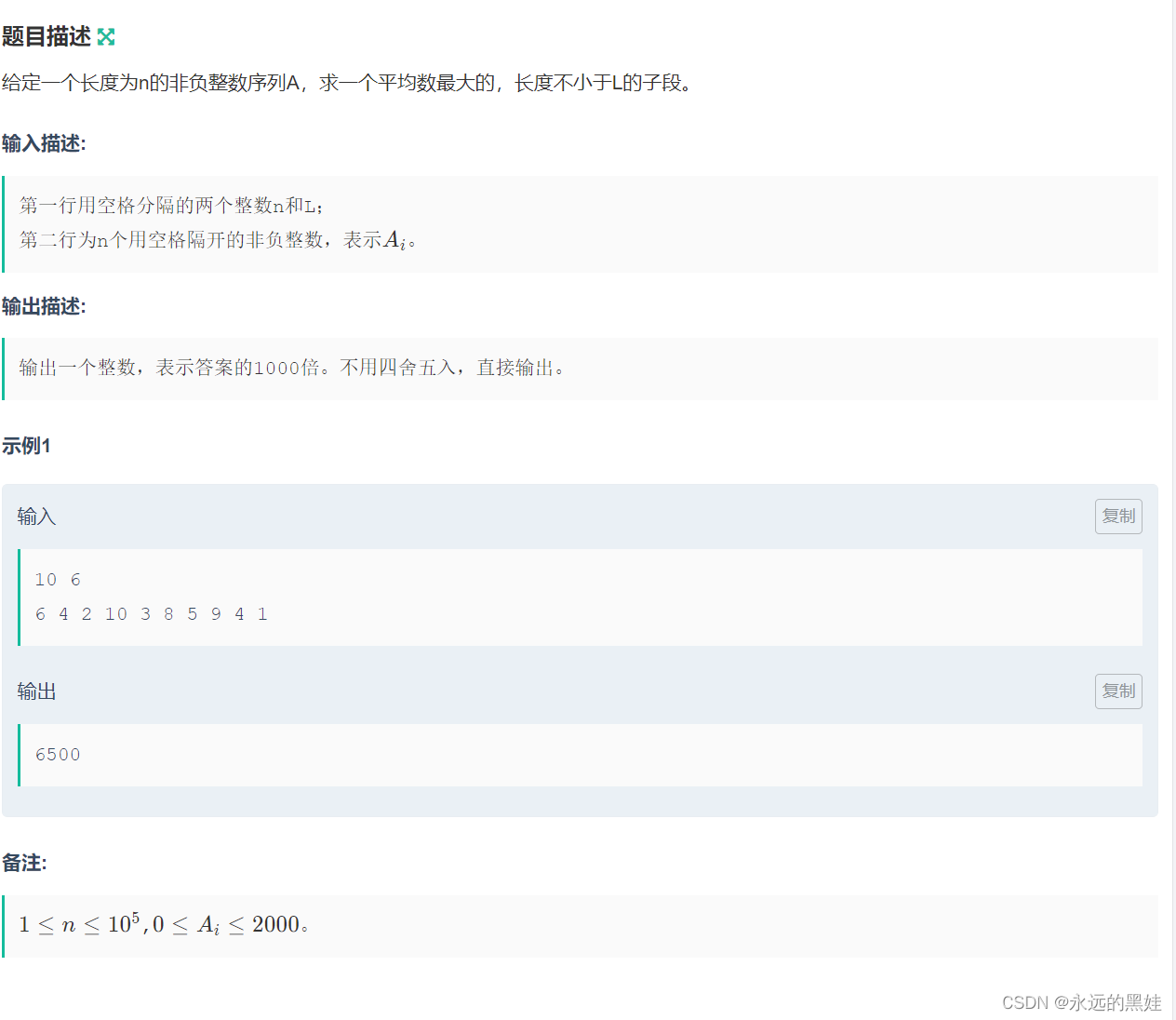
思路:看到了平均值就知道应该要用前缀和了,我们要输出平均数最大的,当然就要考虑用二分了。我们依旧用二分法,每一次如果该平均值满足条件,我们就把区间l=mid;(这里为什么不l=mid+1;因为这样会跳过答案)。如何判断呢就是我们用前缀和,前缀和在开始的时候要把传过来的平均值直接减去,看看是否小于0即可。取最大平均值过程中是这样的,把前面最小的保存下来。然后用后面的减去那个最小值看看是否大于0即可。最好输出即可l或r。
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int n,m;
double num1[maxn];
double num2[maxn];
bool judge(double ave)
{
for(int i=1;i<=n;i++)num2[i]=num2[i-1]+num1[i]-ave;//每次都减去平均值
double mins=maxn;//筛出最小前缀值
for(int i=m;i<=n;i++)//从最短距离开始
{
mins=min(num2[i-m],mins);
if(num2[i]-mins>0)return true;
}
return false;
}
int main()
{
cin>>n>>m;
double l=0,r=0;
for(int i=1;i<=n;i++)
{
cin>>num1[i];
r=max(num1[i],r);
}
while(r-l>1e-6)
{
double mid=(l+r)/2;
if(judge(mid))l=mid;
else r=mid;
}
printf("%d\n",(int)(1000*r));
}C.曲线
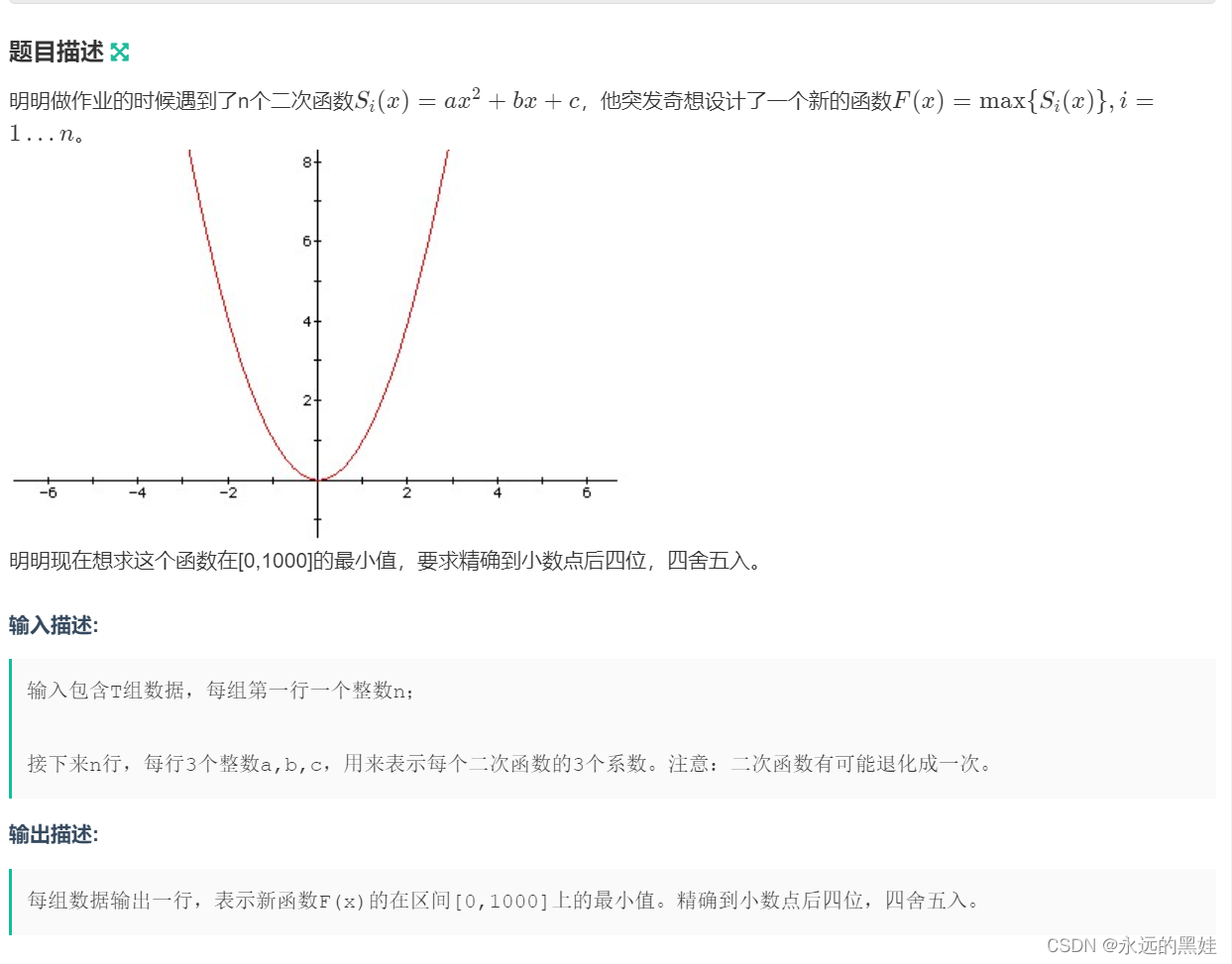

思路:单峰函数用三分法。具体方法如下。
#include<bits/stdc++.h>
using namespace std;
int num;
int num1;
double a[20005],b[20005],c[20005];
double judge(double x)//返回值
{
double mas=INT_MIN;
for(int i=1;i<=num1;i++)
{
mas=max(mas,a[i]*x*x+b[i]*x+c[i]);//选出最大的那个值
}
return mas;
}
void solves()
{
cin>>num1;
for(int i=1;i<=num1;i++)
{
cin>>a[i]>>b[i]>>c[i];
}
double left=0,right=1000;
while(right>left+1e-4)//精度
{
double midleft=left+(right-left)/3;//三分左区间
double midright=right-(right-left)/3;//三分右区间
if(judge(midleft)>=judge(midright))//如果左高的话说明左离得远
{
left=midleft;//移动左区间
}
else right=midright;//否则移动右区间
}
printf("%.4f\n",judge(left));
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>num;
while(num--)
{
solves();
}
}D.数列分段
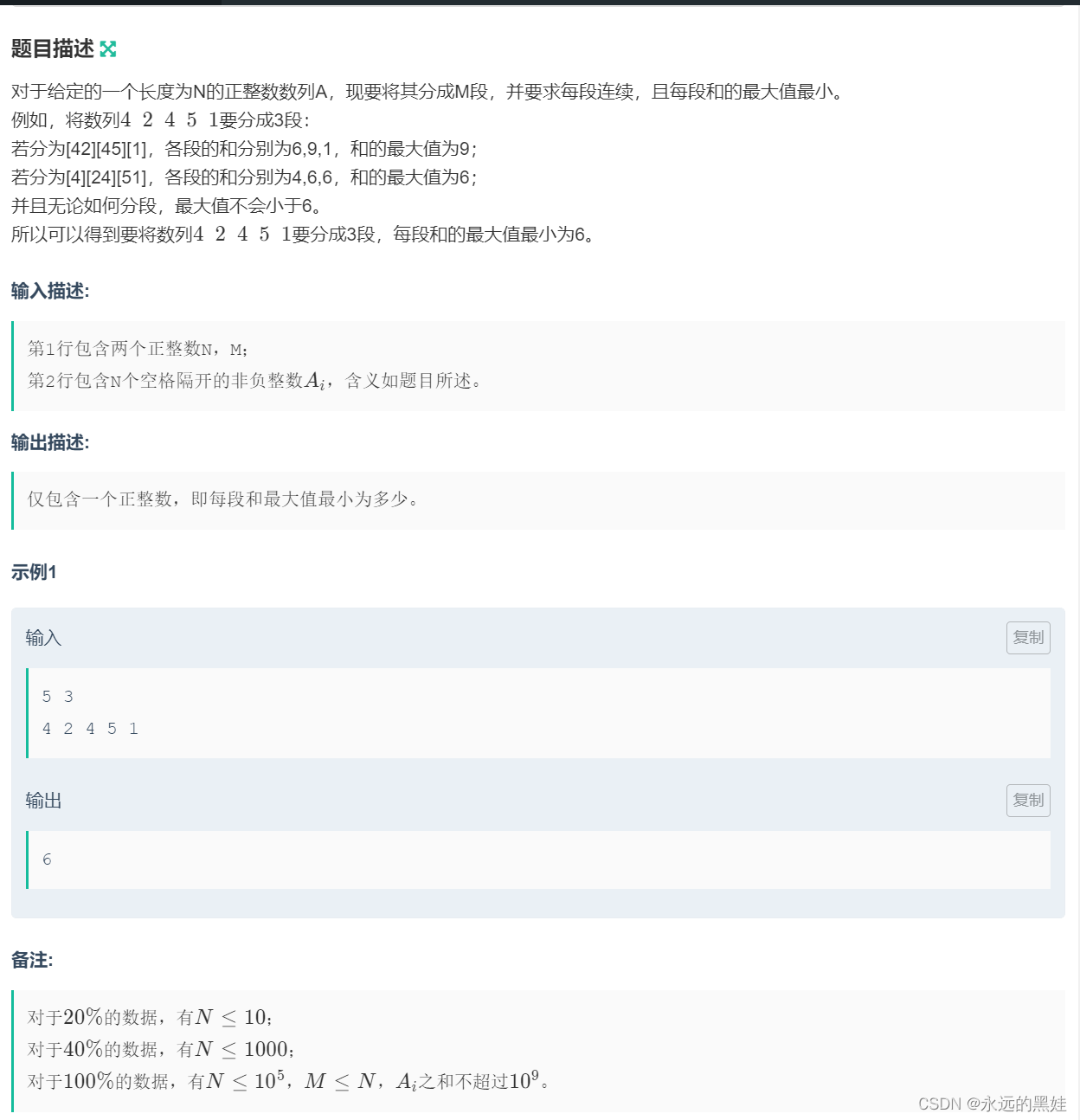
思路:依旧是二分思路,取全和做R,取1做L,移动区间即可。对于满足条件就把区间r=mid,不满足条件就l=mid+1;最后输出r。判断函数写法具体是,看看是否能在段数不大于m的情况,满足条件。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+10;
int n,m;
ll num[maxn];
int check(int x)
{
ll sum=0;
int cnt=1;
for(int i=1;i<=n;i++)
{
if(num[i]>x)return 0;
sum+=num[i];
if(sum>x)
{
sum=num[i];
cnt++;
}
}
return m>=cnt;
}
int main()
{
cin>>n>>m;
int l=1,r=0;
for(int i=1;i<=n;i++)
{
cin>>num[i];
r+=num[i];
}
while(l<r)
{
int mid=l+r>>1;
if(check(mid))r=mid;
else l=mid+1;
}
cout<<r<<endl;
}E.扩散
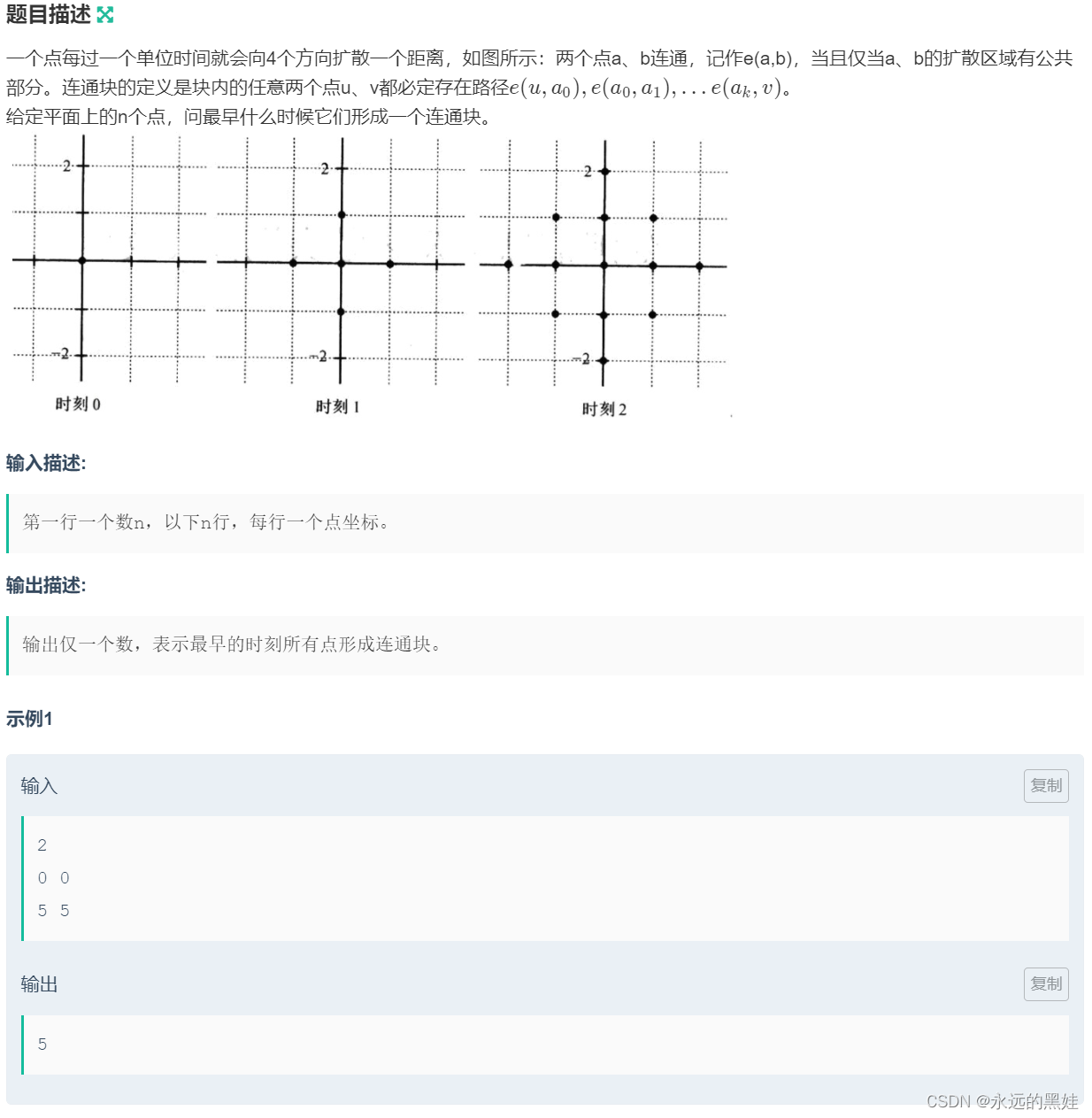
思路:依旧是二分,但需要并查集的协助,我们设置最大时间R=1e9+10,最小时间L=0.我们开始二分算法,如果当前时间满足条件,就把时间区间R=mid;否则L=mid+1.最后输出R。判断函数具体思路是我们设置二重循环,每一次访问两个点看看能不能在当前时间内是否能扩散相交。具体条件是x,y坐标差值与两倍时间的大小关系。如果小于或等于则可以扩散到,反之则不可以。如果扩散到的话就,放到并查集中,如果没有就不用放。之后看看每个点是否只有一个祖先即可。
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+10;
int x[maxn],y[maxn];
int father[maxn];
int n;
int find(int x)
{
if(father[x]==x)return x;
else return find(father[x]);
}
bool check(int mid)
{
int sum=0;
for(int i=1;i<=n;i++)father[i]=i;
for(int i=1;i<=n;i++)
{
for(int i1=i+1;i1<=n;i1++)
{
if(abs(x[i]-x[i1])+abs(y[i]-y[i1])<=2*mid)
{
if(find(i)!=find(i1))
{
father[find(i)]=find(i1);
}
}
}
}
for(int i=1;i<=n;i++)
{
if(father[i]==i)sum++;
if(sum==2)return false;
}
return true;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>x[i]>>y[i];
}
int l=0,r=1e9+10;
int ans;
while(l<r)
{
int mid=r+l>>1;
if(check(mid))
{
r=mid;
}
else l=mid+1;
}
cout<<r;
}H.灯泡
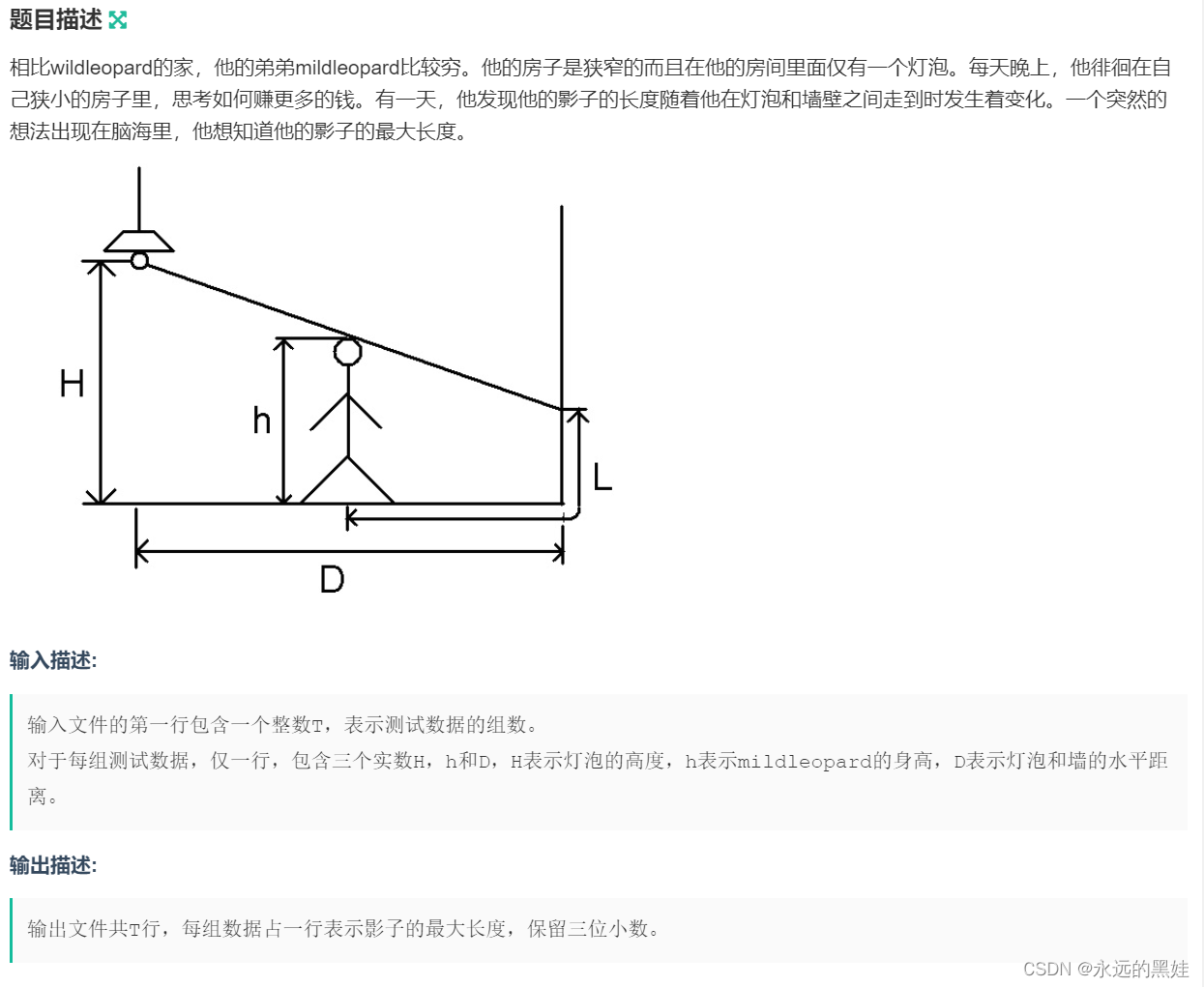

思路:根据计算所得影子长度就两种情况
(1)当影子不会射到墙上时,影子长度为
(2)当影子射到了墙上时,影子长度为
看函数我们将x定义为等到人的距离。看函数是一个单峰函数。所以用三分法去做。具体如下
#include<bits/stdc++.h>
using namespace std;
double H,h,D;
double check(double x)
{
if(D-x>h*x/(H-h))//影子长度小于人到墙的距离
{
return h*x/(H-h);//返回第一种情况
}
else
{
return D-x+h-(H-h)*(D-x)/x;//反之影子在墙上,返回第二种情况。
}
}
void solve()
{
cin>>H>>h>>D;
double l=0;
double r=D;
while(r-l>1e-6)
{
double midl=l+(r-l)/3;
double midr=r-(r-l)/3;
if(check(midl)>=check(midr))//单峰函数移动法
{
r=midr;
}
else l=midl;
}
printf("%.3f\n",check(r));
}
int main()
{
int num;cin>>num;
while(num--)
{
solve();
}
}
G.传送带
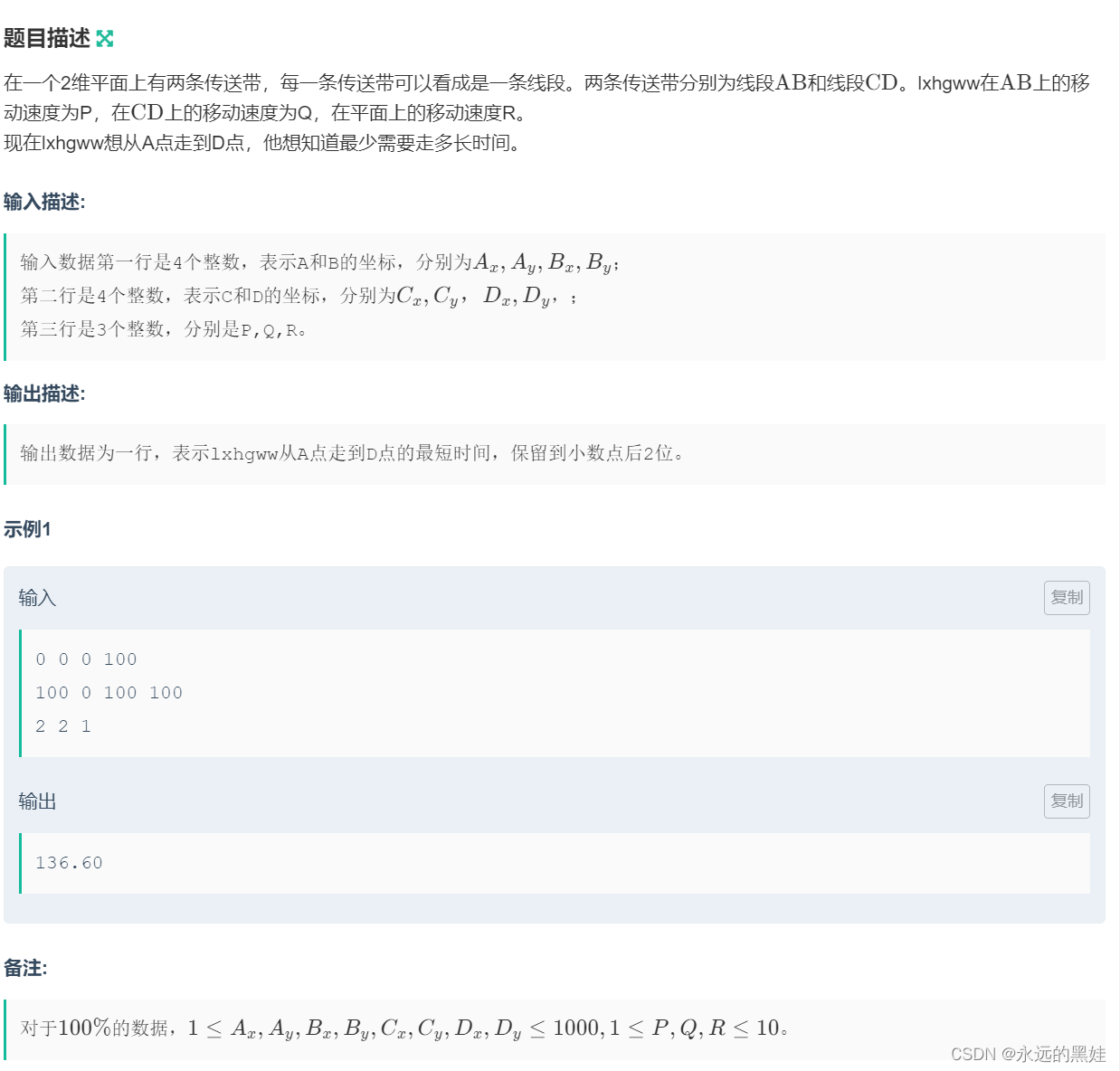
思路:这道题有点难度,想了好久,学习了好久才会的。共有三段路程,一段在AB上,一段在CD上,还有一段在路上。很简单看一下,那个最少时间满足单谷函数。所以我们用三分,但未知量有两个所以我们用三分套三分。具体如下
#include<bits/stdc++.h>
using namespace std;
double Ax,Ay,Bx,By,Cx,Cy,Dx,Dy,p,q,r,ans;
double check(double x,double y)
{
double P1x=Ax+(Bx-Ax)*x,P1y=Ay+(By-Ay)*x,P2x=Cx+(Dx-Cx)*y,P2y=Cy+(Dy-Cy)*y;
return sqrt((P1x-Ax)*(P1x-Ax)+(P1y-Ay)*(P1y-Ay))/p+sqrt((Dx-P2x)*(Dx-P2x)+(Dy-P2y)*(Dy-P2y))/q+sqrt((P2x-P1x)*(P2x-P1x)+(P2y-P1y)*(P2y-P1y))/r;
}
double find2(double x,double l,double r)//在CD上三分
{
double res=0.0;//返回的时间数
while(r-l>=1e-6)//精度
{
double midl=l+(r-l)/3;
double midr=r-(r-l)/3;
double res1=check(x,midl);//按在AB中的比例,和CD中的比例返回时间
double res2=check(x,midr);
if(res1<res2)//缩短区间,保留答案。
{
r=midr;
res=res1;
}
else l=midl,res=res2;
}
return res;
}
void find1(double l,double r)
{
while(r-l>=1e-6)
{
double midl=l+(r-l)/3;//在AB上三分
double midr=r-(r-l)/3;
double res1=find2(midl,0,1);//用三分出来的比例在CD上看返回来的值分布情况
double res2=find2(midr,0,1);
if(res1<res2)
{
r=midr;
ans=res1;
}
else
{
l=midl;
ans=res2;
}
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>Ax>>Ay>>Bx>>By>>Cx>>Cy>>Dx>>Dy>>p>>q>>r;//输入
find1(0,1);//这里的0,1是在AB上的比例。
printf("%.2f",ans);
}