一、强制类型转换

强制类型转换是把变量从一种类型转换为另一种数据类型。例如，如果您想存储一个 long 类型的值到一个简单的整型中，您需要把 long 类型强制转换为 int 类型。您可以使用强制类型转换运算符来把值显式地从一种类型转换为另一种类型，如下所示：

(type_name) expression

使用强制类型转换运算符把一个整数变量除以另一个整数变量，得到一个浮点数

#include <stdio.h>
 
int main()
{
   int sum = 17, count = 5;
   double mean;
 
   mean = (double) sum / count;
   printf("Value of mean : %f\n", mean );
 
}

Value of mean : 3.400000

这里要注意的是强制类型转换运算符的优先级大于除法，因此 sum 的值首先被转换为 double 型，然后除以 count，得到一个类型为 double 的值。

类型转换可以是隐式的，由编译器自动执行，也可以是显式的，通过使用强制类型转换运算符来指定。在编程时，有需要类型转换的时候都用上强制类型转换运算符，是一种良好的编程习惯

二、整数提升

整数提升是指把小于 int 或 unsigned int 的整数类型转换为 int 或 unsigned int 的过程。请看下面的实例，在 int 中添加一个字符：

#include <stdio.h>
 
int main()
{
   int  i = 17;
   char c = 'c'; /* ascii 值是 99 */
   int sum;
 
   sum = i + c;
   printf("Value of sum : %d\n", sum );
 
}

Value of sum : 116

在这里，sum 的值为 116，因为编译器进行了整数提升，在执行实际加法运算时，把 ‘c’ 的值转换为对应的 ascii 值

三、常用的算术转换

常用的算术转换是隐式地把值强制转换为相同的类型。编译器首先执行整数提升，如果操作数类型不同，则它们会被转换为下列层次中出现的最高层次的类型：
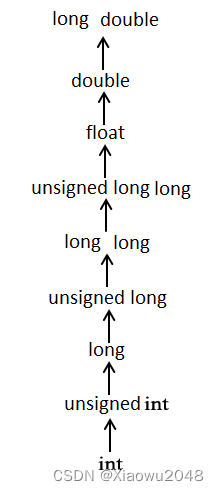
在这里插入图片描述
常用的算术转换不适用于赋值运算符、逻辑运算符 && 和 ||。让我们看看下面的实例来理解这个概念

#include <stdio.h>
 
int main()
{
   int  i = 17;
   char c = 'c'; /* ascii 值是 99 */
   float sum;
 
   sum = i + c;
   printf("Value of sum : %f\n", sum );
 
}