浮点数的表示

表示

为什么会有浮点数？位数有限的情况下，既扩大了数的范围，也保持了数的精度。

浮点数的意思是小数点是浮动的，阶码的值决定了小数点是怎么"浮动"的。

浮点数公式：

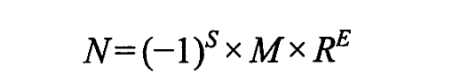
浮点数组成

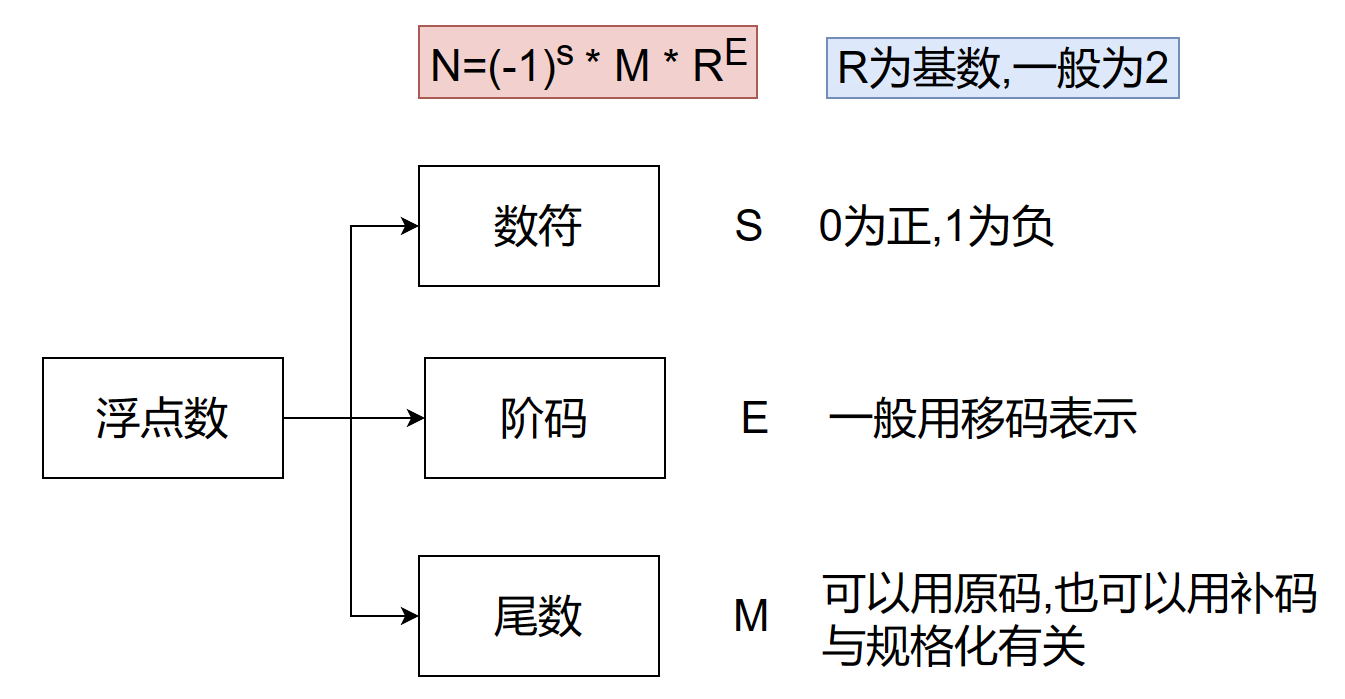
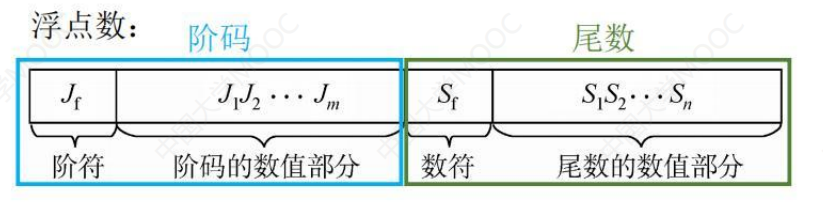
阶码由阶符和数位组成，阶符就是阶码的符号。0表示正，1表示负

数符就是尾数的符号。0表示正，1表示负

从这可以看出，这个定义太松散了，比如没有规定阶符几位，尾数数符几位等等，所以如果没有一个统一的标准去规定浮点数那浮点数在计算机中的存储就会多种多样，所以后面就有了IEEE754标准。

溢出

溢出的概念

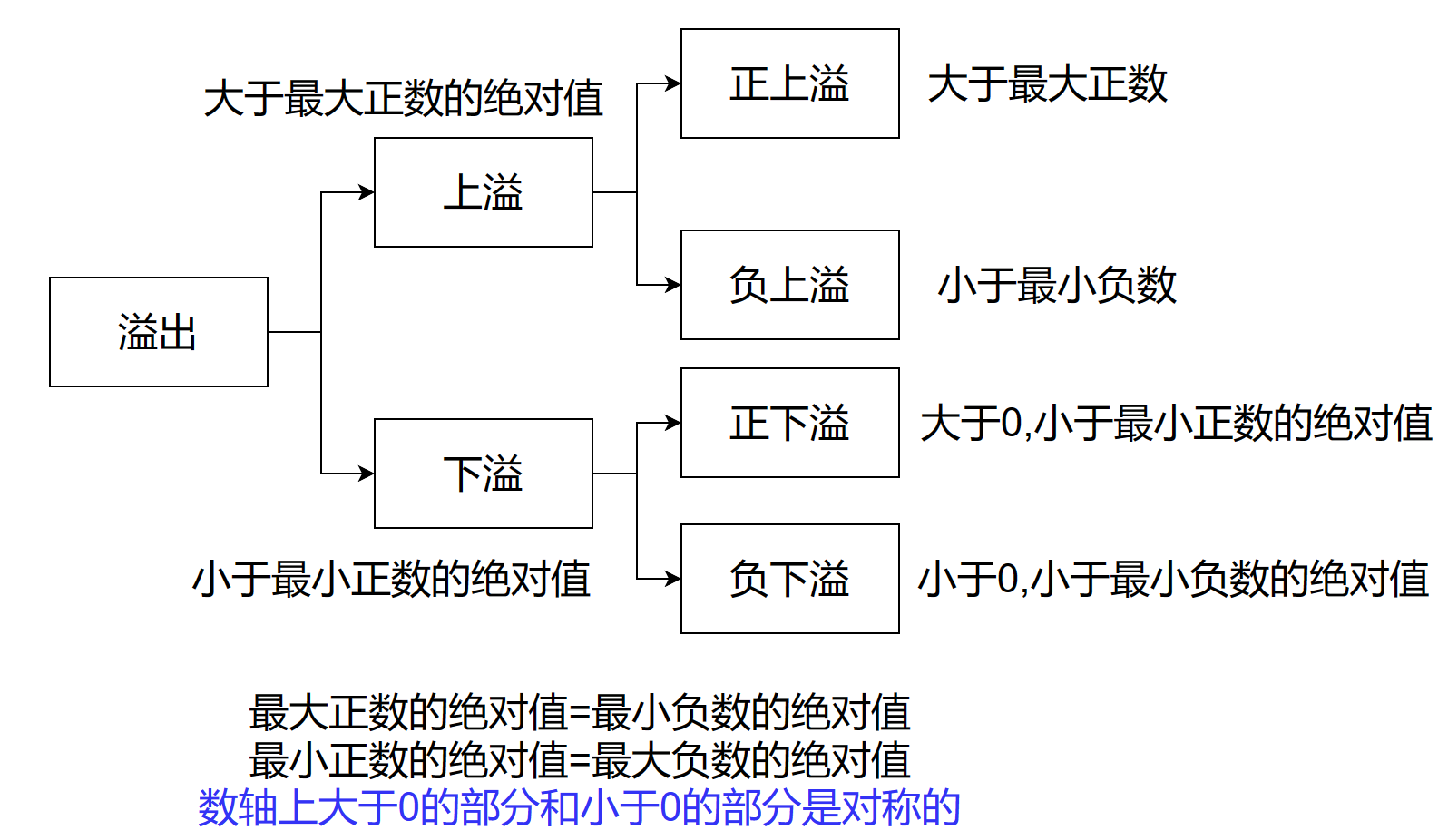
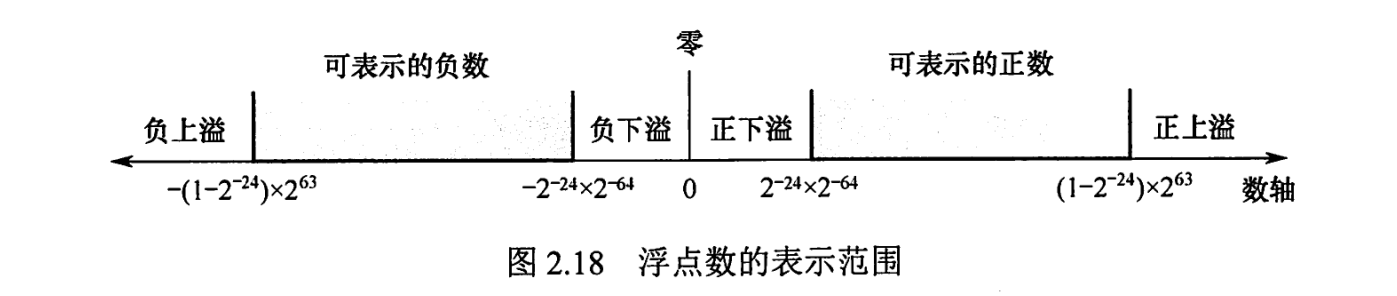
数轴上溢出的图示

溢出时计算机的处理：上溢时直接中断处理溢出，下溢时直接当做机器数0

规格化

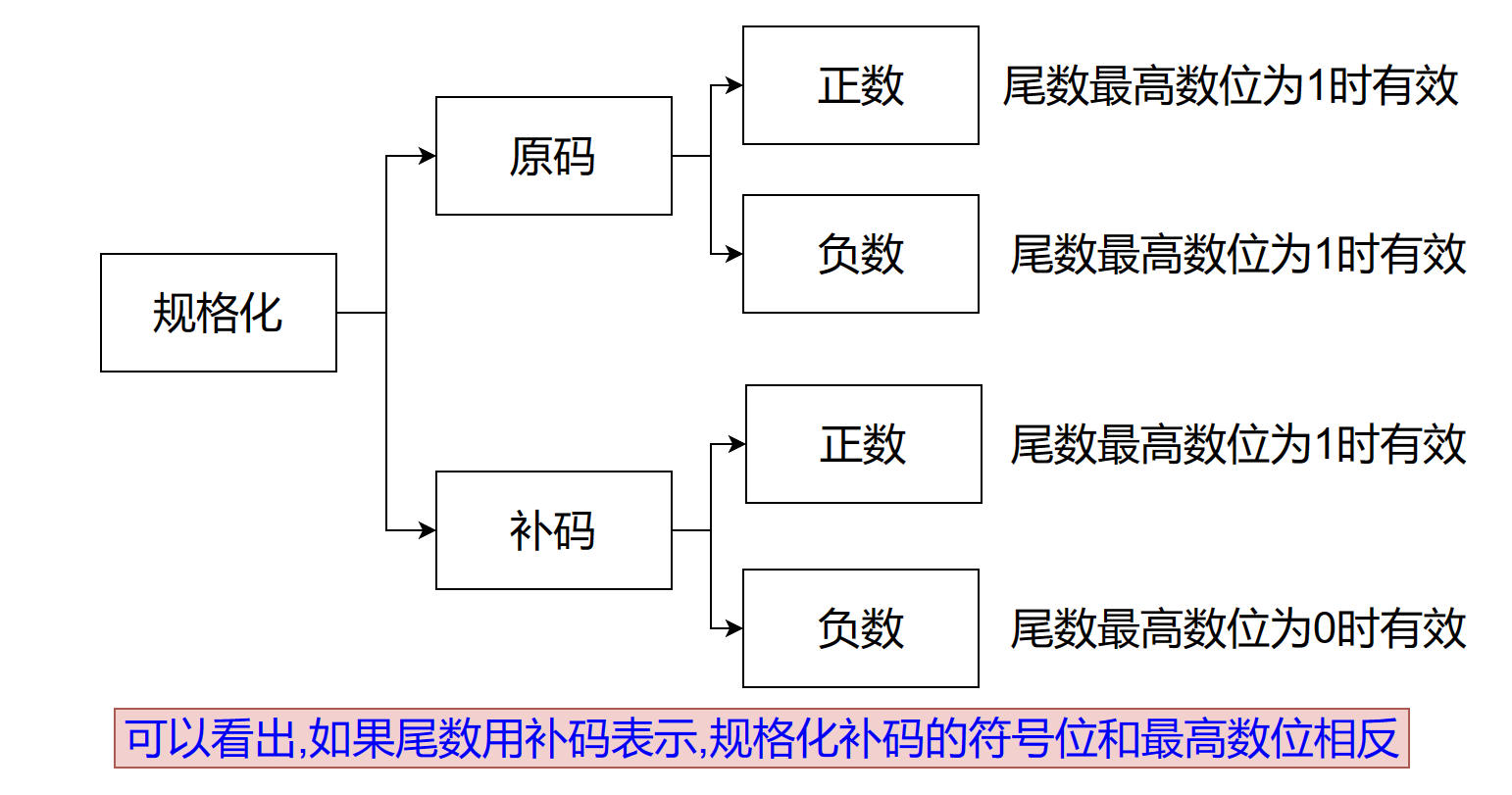
规格化：通过尾数移动和阶码变化来实现尾数最高数位为有效位。

举个例子，0.000011* 10⁰D,其中尾数000011里的0000都不是有效数位，如果尾数直接存就是6位，所以可以移动尾数变成0.11*10^-4,现在的尾数就是11了，我们存进去就只需要两位，在机器字长有限的情况下，规格化可以使得有效位数更多，进而使得精度更高

左规可以简单理解为左移，左移一位，阶码减一

右规可以简单理解为右移，右移一位，阶码加一。可能损失精度

注意移动的是数不是小数点

规格化还与基数有关，以二进制为例，当基数为2时，则最高数位为有效数位。基数为4时，则最高的两位数位为有效数位。基数为8时，则最高的三位数位为有效数位。我的理解是基数为4时，两个二进制位才表示一个数，保证这个数是有效的即可。一般情况下默认基数为2，除非特别声明。

我们说的有效数位，可以理解为有意义，但是有效数位≠不为0，得考虑尾数是原码还是补码。原码时，有效数位就是1，所以让最高数位为1就是规格化。但如果是负数的补码时，0才是有效数位（补码按位取反+1后，最高数位的0会变成1）。

IEEE754

IEEE754是一种浮点数标准，C语言里用的浮点数标准就是IEEE754.。

格式

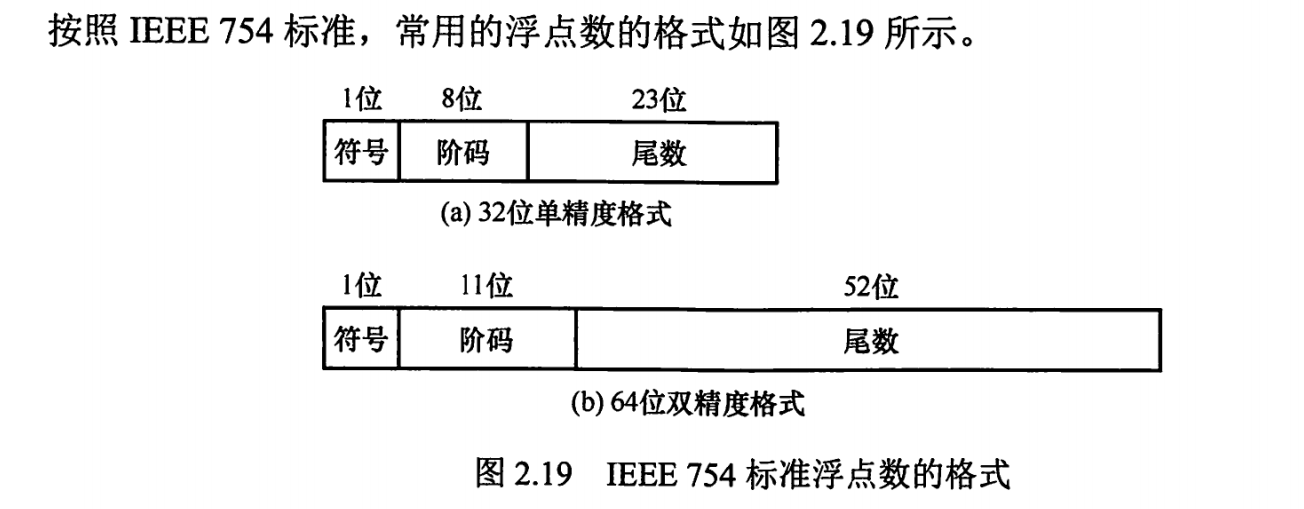
可以看出主要分为32位精度和64位精度的，其中32位记住1,8,23，64位记住1,11,52。

以32位为例，符号位为0表示正，为1表示负。阶码一般由移码表示，偏置量是127（2^8-1-1)。尾数是23位，一般是原码表示（算的时候不用再取反了），尾数实际精度是24位，由于规格化的原因最高数位必为1，所以可直接隐藏掉1，所以看上去23位精度其实是24位。

单精度浮点数 - 维基百科)

浮点数真值的计算公式

短浮点数指的就是32位的，长浮点数就是64位。其中E-127是因为阶码偏移值是127（2^8-1-1），64位的偏移值是2^11-1-1=1023,所以E-1023就能得到阶码的真值。

范围

32位浮点数移码的偏移量是127，一般移码的偏移量会定为128，所以这里会有一些变化。

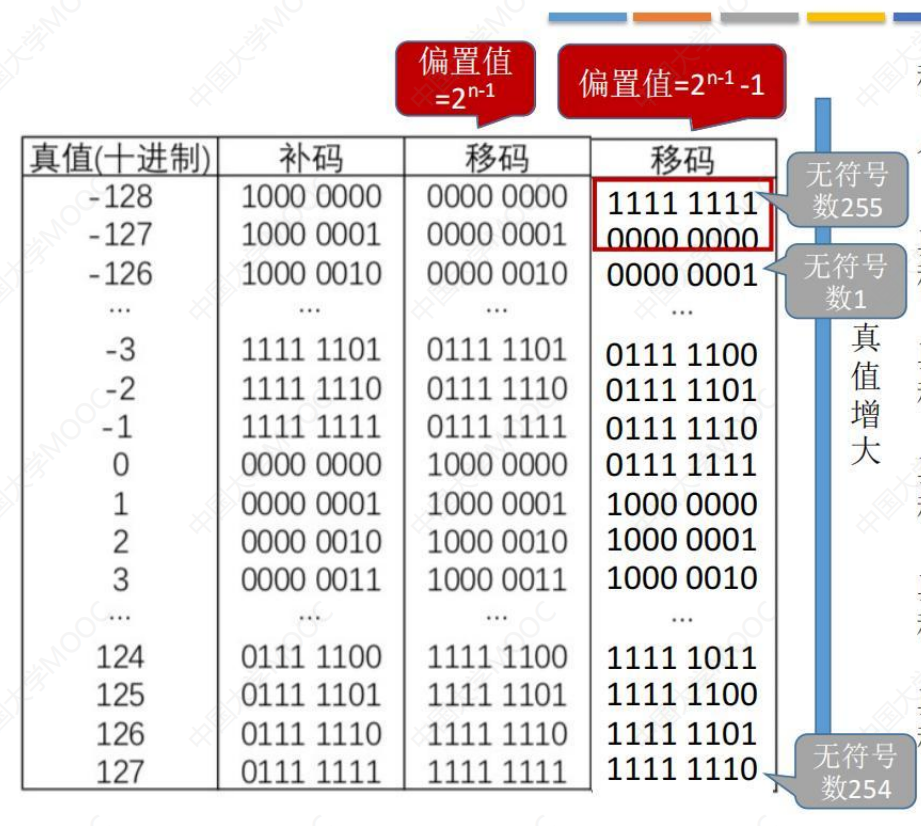
从图中可以看出移码全0和全1代表的真值是-128和-127,这两个数有特殊含义。

可以稍作了解，一般不考。

不考虑这些特殊情况，我们可以探讨下浮点数的范围。

以浮点数大于0时的范围为例

浮点数小于0的部分和大于0是对称的,所以知道大于0的，改变一下符号就能知道小于0的

最大值：

0 11111110 11111111111111111111111 （符号为正，阶码最大254，尾数全为1）

再套一下公式(-1)⁰*1.11111111111111111111111 *2^254-127=(1+(1-2^-23)) *2¹²⁷=2¹²⁷ *(2+2^-23)

最小值：

0 00000001 00000000000000000000000

(-1)⁰*1.00000000000000000000000 *2^1-127=1 *2^-126=2^-126

所以负的浮点数的范围就是[-2¹²⁷ *(2+2^-23),-2^-126 ]。

注意这里的范围都是规格化的，非规格化的小数可以更小。

浮点数的加减

建议去看王道视频

chatgpt:

1. 对于参与运算的两个浮点数，首先需要将它们的指数部分进行比较，使它们的指数部分相同。这可以通过将指数较小的数的尾数部分向右移动，直到它们的指数相同。
2. 然后，将它们的尾数部分进行加减运算。在进行加减运算之前，需要考虑它们的符号。如果两个数的符号相同，则进行加法运算；如果符号不同，则进行减法运算。
3. 完成加减运算后，需要对结果进行规格化处理。规格化处理是将结果转换为科学计数法的形式，使得尾数部分的最高位为1，从而达到最大的精度。
4. 最后，对规格化后的结果进行舍入处理，得到最终的结果。舍入处理是将尾数部分按照指定的舍入规则进行四舍五入等操作，使得结果满足给定的精度要求。

总之，浮点数的加减法需要将指数部分进行比较，尾数部分进行加减运算，规格化处理和舍入处理等步骤，以得到最终的结果。

加减的步骤：

1. 写出二进制（一般是补码）

2. 对阶，将阶数小的扩大到与阶数大的相等，再向右移动尾数。（如果是阶码大的变成阶码小的，那尾数要向左移，小数点前面的位数就不好确定导致电路不好设计）

3. 尾数相减

   尾数采用双符号位溢出的同时，尾数可以通过第四步的规格化使其不再溢出。

4. 规格化，注意如果是负数补码规格化的话最高数位得是0、

5. 舍入

6. 判断溢出，一般都是判断阶码是否溢出。

例子：

规格化移位的同时别忘了阶码也要改变。

最后的结果一般还需要转为原码表示。

浮点数的乘除

今年考纲对乘除不做要求，了解即可。

浮点数的乘除法运算_浮点数除法_xiaotai1234的博客-CSDN博客

其实之前有想过这么一个问题，既然float范围大还能保持一定的精度，那为什么还要int,long之类的整形变量，以int和float举例，float尾数可表示的实际精度是24位，而int是31位，所以从这个角度看int类型虽然范围比float小，但是精度比int高。

刷题小结

• 基数大表示的范围大，精度低。

• 负数补码尾数规格化最高位注意是0不是1。

• IEEE754的尾数采用的是原码表示。

• 两个正的规格化浮点数如果阶数不同直接比较阶数就行

• 基数不同，规格化要注意的位数也不同

• 对阶和右规时可能需要舍入（都发生了右移）

• 算出结果后还有最后一步判断溢出，比如算出的结果阶码的双符号为01，这就是溢出了。

• double+float也要对阶，两个浮点数一对阶发生右移可能导致精度丢失，如果double的阶远大于float的阶，那float对阶右移后的尾数可能全变为0.

• 浮点数的加减法：对阶不会引起阶码上溢或者下溢（因为对阶是让小的阶对齐到大的阶，大的阶本身没溢出，那对阶就不可能导致溢出），右规和尾数舍入使得阶码变大可能导致上溢，左规使得阶码减小可能导致下溢，尾数溢出不代表结果溢出，因为尾数溢出可以通过规格化纠正