文章目录
- 一、priority_queue 的介绍和使用
- 1、priority_queue 的介绍
- 2、priority_queue 的使用
- 3、priority_queue 相关 OJ 题
- 二、仿函数
- 1、什么是仿函数
- 2、仿函数的作用
- 三、priority_queue 的模拟实现
一、priority_queue 的介绍和使用
1、priority_queue 的介绍
priority_queue (优先级队列) 是一种容器适配器,它与 queue 共用一个头文件,其底层结构是一个堆,并且默认情况下是一个大根堆,所以它的第一个元素总是它所包含的元素中最大的,并且为了不破坏堆结构,它也不支持迭代器: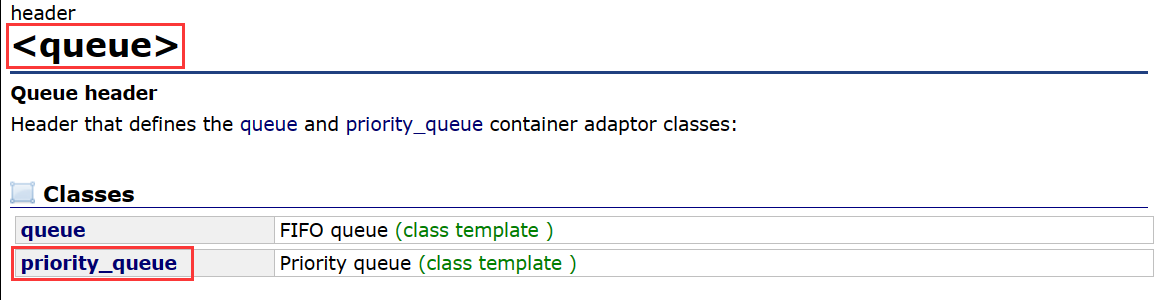
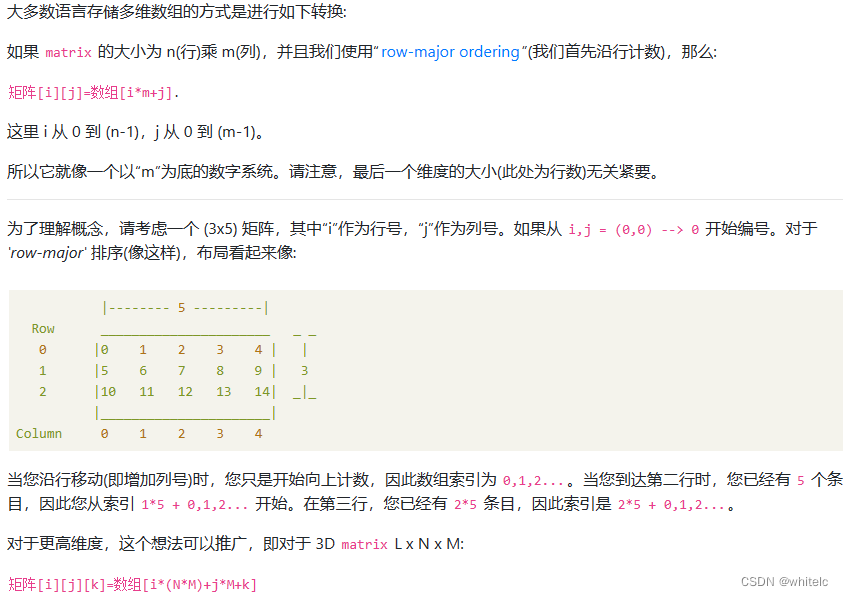
同时,由于堆需要进行下标计算,所以 priority_queue 使用 vector 作为它的默认适配容器 (支持随机访问):
但是,priority_queue 比 queue 和 stack 多了一个模板参数 – 仿函数;关于仿函数的具体细节,我们将在后文介绍。
class Compare = less<typename Container::value_type>
2、priority_queue 的使用
优先级队列默认使用 vector 作为其底层存储数据的容器,在 vector 上又使用了堆算法将 vector 中元素构造成堆的结构,因此 priority_queue 就是堆,所有需要用到堆的位置,都可以考虑使用 priority_queue。(注意:默认情况下priority_queue是大堆)
priority_queue 的使用文档
| -函数声明 | 接口说明- |
|---|---|
| priority_queue() | 构造一个空的优先级队列 |
| priority_queue(first, last) | 迭代器区间构造优先级队列 |
| empty( ) | 检测优先级队列是否为空 |
| top( ) | 返回优先级队列中最大(最小元素),即堆顶元素 |
| push(x) | 在优先级队列中插入元素x |
| pop() | 删除优先级队列中最大(最小)元素,即堆顶元素 |
| size() | 返回优先级队列中的元素个数 |
注意事项:
priority_queue 默认使用的仿函数是 less,所以默认建成的堆是大堆;如果我们想要建小堆,则需要指定仿函数为 greater,该仿函数包含在头文件 functional 中,并且由于仿函数是第三个缺省模板参数,所以如果要传递它必须先传递第二个模板参数即适配容器。

void test_priority_queue() {
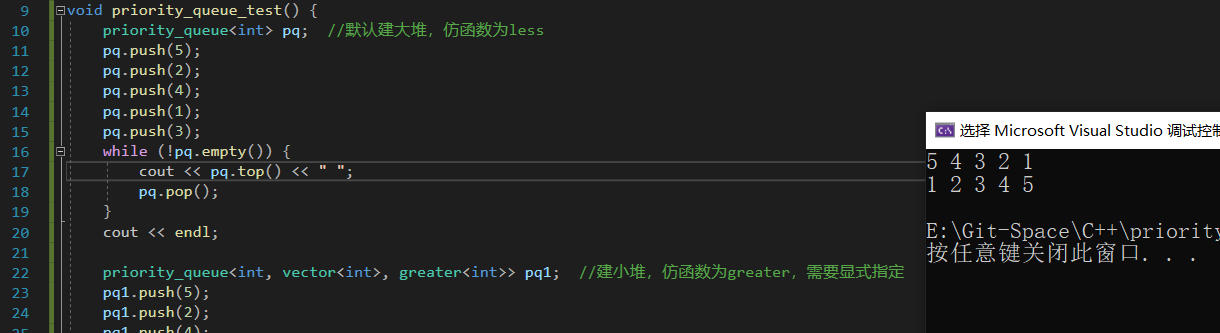
priority_queue<int> pq; //默认建大堆,仿函数为less
pq.push(5);
pq.push(2);
pq.push(4);
pq.push(1);
pq.push(3);
while (!pq.empty()) {
cout << pq.top() << " ";
pq.pop();
}
cout << endl;
priority_queue<int, vector<int>, greater<int>> pq1; //建小堆,仿函数为greater,需要显式指定
pq1.push(5);
pq1.push(2);
pq1.push(4);
pq1.push(1);
pq1.push(3);
while (!pq1.empty()) {
cout << pq1.top() << " ";
pq1.pop();
}
cout << endl;
}
3、priority_queue 相关 OJ 题
215. 数组中的第K个最大元素 - 力扣(LeetCode)
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例
输入: [3,2,1,5,6,4], k = 2 输出: 5 输入: [3,2,3,1,2,4,5,5,6], k = 4 输出: 4
思路1
思路1非常简单,直接对 nums 数组使用 sort 进行排序,然后返回 nums[nums.size() - k] 即可,但是排序的时间复杂度为 O(N*logN),太高。
思路2
思路2就是建N个数的大堆,然后 pop k-1 次,此时堆顶元素就是第 K 大的数,向下调整建堆时间复杂度为 O(N),pop 再向下调整的时间复杂度为 K*logN,所以总的时间复杂度为 O(N + K*logN);此方法可行,但是当 N 很大,K 很小时,空间复杂度过高。
思路3
建 K 个数的小堆,剩余 N- K 个数依次与堆顶元素进行比较,如果大于堆顶元素就将堆顶元素 pop 掉,然后将其 push 进堆中,最后堆顶元素就是第 K 大的数;建堆的时间复杂度为 O(K),push 再向上调整的时间复杂度为 O((N-k)*logK),所以总的时间复杂度为 O(K + (N-k) * logK);此方法在 N 很大,K 很小的情况下依然适用,因为堆的大小固定为 K。
代码实现
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
priority_queue<int, vector<int>, greater<int>> pq; //建小堆
for(int i = 0; i < k; i++) { //建K个数的小堆
pq.push(nums[i]);
}
for(int i = k; i < nums.size(); i++) { //剩余n-k个数与堆顶比较,大于就删除堆顶元素入堆
if(nums[i] > pq.top()) {
pq.pop();
pq.push(nums[i]);
}
}
return pq.top(); //堆顶元素为第K大的数
}
};
二、仿函数
1、什么是仿函数
仿函数也叫函数对象,仿函数是一个类,但是该类必须重载函数调用运算符 (),即 operator()(参数);由于这样的类的对象可以像函数一样去使用,所以我们将其称为仿函数/函数对象,如下:
namespace thj {
template<class T>
struct less {
bool operator()(const T& x, const T& y) const {
return x < y;
}
};
template<class T>
struct greater {
bool operator()(const T& x, const T& y) {
return x > y;
}
};
}
void functor_test() {
thj::less<int> lessFunc;
cout << lessFunc(1, 2) << endl; //lessFunc.operator(1,2)
thj::greater<int> greaterFunc;
cout << greaterFunc(1, 2) << endl; //greaterFunc.operator(1,2)
}

可以看到,因为 less 类和 greater 类重载了 () 操作符,所以类对象可以像函数一样去使用,因此它们被称为仿函数。
2、仿函数的作用
我们以最简单的冒泡排序为例来说明仿函数的作用,我们知道,排序分为排升序和排降序,那么在没有仿函数的时候,即C语言阶段,我们是如何来解决这个问题的呢 – 答案是函数指针;
将排序函数的最后一个参数定义为函数指针,然后通过用户给排序函数传递不同的比较函数来决定升序还是降序:
template<class T>
bool cmpUp(const T& e1, const T& e2) { //排升序
return e1 > e2;
}
template<class T>
bool cmpDown(const T& e1, const T& e2) { //排降序
return e1 < e2;
}
// 冒泡排序
template<class T>
void BubbleSort(T* a, int n, bool (*cmp)(const T&, const T&))
{
T i = 0;
T j = 0;
for (i = 0; i < n - 1; i++)
{
int exchange = 0;
for (j = 0; j < n - i - 1; j++)
{
if (cmp(a[j], a[j + 1])) //函数调用
{
std::swap(a[j], a[j + 1]);
exchange = 1;
}
}
if (exchange == 0) break;
}
}
void bubbleSort_test() {
int a[] = { 1, 3, 2, 2, 4, 8, 5, 1, 9 };
BubbleSort(a, sizeof(a) / sizeof(int), cmpUp);
for (auto e : a) {
cout << e << " ";
}
cout << endl;
int b[] = { 1, 3, 2, 2, 4, 8, 5, 1, 9 };
BubbleSort(b, sizeof(b) / sizeof(int), cmpDown);
for (auto e : b) {
cout << e << " ";
}
cout << endl;
}
在 C++ 中,我们不再使用函数指针解决升序降序的问题,转而使用更加方便的仿函数。(注:关于仿函数的更多细节以及仿函数和函数指针各自的优缺我们将在以后慢慢学习,现在仅仅是浅浅入门一下仿函数)
// 冒泡排序
template<class T, class Compare>
void BubbleSort(T* a, int n, Compare cmp) //使用仿函数
{
T i = 0;
T j = 0;
for (i = 0; i < n - 1; i++)
{
int exchange = 0;
for (j = 0; j < n - i - 1; j++)
{
if (cmp(a[j], a[j + 1])) //函数调用 cmp.operator()(a[j], a[j+1])
{
std::swap(a[j], a[j + 1]);
exchange = 1;
}
}
if (exchange == 0) break;
}
}
//复用前面的 less 和 greater 类
void bubbleSort_test1() {
int a[] = { 1, 3, 2, 2, 4, 8, 5, 1, 9 };
BubbleSort(a, sizeof(a) / sizeof(int), thj::less<int>()); //排降序,匿名对象
for (auto e : a) {
cout << e << " ";
}
cout << endl;
int b[] = { 1, 3, 2, 2, 4, 8, 5, 1, 9 };
BubbleSort(b, sizeof(b) / sizeof(int), thj::greater<int>()); //排升序
for (auto e : b) {
cout << e << " ";
}
cout << endl;
}
三、priority_queue 的模拟实现
其实 priority_queue 的模拟实现我们已经做过了 – priority_queue 的底层是堆,而关于堆的C语言实现包括堆的应用 (堆排序与TopK问题) 我们在数据结构初阶都已经做过了,这里只是用类和对象,再加上容器适配器和仿函数将其封装起来而已,所以下面我就直接给出实现代码而不进行细节分析了,如果有疑问的同学可以回头看看我之前的博客。
【数据结构】二叉树 – 堆
【数据结构】堆的应用 – 堆排序和TopK问题
priority_queue.h:
#pragma once
namespace thj {
//仿函数
template<class T>
struct less {
bool operator()(const T& x, const T& y) const {
return x < y;
}
};
template<class T>
struct greater {
bool operator()(const T& x, const T& y) {
return x > y;
}
};
//priority_queue
template<class T, class Container = vector<T>, class Compare = less<T>> //默认建大堆,传less
class priority_queue {
public:
priority_queue() {} //默认构造
template<class InputIterator>
priority_queue(InputIterator first, InputIterator last) //迭代器区间构造
: _con(first, last)
{
//向下调整建堆 O(N) 从最后一个非叶子节点开始
for (int i = (_con.size() - 1 - 1) / 2; i >= 0; i--) {
adjustDown(i);
}
}
bool empty() const { //判空
return _con.empty();
}
size_t size() const { //元素个数
return _con.size();
}
const T& top() const { //取堆顶数据
return _con[0];
}
void push(const T& x) { //插入数据
_con.push_back(x);
adjustUp(_con.size() - 1); //从最后一个节点开始向上调整
}
void pop() { //删除堆顶数据
std::swap(_con[0], _con[_con.size() - 1]); //为了不破坏堆结构,先将第一个元素和最后一个交换
_con.pop_back();
adjustDown(0); //从堆顶向下调整
}
void adjustDown(size_t parent) { //堆的向下调整
Compare cmp; //仿函数
size_t child = parent * 2 + 1;
while (child < _con.size()) { //特别注意边界问题
if (child + 1 < _con.size() && cmp(_con[child], _con[child + 1])) { //仿函数
child = child + 1; //如果是less,则建大堆,找大孩子,结果为真,右孩子大
}
if (cmp(_con[parent], _con[child])) {
std::swap(_con[parent], _con[child]);
//迭代
parent = child;
child = parent * 2 + 1;
}
else break; //满足堆结构,跳出循环
}
}
void adjustUp(size_t child) { //堆的向上调整
Compare cmp;
size_t parent = (child - 1) / 2;
while (child > 0) { //一直向上调整到根节点
if (cmp(_con[parent], _con[child])) {
std::swap(_con[parent], _con[child]);
child = parent;
parent = (child - 1) / 2;
}
else break;
}
}
private:
Container _con;
};
}
test.cpp:
#include "priority_queue.h"
#include <iostream>
#include <functional>
#include <vector>
#include <algorithm>
using namespace std;
void my_priority_queue_test() {
thj::priority_queue<int> pq; //默认建大堆,仿函数为less
pq.push(5);
pq.push(2);
pq.push(4);
pq.push(1);
pq.push(3);
while (!pq.empty()) {
cout << pq.top() << " ";
pq.pop();
}
cout << endl;
thj::priority_queue<int, vector<int>, thj::greater<int>> pq1; //建小堆,仿函数为greater,需要显式指定
pq1.push(5);
pq1.push(2);
pq1.push(4);
pq1.push(1);
pq1.push(3);
while (!pq1.empty()) {
cout << pq1.top() << " ";
pq1.pop();
}
cout << endl;
std::vector<int> v;
v.push_back(1);
v.push_back(8);
v.push_back(2);
v.push_back(3);
v.push_back(6);
thj::priority_queue<int> pq2(v.begin(), v.end()); //迭代器区间构造
while (!pq2.empty()) {
cout << pq2.top() << " ";
pq2.pop();
}
cout << endl;
}