计算机组成原理

计算机系统概述

问题一、冯诺依曼机基本思想

1. 存储程序：程序和数据都存储在同一个内存中，计算机可以根据指令集执行存储在内存中的程序。这使得程序具有高度灵活性和可重用性。
2. 指令流水线：将指令分成若干阶段，每个阶段执行不同的操作，可以在同一时刻处理多条指令。这样可以提高计算机的执行效率。
3. 二进制数系统：指令和数据都以二进制的形式存储在设备中，计算机能够通过不同指令周期读取的二进制数据加以区分。
4. 存储器层次结构：计算机系统包含多层存储器，不同层次的存储器提供不同的容量、速度和成本。这种存储器层次结构可以满足不同应用程序对存储器的不同需求。
5. 组成：计算机由处理器、控制器、存储器、输入设备与输出设备组成，其中计算机是以运算器为中心。

问题二、计算机指标

• 字长（机器字长）：通常指CPU内部能够用于整数运算的数据通路的宽度，反映了计算机处理信息的能力。通常一台机器的字长与通用寄存器的位数相同。
  • 指令字长：一条指令中包含的二进制位数，指令字长是存储字长的整数倍。
  • 存储字长：一个存储单元内的二进制代码的长度，与MDR的位数相同。
• 吞吐量：单位时间内，某一个系统内处理的请求数量
• 流水线吞吐率：单位时间内流水线完成任务数量
• **流水线加速比：**同一批任务，不使用流水线与使用流水线的时间之比。
• CPI：执行一条指令需要的时钟周期数。
• MIPS：每秒执行的指令数量，单位：百万
• MFLOPS/GFPLPS/TFLOPS ：每秒执行的浮点运算次数，单位：百万/十亿/万亿

---

数据的表示

问题一、原码，补码，负数补码的转换

原码 <——> 补码：从右到左第一个1，这个1左侧的**所有“数值位”**取反。

补码<——> 负数补码：从左到右第一个1，这个1左侧的全部位取反。

---

问题二、大端存储方式与小端存储方式

数据存储格式：左高右低

大端存储方式：高地址存放在低有效字节（符合人类阅读习惯）

小端存储方式：低地址存放在高有效字节

---

指令系统

问题一、基址寻址与变址寻址的区别

**基址寻址（Base Addressing）**是一种寻址方式，它通过将一个基础地址和一个偏移地址相加得到访问的地址。基址寄存器存储基础地址，偏移地址可以是一个常量或者是一个寄存器的值，基址寻址是面向操作系统的。基址寻址可以让程序员将程序中的逻辑地址转换为物理地址，从而实现访问内存的功能，有利于多道程序设计。

**变址寻址（Indexed Addressing）**是一种寻址方式，它通过将一个基础地址和一个偏移地址相加得到访问的地址，这个偏移地址是由一个寄存器存储的值加上一个常量得到的，变址寻址方式是面向用户的。这种寻址方式适用于随机访问数组，编制循环程序。

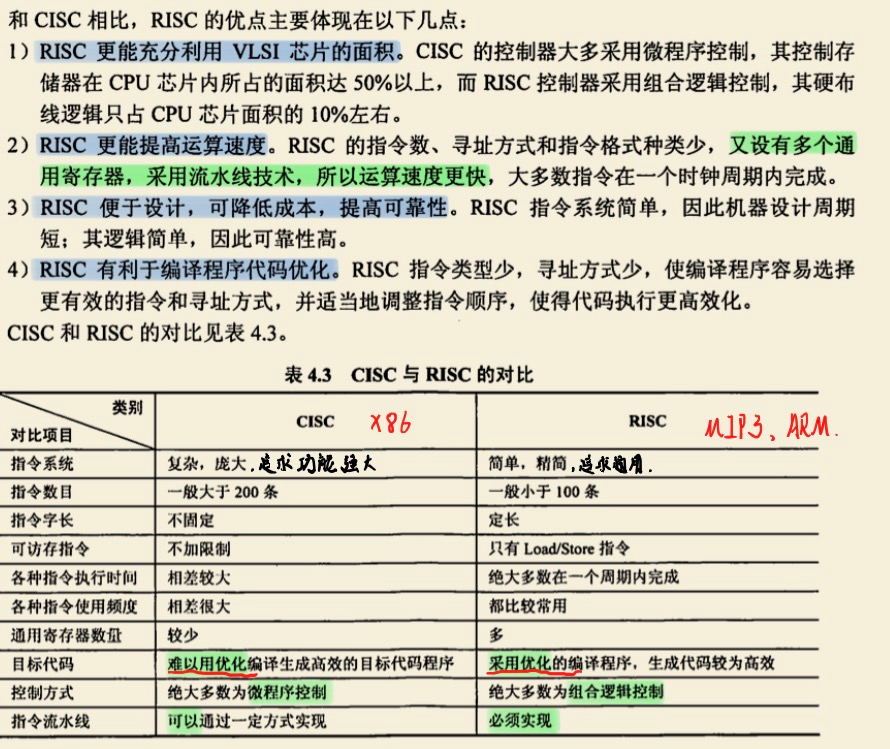
问题二、RISC 与 CISC 的比较

---

中央处理器

问题一、指令周期的构成

1. 取指周期：读取PC的值送入MAR中，读取内存中的指令放入MDR后放回IR(指令寄存器)。
2. 间址周期：根据操作数的寻址方式获取操作数的物理地址。
3. 执行周期：取出操作数，执行指令。
4. 中断周期：保护程序断点。

问题二、简述一下什么是指令流水线

流水线（pipeline）是一种提高计算机CPU效率的技术，它通过将指令执行过程拆分成多个阶段，让每个阶段可以独立执行，并且在同一时刻可以有多个指令在不同阶段执行，从而提高指令执行的吞吐量和效率。

流水线的冒险

数据冒险（数据冲突）

• 概念：数据相关指在一个程序中，存在必须等前一条指令执行完才能执行后一条指令的情况，则这两条指令即为数据相关。
• 解决办法：
  • 数据旁路技术（转发机制）：不等前一条指令把计算结果写回寄存器组，下一条指令不再读寄存器组，而是直接把前一条指令的计算结果作为自己的输入数据开始计算过程
  • 暂停流水线：把遇到数据相关的指令及其后续指令都暂停一至几个时钟周期，直到数据相关问题消失后再继续执行。可分为硬件阻塞（stall）和软件插入“NOP”两种方法
  • 编译优化：通过编译器调整指令顺序来解决数据相关

数据冒险的分类：

• 写后读（RAW）相关：按序发射，按序完成时，只可能出现 RAW 相关

// R5 发生冲突
I1：ADD R5，R2，R4      (R2)+(R4) -> R5 // 往 R5 写入
I2：ADD R4，R5，R3      (R5)+(R3) -> R4 // 从 R5 读出

• 读后写（WAR）相关：乱序发射，编写程序的时候希望 I1 在 I2 前完成，但优化手段导致 I2 在 I1 前发射

// 编译优化后，导致 I2 先执行，I1 后执行，R2 发生冲突
// 或 I2 可能比 I1 先完成，导致 M 存储的是 (R4)+(R5) 的结果，而不是原本 R2 的值
I1: STA M，R2           (R2) -> M, M 为主存单元
I2: ADD R2，R4，R5      (R4)+(R5) -> R2

• 写后写（WAW）相关：存在多个功能部件时，后一条指令可能比前一条指令先完成

// I2 可能比 I1 先完成，导致 R3 最后存储的是 (R2)*(R1) 的结果，而不是 (R4)-(R5) 的结果
I1: MUL R3，R2，R1      (R2)*(R1) -> R3
I2: SUB R3，R4，R5      (R4)-(R5) -> R3

结构冒险（资源冲突）

• 概念：由于多条指令在同一时刻争用同一资源而形成的冲突称为结构相关
• 解决办法：
  • 暂停流水线：后一相关指令暂停一个时钟周期
  • 资源重复配置：数据存储器 + 指令存储器

控制冒险

• 概念：当流水线遇到转移指令和其他改变 PC 值的指令而造成断流时，会引起控制相关
• 解决办法：
  • 转移指令分支预测：简单预测（永远猜 true 或 false）、动态预测（根据历史情况动态调整）
  • 预取转移成功和不成功两个控制流方向上的目标指令
  • 加快和提前形成条件码
  • 提高转移方向的猜准率

---

问题三、简述一下指令执行的阶段

1. 取指(IF)：读取指令
2. 译码/读寄存器(ID)：译码 + 读取寄存器中的操作数
3. 执行/计算地址（EX）：执行运算操作或计算地址
4. 访存(MEM)：写回内存
5. 写回(WB)：写回寄存器堆

---

I/O方式

程序中断方式

问题一、中断优先级

中断优先级包括中断响应优先级与中断处理优先级

• 中断响应优先级：实际 CPU 响应中断请求的先后顺序，由硬件排队器实现，其无法被改变。
• 中断处理优先级：改优先级更高的中断会优先被处理，中断处理优先级可以由中断屏蔽字来改变。

【注意】

​

每一个中断源都有一个中断请求标记触发器与中断屏蔽触发器

• 中断请求触发器为“1”时，表示中断源有请求
• 中断屏蔽触发器为“1”时，表示屏蔽该中断源的请求。

中断屏蔽触发器可以实现：中断处理优先级调整、多重中断。

问题二、CPU响应中断的条件

1. 中断源有请求
2. CPU 开中断（异常和不可屏蔽中断不受其限制）
3. 处于中断周期

问题三、中断过程

一个完整的中断过程包括中断响应过程和中断处理过程。

中断响应过程

此过程由硬件自动完成，又称为中断隐指令，它并不是一条具体的指令，其过程如下：

• 关中断：保护断点和转移到中断服务程序的操作必须一气呵成，不能被再次中断。
• 保存断点：将原程序的断点存入堆栈或主存指定单元。
• 引出中断服务程序：识别中断源，取出中断服务程序的入口地址并传送给程序计数器（PC）。

注意几个要点

（1）断点、现场：

• 断点信息：指令无法读取的寄存器内容，如 PC、PSW 的内容。发生中断时，它们由硬件自动完成保护。
• 现场信息：指令可以读取的寄存器内容，如通用寄存器等。发生中断时，它们由软件（即程序员）完成保护，通常由中断服务程序中的指令把它们存入堆栈或主存指定单元。

（2）引出中断服务程序（硬件向量法之中断向量法）的过程：

识别中断源–>中断类型号–（中断向量地址形成部件）–>中断向量地址–>中断向量–>中断服务程序入口

（3）中断向量地址、中断向量、中断向量法、向量中断：

• 中断向量地址：中断向量表的各个表项的地址，即中断服务程序的指针的指针（存放中断向量的地址）。
• 中断向量：中断向量表的各个表项的内容，指向中断服务程序的入口，即中断服务程序的指针。
• 中断向量法：这种中断方法被称为中断向量法。
• 向量中断：采用中断向量法的中断被称为向量中断。

下面是一张中断向量表：

中断向量地址（中断向量的存储地址）	中断向量（指向中断服务程序的入口）
0000 0000H	1234 5678H
0000 0004H	6666 8888H
0000 0008H	4567 8901H
…	…

中断处理过程

此过程由**中断服务程序（软件）**完成，其过程如下：

• 保护现场和屏蔽字：保存通用寄存器和状态寄存器的内容。
• 开中断：允许更高优先级中断请求得到响应，实现中断嵌套。
• 执行中断服务程序：中断主体部分。
• 关中断：恢复现场的操作必须一气呵成，不能被再次中断。
• 恢复现场：恢复原来通用寄存器和状态寄存器的内容。
• 开中断、中断返回：通过中断返回指令回到原程序断点处，执行该指令时，硬件自动恢复断点信息。

DMA方式

DMA 传送过程

（1）预处理：

• DMA 控制器（DMAC）接受外设发出的 DMA 请求（外设传送一个字的请求），并向 CPU 发出总线请求。
• CPU 响应此总线请求，发出总线响应信号，DMA 控制器将接管 CPU 的地址总线、数据总线和控制总线，CPU 的主存控制信号被禁止使用。

（2）数据传送：

• CPU 向 DMA 控制器指明传送数据的主存单元地址及长度，以及数据在主存和外设间的传送方向。
• DMA 控制器发出读写等控制信号，执行数据传送操作。每传送一个数据，自动修改主存地址计数和传送长度计数。

（3）后处理：

• DMA 控制器向 CPU 报告 DMA 操作的结束，执行中断服务程序。恢复 CPU 的一切权利。

DMA 传送方式

主存和 DMA 控制器 之间有一条数据通路，不通过 CPU。但当 I/O 设备和 CPU
同时访问主存时，可能发生冲突，为了有效地使用主存，DMA 控制器与 CPU 通常采用以下 3 种方法使用主存：

• 停止 CPU 访问主存：CPU 处于不工作状态，未充分发挥 CPU 对主存的利用率。
• DMA 与 CPU 交替访存：一个 CPU 周期，分为 C1 和 C2 两个周期，C1 专供 DMA 访存，C2 专供 CPU 访存。
• 周期挪用（周期窃取）：DMA 访存时有三种可能：CPU 此时不访存（不冲突）；CPU 正在访存（存取周期结束让出总线）；CPU 与 DMA 同时请求访存（I/O 访存优先）。

【注意】这里的周期指的是存取周期！

​

DMA 控制器：对传送过程进行控制的硬件

DMA、Cache、通道均为硬件

DMA 方式与中断方式的比较

项目	中断方式	DMA 方式
数据传送	程序控制（程序的切换–>保存和恢复现场）	硬件控制（CPU只需进行预处理和后处理）
中断请求	传送数据	后处理
响应	指令执行周期结束后响应中断	每个机器周期结束均可，总线空闲时即可响应 DMA 请求
场景	CPU控制，低速设备	DMA控制器控制，高速设备
优先级	优先级低于DMA	优先级高于中断
异常处理	能处理异常事件	仅传送数据

操作系统

操作系统组成

中断与异常

中断与异常的概念

• 中断(Interruption) 也称外中断，指外部事件打断了CPU正在执行的程序的执行流程，使得CPU需要立即响应事件，执行特定的操作。

• 异常(Exception) 也称内中断，是指来自CPU执行指令内部的事件。

中断与异常的分类

• 中断包括：可屏蔽中断（INTR）和不可屏蔽中断（NMI）
• 异常包括：故障（Fault）、自陷（Trap）、终止（Abort）。故障是由指令执行时引起的异常，例如缺页故障、除数为0，自陷是一种是先安排好的“异常”事件，而终止是出现了使 CPU 终止的硬件故障。

异常种类	例子
故障（软件中断）	非法操作码、访存缺段、访存缺页、地址越界、除数为 0、浮点运算上溢
自陷（软件中断）	通过执行陷入指令来进行系统调用，此时 CPU 从用户态陷入到内核态；调试、断点事件；访管指令或陷入指令
终止（硬件中断）	控制器出错、存储器校验错

【注意】

• 异常不可被屏蔽。
• Cache 缺失不会引起异常，因为 Cache 缺失和虚拟存储器缺页缺段不是一个原理。
• 软件中断又称为程序性异常。

中断与异常的响应时间

• 中断：只能在指令周期中的中断周期被响应，即一条指令的最后
• 异常：能够在发起异常的下一个时钟周期就得到响应，应该是很快或者是立刻。

中断与异常的返回位置

• 中断：返回下一条指令
• 异常：故障返回当前指令，自陷返回下一条指令，终止无法执行指令。

---

内核态与用户态

**内核态（Kernel Mode）**与 用户态（User Mode）：是CPU运行的两种模式。

• 内核态是操作系统核心代码运行的特权级别。在内核态中，操作系统有完全的访问权限和控制权限，可以执行任意指令、使用任意寄存器、访问系统内存和硬件资源。内核态可以执行系统级别的操作，如创建和销毁进程、分配内存、读写硬件设备等等。由于内核态具有最高的特权级别，因此在该模式下执行的代码具有非常高的安全风险，因此只有操作系统核心代码可以运行在内核态中。
• 用户态是应用程序运行的特权级别。在用户态中，应用程序只能访问到分配给它的资源和内存，不能直接访问系统内存或硬件资源。应用程序不能执行特权指令或系统调用，这些操作只能通过操作系统提供的接口来实现。用户态运行的程序具有较低的特权级别，因此不能访问内核态中的数据或资源。

CPU工作状态的切换：

• 用户态 -> 内核态：通常是使用访管命令实现，也就是常说的陷入机制。同时还可以通过中断、异常来实现切换。

• 内核态 -> 用户态：由一条改变 psw(程序状态字寄存器) 值的特权指令来实现。

---

微内核（Micro kernel）

微内核是操作系统的一种内核架构模式，相较于宏内核，在微内核架构的操作系统中，只有操作系统的核心功能例如：时钟管理、中断处理、原语操作被放入内核内部，而例如进程管理、存储管理、设备管理等功能则在用户态中实现。

微内核具有更高的可扩展性与可靠性，操作系统中一个模块的崩溃并不会导致整个操作系统的崩溃，同时微内核还是采用客户/服务器模式，内核看做客户端，用户态的进程看做服务器端，两者通过消息传递机制实现通信。

但是相较于宏内核设计模式，微内核服务的实现需要频繁切换用户态与核心态，且用户态的各个功能模块不能直接调用，而是通过内核的"消息传递机制"实现，这回导致相较于宏内核架构模式，微内核的性能更低。

---

线程进程

问题1、进程和程序的比较

• 程序是存放在文件系统的比特信息，是永存的；而进程是暂时的，是程序在数据集上的一次执行；
• 程序是静态的观念；进程是动态的观念，其可以被创建、阻塞、终止。
• 进程具有并发性，而程序没有；
• 进程是计算机资源的分配基本单位，程序不是。

---

问题2、什么是进程,什么是线程?

进程是操作系统中资源分配基本单位，表示一个正在运行的应用程序或任务。每个进程都有一个独立的地址空间，可以独立地运行并占用系统资源。

线程是操作系统中的调度单位，是程序执行流的最小单元。每个线程有独立的程序计数器、调用栈和寄存器，但共享同一进程的其他资源。

进程与线程的区别在于，进程是独立的资源分配单位，线程是进程的一部分，是进程内部的执行流。因此，创建和管理进程的代价比较大，但每个进程独立运行，它们之间互不干扰。而创建和管理线程的代价较小，但它们共享同一进程内的资源，如果一个线程发生异常，可能会影响到其他线程的正常运行。

补充 : 父子进程可以共享资源但不共享存储空间，而进程与线程既可以共享资源也可以共享空间。

---

问题3、有了进程为什么需要线程?

答 ：在引入线程之前，进程是操作系统中资源分配和调度的基本单位，它可以独立运行并占用系统资源，但是进程的创建和切换都是有代价的，因此，对于一些需要高效执行的任务，如果使用进程进行处理，就可能带来较大的开销。

引入线程之后，线程是进程的一个执行单元，它成为了调度的基本单位，它可以共享进程的资源，而不需要独占系统资源，因此创建和切换线程的开销要远小于进程。同时，由于线程的轻量级特性，系统可以快速切换线程，从而使程序具有较好的响应速度。

---

问题4、同步互斥机制遵循的原则

答：1、空闲让进 2、忙则等待 3、有限等待 4、让权等待

---

问题5、死锁

• 死锁的定义：两个或多个进程因竞争资源或者互相等待对方释放资源而造成的一种僵局现象。。在死锁状态下，进程们会一直等待对方释放资源，不能继续执行，占用的系统资源也无法释放，导致系统长时间处于不可用状态。

• 死锁产生的原因：互斥、不可剥夺、请求与保持、循环等待。

• 死锁解除的方式：

  • 死锁预防：破坏互斥条件（不可行），破坏不可剥夺条件（请求得不到满足时放弃所有不可剥夺资源），破坏请求与保持条件（一次分配所有进程需要的资源），破坏循环等待条件（顺序资源分配法，只能按照编号递增的顺序分配资源）
  • 死锁避免：银行家算法判断分配后是否处于系统安全状态
  • 死锁检测 + 死锁解除：利用资源分配图检测死锁，利用资源剥夺、进程撤销、进程回退的方式解除死锁。

内存管理

程序装入步骤

• 预处理：预处理器可以删除注释、包含其他文件以及执行宏替代。
• 编译：编译预处理修改后的源文件生成编译程序文本(.s)。
• 汇编：汇编器将生成的汇编语言代码翻译为二进制目标程序(.o)。
• 链接（生成逻辑地址）：将一个或多个由编译器或汇编器生成的目标文件外加库链接为一个可执行文件(.exe)。链接方式有：
  • 静态链接：运行前先将目标模块连接成一个完整的配置模块并不会再次拆开。
  • 装入时链接：在装入内存时，采用边装入，边链接的方式。
  • 运行时链接：当目标模块被使用时，才会将目标模块装入。
• 装入（生成物理地址）：装入方式：
  • 绝对装入：只适用于单道程序，连接结束后将程序驻留在与逻辑地址相同的内存地址上不在变动。
  • 静态重定位：在装入时修改程序的指令和数据的地址，没有足够的内存空间就无法装入。
  • 动态重定位：装入内存的程序其所有地址为相对地址，当程序真正执行时再通过定位寄存器计算物理地址，只需要装入一部分程序即可投入运行。

文件管理

文件系统

问题一、文件系统的定义

文件系统是指一种组织和管理计算机存储设备上文件和目录的方式。它提供了一种标准化的方法来存储、访问、管理和维护文件和目录，使得用户可以方便地访问和管理存储在存储设备上的数据，磁盘上的每一个分区都可以拥有独自的文件系统。

常见的文件系统包括FAT、NTFS、EXT2/EXT3、HFS+等。

问题二、虚拟文件系统的定义

虚拟文件系统是一种抽象层，用于在操作系统中提供文件系统的统一接口。它可以让操作系统支持多种文件系统，并且使得不同的文件系统可以共享同一组API，使得用户和应用程序可以使用相同的接口来访问不同类型的文件系统。

虚拟文件系统向上层提供了统一的标准的系统调用接口，并要求下层的文件系统必须实现某些规定的函数功能。

问题三、操作系统的引导流程

1. CPU激活：激活CPU读取ROM中的boot程序，将指令寄存器设置为BIOS的第一条指令，执行BIOS程序。
2. BIOS自检：随后BIOS会进行自检，检查硬件设备是否正常。
3. MBR（主引导记录）程序加载：BIOS会查找硬盘的MBR 区域，并将MBR中的引导程序加载到内存中。MBR的作用是去告诉CPU去硬盘的哪一个分区去找操作系统。
4. PBR（分区引导记录）程序加载：读取活动分区的第一个扇区，这个扇区就是分区引导记录（PBR），其作用是寻找并激活分区根目录下用于引导操作系统的程序。
5. 内核初始化：内核加载完成后，会进行一些初始化操作，例如初始化设备驱动程序、建立进程、创建根文件系统等。
6. 用户空间初始化：内核初始化完成后，会创建第一个用户进程，并将控制权转移给用户进程，从而进入用户空间。

计算机网络

HTTP协议

您输入 URL 时，发生了哪些事？

1. 域名解析：浏览器首先将URL中的域名部分解析成IP地址。浏览器会先查找本地缓存中是否有该域名对应的IP地址，如果没有则会向本地DNS服务器发送查询请求。如果本地DNS服务器缓存中没有该域名对应的IP地址，则会向根域名服务器发送请求，逐级查询直到找到该域名对应的IP地址。
2. 建立TCP连接：一旦浏览器获得了目标服务器的IP地址，它就会使用TCP协议建立与服务器的连接。在建立TCP连接时，浏览器和服务器之间会进行三次握手，确保双方可以可靠地通信。
3. 发送HTTP请求：TCP连接建立后，浏览器会向服务器发送HTTP请求，其中包括请求方法（GET、POST等）、请求头和请求体等信息。请求头包括浏览器类型、所接受的数据格式等信息。
4. 服务器处理请求并返回响应：服务器收到浏览器发送的请求后，会根据请求中的信息进行处理，比如查询数据库、读取文件等操作。服务器处理完请求后，会将处理结果打包成HTTP响应发送回浏览器。
5. 浏览器渲染页面：浏览器接收到服务器返回的响应后，会根据响应中的内容渲染出页面。渲染页面的过程包括解析HTML、CSS和JavaScript等文件，构建DOM树和渲染树等步骤。
6. 断开TCP连接：一旦页面渲染完毕，浏览器会关闭与服务器的TCP连接，页面加载完成。

---

HTTP协议中 get 与 post 方法有何不同

HTTP协议中，GET和POST方法是最常用的两种请求方法，它们在以下几个方面有所不同：

1. 数据位置：GET方法将请求数据包含在URL中，而POST方法将请求数据包含在请求体中。因此，GET方法的请求数据会被浏览器缓存，而POST方法的请求数据不会被缓存。
2. 数据长度限制：由于GET方法的数据包含在URL中，因此URL的长度受到限制。不同浏览器的限制长度不同，但通常在2048个字符左右。而POST方法的数据可以放在请求体中，因此可以包含更多的数据，通常没有长度限制。
3. 安全性：GET方法将请求数据暴露在URL中，因此不安全，容易被拦截、篡改。而POST方法将请求数据包含在请求体中，不容易被拦截和篡改，因此安全性更高。
4. 使用场景：通常来说，GET方法适合用于获取数据，比如搜索、过滤、排序等操作。而POST方法适合用于提交数据，比如表单提交、文件上传等操作。

总的来说，GET方法适用于对数据进行查询操作，请求数据量小，对安全性要求不高的场景；而POST方法适用于对数据进行增删改操作，请求数据量大，对安全性要求较高的场景。

数据结构

树

树的基本概念

1. 树的基本概念：树是由若干个结点组成的一种层次结构，其中一个结点为根结点，每个结点可以有零个或多个子结点。结点之间的连线称为边，根结点没有父结点，而其他结点都有一个父结点。
2. 树的遍历：树的遍历是指按照某种规则依次访问树的所有结点。常见的树的遍历方式有前序遍历、中序遍历和后序遍历。此外，还有层次遍历等方式。
3. 二叉树的基本概念：二叉树是一种特殊的树，每个结点最多有两个子结点，分别称为左子结点和右子结点。二叉树有多种类型，例如满二叉树、完全二叉树等。
4. 二叉树的遍历：二叉树的遍历方式包括前序遍历、中序遍历、后序遍历和层次遍历。其中前序遍历、中序遍历和后序遍历通常也被称为深度优先遍历。
5. 完全二叉树：完全二叉树是一种特殊的二叉树，其中除了最后一层节点可能不满，其他层节点都是满的，而且最后一层节点都靠左排列。
6. 平衡树：平衡树是一种特殊的二叉搜索树，它保证在树中查找、插入、删除等操作的时间复杂度为 O(logn)。常见的平衡树包括红黑树、AVL树等。

二叉树的存储方式

二叉树的存储方式有：顺序存储方式与链式存储方式。

顺序存储方式：

链式存储方式：

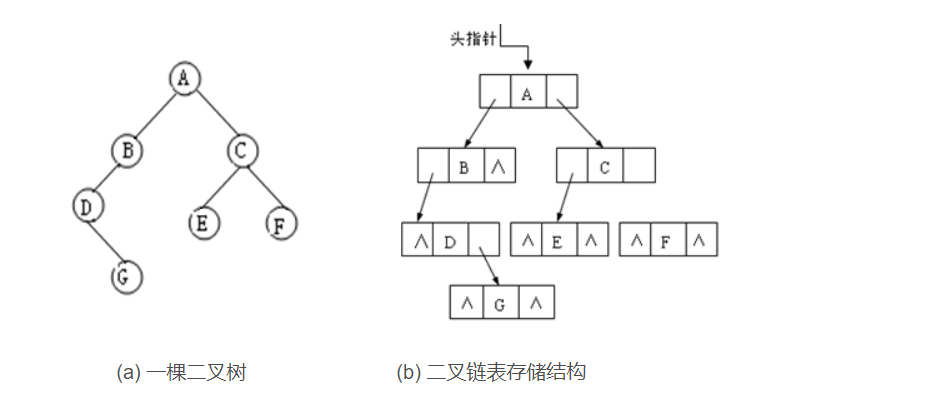
树的存储方式

树的存储方式主要有：双亲表示法、孩子表示法、孩子兄弟表示法

平衡二叉树

平衡二叉树的插入、删除的调整动作，每次调整的对象都是最小不平衡子树，即从插入节点开始向根节点方向的第一个不平衡节点以该节点为根节点的子树！插入操作步骤如下：

1. 首先，需要将要插入的节点插入到二叉搜索树中的合适位置，与非平衡二叉树的插入操作相同。
2. 然后，需要检查插入节点的祖先节点是否平衡。具体来说，从插入节点开始，向上回溯到根节点，每经过一个节点就计算一下它的左右子树的高度差，如果高度差大于1，那么这个节点为根的子树为最小不平衡子树（记为A节点)。
3. 如果某个节点不平衡，就需要进行旋转操作来恢复平衡。旋转操作分为左旋和右旋，具体操作如下：
   • 如果在新插入的节点在A节点左孩子的左子树上，则需要右旋 （LL）
   • 如果在新插入的节点在A节点右孩子的右子树上，则需要左旋 （RR）
   • 如果在新插入的节点在A节点左孩子的右子树上，则需要左旋后以对新的最小不平衡子树右旋 （LR）
   • 如果在新插入的节点在A节点右孩子的左子树上，则需要右旋后以对新的最小不平衡子树左旋 （LR）

B树与B+树（详细见书本）

---

图

Dijkstra算法

Dijkstra常常用于解决单源的最短路径问题，时间复杂度为：$n\ast logn$，核心思路是贪心算法。

• 参数需求：
  • path：存储点与点的路径关系，点与点之间无法直接到达距离为INF
  • from：起点索引位置
  • to：终点索引位置
• 功能描述：
  • 从from点到to点的最短距离，如果无法到达则返回 -1

Dijkstra算法无法处理边上带有负权值的情况

final int INF = Integer.MIN_VALUE / 2;

public int dijstra(int path[][], int from, int to) {
    int n = path.length;
    //dist[]保存距离的最小值
    int[] dist = new int[n];
    //used存储使用情况
    boolean[] used = new boolean[n];
    //初始化
    Arrays.fill(dist, INF);
    dist[from] = 0;
    //开始遍历
    //为什么是 0 ~ n - 1 遍历呢，为了解冗余处理 from 节点的情况，初始化dist与used数组
    for (int i = 0; i < n; i++) {
        //存储下一个结点编号
        int x = -1;
        //遍历寻找最短且没有被使用的结点
        for (int y = 0; y < n; y++) {
            if (!used[y] && (x == -1 || dist[y] < dist[x])) {
                x = y;
            }
        }
        used[x] = true;
        //更新距离
        for (int iz = 0; iz < n; iz++) {
            dist[iz] = Math.min(dist[iz], path[x][iz] + dist[x]);
        }
    }
    int ans = -1;
    for (int val : dist) {
        ans = Math.max(ans, val);
    }
    return ans == INF ? -1 : ans;
}

Floyd算法

Floyd常常用于解决多源最短路径问题，时间复杂度为：$O(N^3)$

• 参数需求：
  • path：存储点与点的路径关系，点与点之间无法直接到达距离为INF
• 功能描述：
  • 将path数组存储所有点到目标点的最短距离，如果无法到达值为INF

Floyd算法允许途中带有权值为负数的边，但是不允许含有负权值边组成的回路

final int INF = Integer.MIN_VALUE / 2;

// 该版本path数组会被修改
public void floyd(int path[][]) {
    int n = path.length;
    for (int z = 0; z < n; ++z) {
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                path[i][j] = Math.min(path[i][j], path[i][z] + path[z][j]);
            }
        }
    }
}

---

查找算法

---

排序算法

排序算法代码

1、冒泡排序

public static void bubbleSort(int[] arr) {
    int n = arr.length;
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < n - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

2、选择排序

void selectionSort(int[] arr) {
    int n = arr.length;
    for (int i = 0; i < n - 1; i++) {
        int minIndex = i;
        for (int j = i + 1; j < n; j++) {
            if (arr[j] < arr[minIndex]) {
                minIndex = j;
            }
        }
        int temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
}

3、插入排序

public void insertionSort(int[] arr) {
    int n = arr.length;
    for (int i = 1; i < n; i++) {
        int key = arr[i];
        int j = i - 1;
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = key;
    }
}

4、快速排序

    public void quickSort(int[] nums, int left, int right) {
        if (left >= right) {
            return;
        }
        // 快排优化：随机让数组中的一个元素与 nums[left] 交换
        int pivot = nums[left];
        int i = left;
        int j = right;
        while(i < j) {
            while (i < j && nums[j] >= pivot) {
                --j;
            }
            while(i < j && nums[i] <= pivot) {
                ++i;
            }
            if (i < j) {
                swap(nums, i, j);
            }
        }
        swap(nums, left, i);
        quickSort(nums, left, i - 1);
        quickSort(nums, i + 1, right);
    }

5、归并排序

public static void mergeSort(int[] arr, int left, int right) {
    if (left < right) {
        int mid = (left + right) / 2;
        mergeSort(arr, left, mid);
        mergeSort(arr, mid + 1, right);
        merge(arr, left, mid, right);
    }
}

public static void merge(int[] arr, int left, int mid, int right) {
    int[] temp = new int[right - left + 1];
    int i = left;
    int j = mid + 1;
    int k = 0;
    while (i <= mid && j <= right) {
        if (arr[i] <= arr[j]) {
            temp[k++] = arr[i++];
        } else {
            temp[k++] = arr[j++];
        }
    }
    while (i <= mid) {
        temp[k++] = arr[i++];
    }
    while (j <= right) {
        temp[k++] = arr[j++];
    }
    for (int p = 0; p < temp.length; p++) {
        arr[left + p] = temp[p];
    }
}

6、堆排序

public void heapSort(int[] arr) {
    int n = arr.length;

    // 构建大顶堆，如果 1 为开始下标，则 i = n / 2
    for (int i = n / 2 - 1; i >= 0; i--) {
        heapify(arr, n, i);
    }

    // 依次取出堆顶元素，放到末尾
    for (int i = n - 1; i > 0; i--) {
        // 将堆顶元素交换到末尾
        int temp = arr[0];
        arr[0] = arr[i];
        arr[i] = temp;

        // 对剩余元素进行堆化，重新构建大顶堆
        heapify(arr, i, 0);
    }
}

/**
 * 对以指定节点为根节点的子树进行堆化，使其满足大顶堆的性质
 * 
 * @param arr  待排序数组
 * @param n    堆的大小，需要堆化的元素个数
 * @param root 要堆化的子树的根节点
 */
private void heapify(int[] arr, int n, int root) {
    int largest = root; // 记录根节点、左子节点、右子节点中的最大值
    int left = 2 * root + 1;
    int right = 2 * root + 2;

    // 找出左子节点、右子节点、根节点中的最大值
    if (left < n && arr[left] > arr[largest]) {
        largest = left;
    }
    if (right < n && arr[right] > arr[largest]) {
        largest = right;
    }

    // 如果根节点不是最大值，则将根节点和最大值交换，并递归对子树进行堆化
    if (largest != root) {
        int temp = arr[root];
        arr[root] = arr[largest];
        arr[largest] = temp;
        heapify(arr, n, largest);
    }
}

排序算法时间复杂度

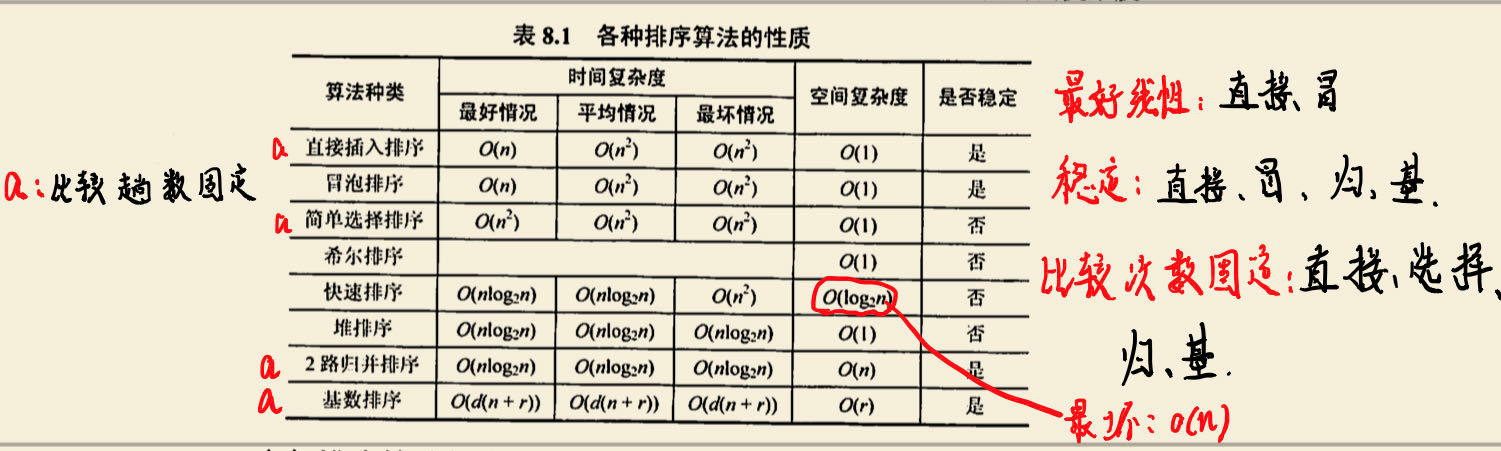
特殊情况处理：

• 对于大量的浮点数进行排序：优先考虑使用快速排序算法，因为快速排序算法的时间复杂度为 O(nlogn)，而且实际表现通常很好，在大多数情况下优于其他基于比较的排序算法。
• 对于已经排好序的数组：使用插入排序、冒泡排序算法的时间复杂度是 O(n)。
• 对于只包含0和1的数组：可以使用桶排序算法来对其进行排序，桶排序的时间复杂度为 O(n)。
• 对于1亿个数据数组选出前100大的数：使用堆排序，建立一个100大小的数组读出前100个数据，建立小顶堆，随后依次读入数据。若读入的数据小于堆顶的数则丢弃，否则用改数取代堆顶并重新调整堆，待数据读取完毕。