前言

如果你对这篇文章感兴趣，可以点击「【访客必读 - 指引页】一文囊括主页内所有高质量博客」，查看完整博客分类与对应链接。

在介绍模糊聚类之前，我们先简单地列举一下聚类算法的常见分类：

• 硬聚类 (Hard Clustering)
  • Connectivity-based clustering (Hierarchical Clustering)
  • Centroid-based Clustering (k-means clustering)
  • Distribution-based Clustering (Gaussian Mixture Model)
  • Density-based Clusterin (DBSCAN)
• 软聚类 (Soft Clustering)
  • Fuzzy Clustering

我们之前听说的大部分聚类算法均为硬聚类，即要求每个数据点只能属于一个特定的簇，scikit-learn 中有关于常见硬聚类算法的可视化展示，可供参考：

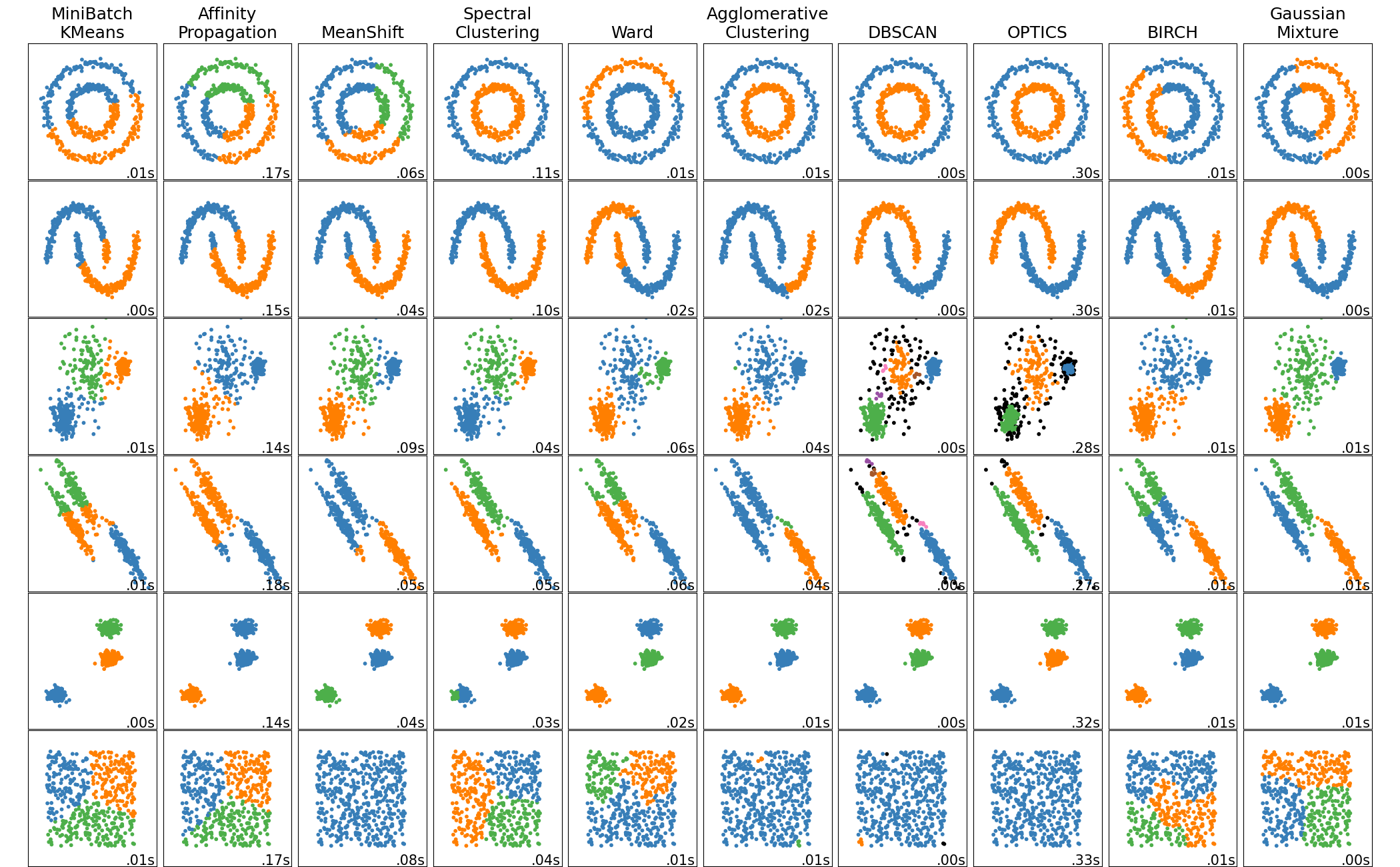
不同于硬聚类，软聚类放松了限制，即允许数据点可以同时属于多个簇。接下来要介绍的模糊聚类即为一种常见的软聚类算法。

---

模糊聚类

模糊聚类通常用一个向量来表示一个数据点的归属，向量中哪个维度的数值更大，意味着该数据点距离该维度对应簇更近，也可以理解为是归属于该簇的概率越大。

以 Fuzzy c-means (FCM) 聚类算法为例，其过程与 k-means 非常相似：

• 选择 $C$ 作为簇个数
• 随机赋予每个点归属于各个簇的概率向量 { w i } i = 1 N {\{\boldsymbol{w}_i\}}_{i=1}^N {wi​}i=1N​
• 迭代至收敛
  • 重新计算每个簇的簇中心 { c k } k = 1 C {\{\boldsymbol{c}_k\}}_{k=1}^C {ck​}k=1C​
  • 重新计算每个点归属于各个簇的概率向量 { w i } i = 1 N {\{\boldsymbol{w}_i\}}_{i=1}^N {wi​}i=1N​

簇中心 ${\mathbf{c}}_k$ 计算式如下：
$${\mathbf{c}}_k=\frac{{\sum }_{i=1}^N{w}_{i,k}^m{\mathbf{x}}_i}{{\sum }_{i=1}^N{w}_{i,k}^m},$$

其中 $m\in (1,\infty )$ 为超参，控制聚类的模糊程度，其数值越大，聚类结果越模糊，其数组越逼近 $1$， 其聚类效果越接近 k-means。

数据点 ${\mathbf{x}}_i$ 的概率向量 ${\mathbf{w}}_i$ 计算式如下：
$$w_{i,k}=\frac{1}{{\sum }_{j=1}^C{\left(\frac{\Vert {\mathbf{x}}_i-{\mathbf{c}}_k\Vert }{\Vert {\mathbf{x}}_i-{\mathbf{c}}_j\Vert }\right)}^{\frac{2}{m-1}}},$$

其满足 ${\sum }_{k=1}^C{w}_{i,k}=1$。FCM 整个聚类过程想要最小化的目标函数如下所示：
$$J(\mathbf{W},\mathbf{C})=\sum _{i=1}^N\sum _{k=1}^C{w}_{i,k}^m{\Vert {\mathbf{x}}_i-{\mathbf{c}}_k\Vert }^2.$$

---

参考资料

• wiki - Fuzzy clustering
• scikit-learn clustering