一.二分查找
前提:数组为有序数组,数组中无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的,这些都是使用二分法的前提条件,当题目描述满足如上条件的时候,可要想一想是不是可以用二分法了。
左必右闭写法
第一种写法,我们定义 target 是在一个在左闭右闭的区间里,也就是[left, right](这个很重要非常重要)。
区间的定义这就决定了二分法的代码应该如何写
因为定义target在[left, right]区间,所以有如下两点:
while (left <= right) 要使用 <= ,因为left == right是有意义的,所以使用 <=
if (nums[middle] > target) right 要赋值为 middle - 1,因为当前这个nums[middle]一定不是target,那么接下来要查找的左区间结束下标位置就是 middle - 1
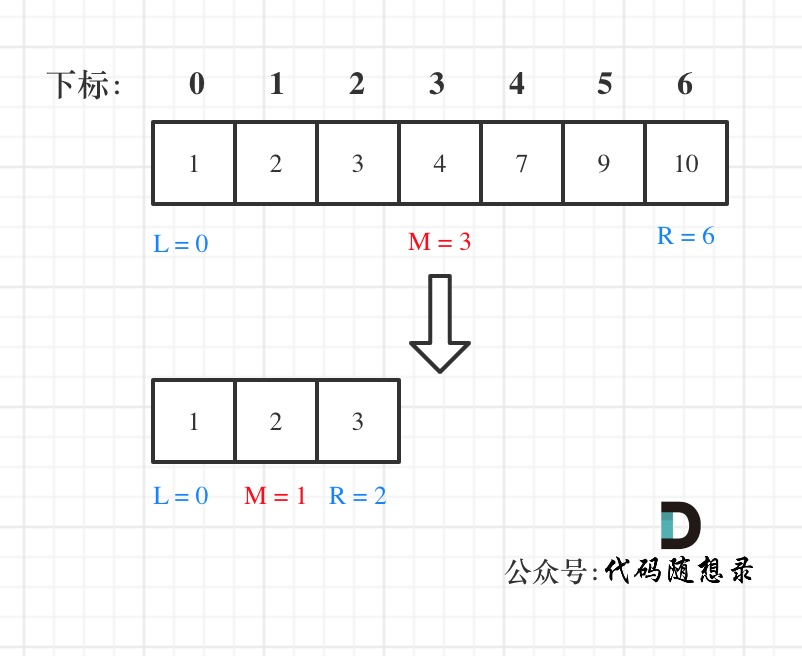
例如在数组:1,2,3,4,7,9,10中查找元素2,如图所示:
// 版本一
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]
while (left <= right) { // 当left==right,区间[left, right]依然有效,所以用 <=
int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
if (nums[middle] > target) {
right = middle - 1; // target 在左区间,所以[left, middle - 1]
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间,所以[middle + 1, right]
} else { // nums[middle] == target
return middle; // 数组中找到目标值,直接返回下标
}
}
// 未找到目标值
return -1;
}
};左闭右开写法
如果说定义 target 是在一个在左闭右开的区间里,也就是[left, right) ,那么二分法的边界处理方式则截然不同。
有如下两点:
while (left < right),这里使用 < ,因为left == right在区间[left, right)是没有意义的
if (nums[middle] > target) right 更新为 middle,因为当前nums[middle]不等于target,去左区间继续寻找,而寻找区间是左闭右开区间,所以right更新为middle,即:下一个查询区间不会去比较nums[middle]
在数组:1,2,3,4,7,9,10中查找元素2,如图所示:(注意和方法一的区别)
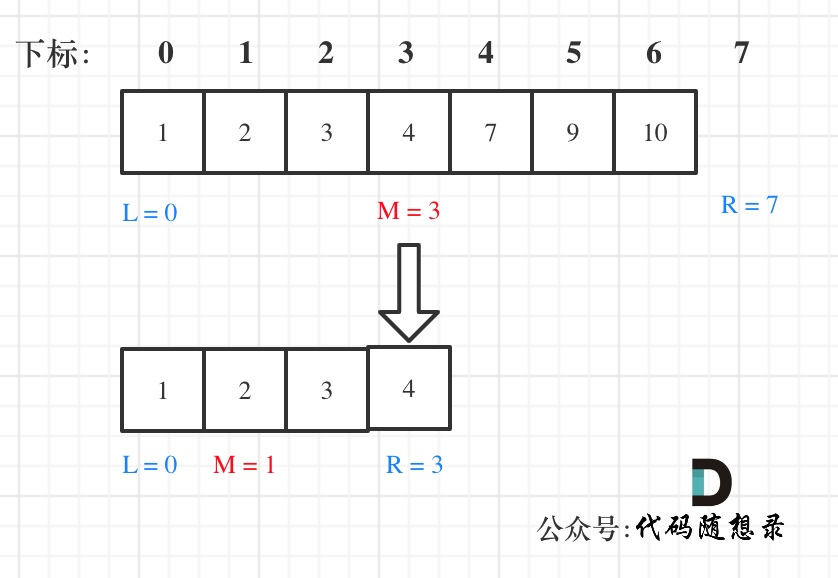
// 版本二
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size(); // 定义target在左闭右开的区间里,即:[left, right)
while (left < right) { // 因为left == right的时候,在[left, right)是无效的空间,所以使用 <
int middle = left + ((right - left) >> 1);
if (nums[middle] > target) {
right = middle; // target 在左区间,在[left, middle)中
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间,在[middle + 1, right)中
} else { // nums[middle] == target
return middle; // 数组中找到目标值,直接返回下标
}
}
// 未找到目标值
return -1;
}
};二.双指针法
双指针法基本都是应用在数组,字符串与链表的题目上
例题
27. 移除元素 - 力扣(Leetcode)
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。不要使用额外的数组空间, 你必须仅使用 O(1) 额外空间并原地修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1:
给定 nums = [3,2,2,3], val = 3, 函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。 你不需要考虑数组中超出新长度后面的元素。
示例 2:
给定 nums = [0,1,2,2,3,0,4,2], val = 2, 函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。
你不需要考虑数组中超出新长度后面的元素。
要知道数组的元素在内存地址中是连续的,不能单独删除数组中的某个元素,只能覆盖。
通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
定义快慢指针
快指针:寻找新数组的元素 ,新数组就是不含有目标元素的数组
慢指针:指向更新 新数组下标的位置
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int slow=0;//慢指针
int length=nums.size();
for(int fast=0;fast<length;fast++){//快指针
if(nums[fast]!=val){
nums[slow]=nums[fast];
slow++;
}
}
return slow;
}
};三.滑动窗口
1.1例题
209. 长度最小的子数组 - 力扣(Leetcode)
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组,并返回其长度。如果不存在符合条件的子数组,返回 0。
示例:
输入:s = 7, nums = [2,3,1,2,4,3] 输出:2 解释:子数组 [4,3] 是该条件下的长度最小的子数组。
提示:
1 <= target <= 10^9
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^5
解法:所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。其实滑动窗口也可以理解为双指针法的一种!只不过这种解法更像是一个窗口的移动,所以叫做滑动窗口更适合一些。
在本题中实现滑动窗口,主要确定如下三点:
窗口内是什么?
如何移动窗口的起始位置?
如何移动窗口的结束位置?
窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。
窗口的起始位置如何移动:如果当前窗口的值大于s了,窗口就要向前移动了(也就是该缩小了)。
窗口的结束位置如何移动:窗口的结束位置就是遍历数组的指针,也就是for循环里的索引。
解题的关键在于 窗口的起始位置如何移动
滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int i=0;
int j=0;
int sum=0,result=INT_MAX;
while(j<nums.size()){
sum+=nums[j];
while(sum>=target){
if(j-i+1<result)result=j-i+1;
sum-=nums[i];//必须先减再加
i++;
}
j++;
}
if(result==INT_MAX)return 0;
else return result;
}
};时间复杂度:O(n)
看每一个元素被操作的次数,每个元素在滑动窗后进来操作一次,出去操作一次,每个元素都是被操作两次,所以时间复杂度是 2 × n 也就是O(n)
空间复杂度:O(1)
1.2模板
关键字:满足XXX条件(计算结果,出现次数,同时包含)最长/最短 子串/子数组
例如:长度最小的子数组
//最长模板:
初始化left, right, result, bestResult
while (右指针没有到结尾) {
窗口扩大, 加入right对应元素, 更新当前result
while (result不满足要求) {
窗口缩小, 移除left对应元素, left右移
}
更新最优结果bestResult
right++;
}
返回bestResult;
//最短模板:
初始化left, right, result, bestResult
while (右指针没有到结尾) {
窗口扩大, 加入right对应元素, 更新当前result
while (result满足要求) {
更新最优结果bestResult
窗口缩小, 移除left对应元素, left右移
}
right++;
}
返回bestResult;