动态规划 背包问题

问题描述：
有一个背包，总容量为12。有6件物品，每件物品的重量和价值不同，求在背包总容量12的前提下，装进物品的最大价值以及装进物品的编号

单个物品重量和价值：

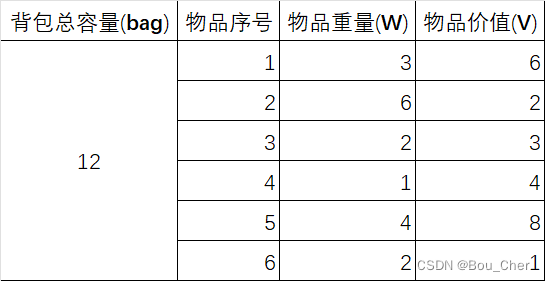
为方便进行思考，我们将物品按照重量价值递增，重新排序

---

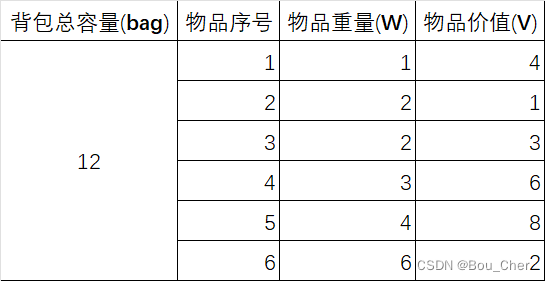
针对此问题，我们可以先列一张表格，标识当前背包容量为j时，前i个物品的最大价值。

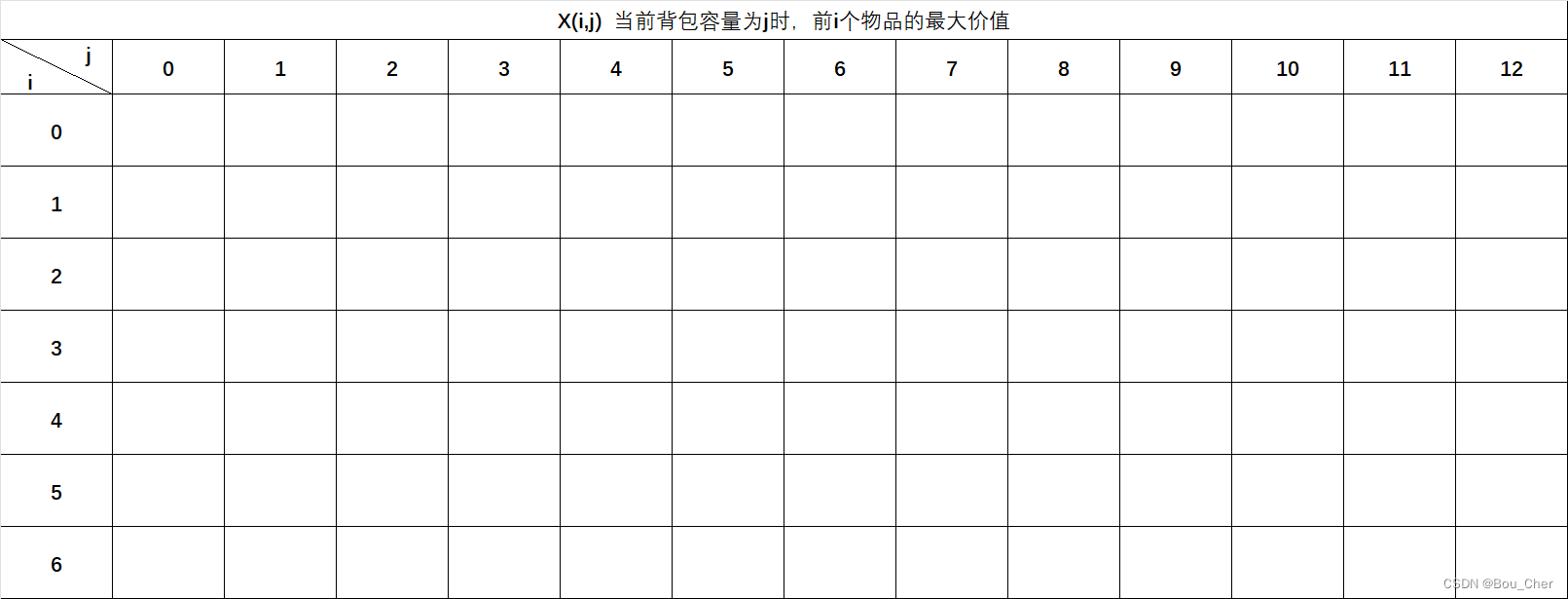
例如X(3,3)，代表当背包容量为3时，前3个物品可装入的最大价值。

---

第一行X(0,0)到X(0,12)，代表当背包容量为0到12时，前0个物品可装入的最大价值，前0个物品不存在没有价值，即价值恒为0，因此第一行都填入0。

同理第一列X(0,0)到X(6,0)，代表当背包容量为0时，第0个物品到第6个物品可装入的最大价值，因为背包容量为0，没有物品可以装下，所以第一列都填入0。

---

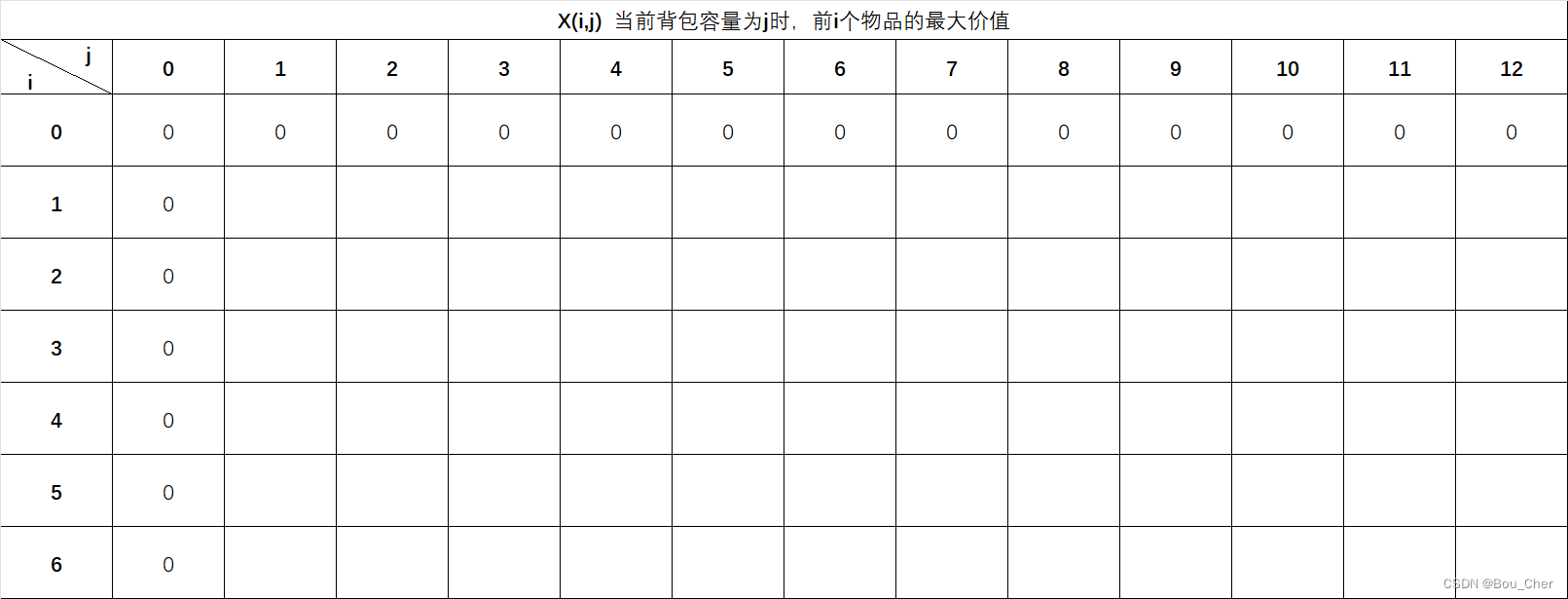
X(1,1) 代表当背包容量为1时，前1个物品的最大价值。由于W(1)=1，刚好可以装入，那么X(i,j)=X(1,1)=V(1)=4 ，因此填入4。并且不论之后背包容量如何扩展，前1个物品的最大价值恒为4。

---

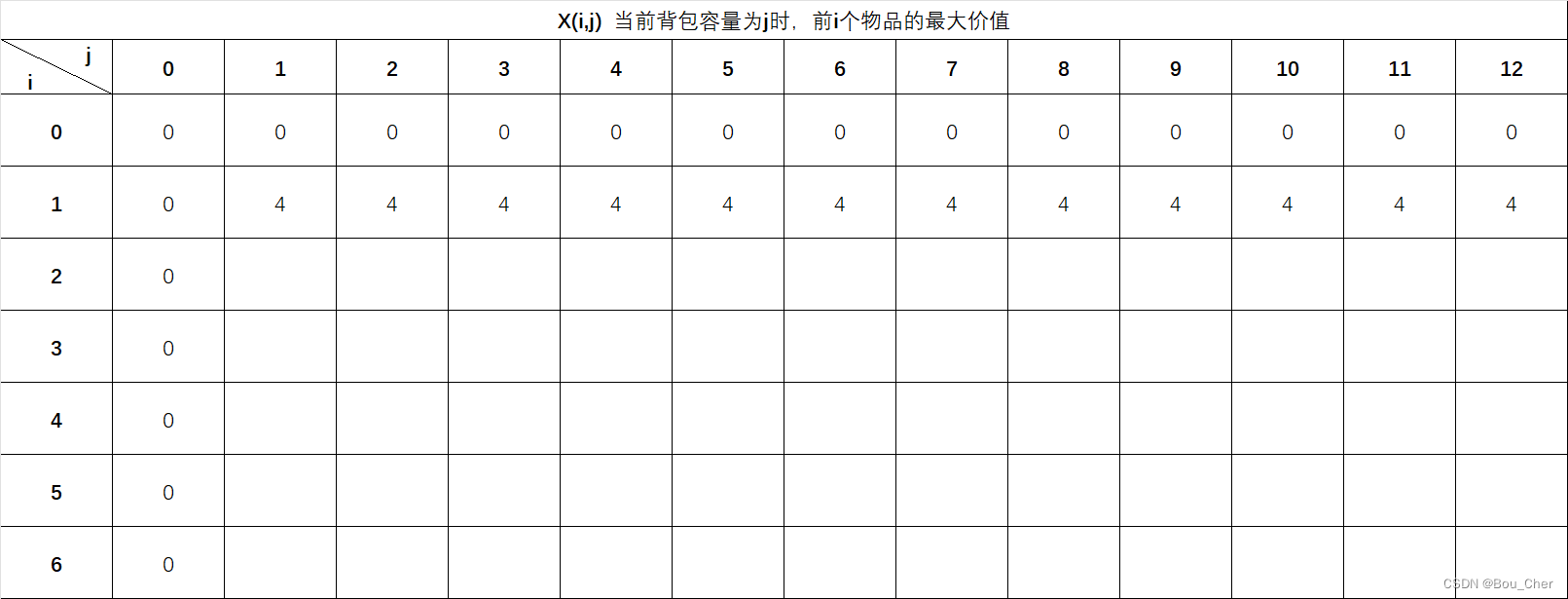
当开始第三行，即X(2,j) 填写时，就需要判断背包容量够不够装下当前物品，如果能装下，那装下当前物品和不装当前物品哪个价值最大：

1. 背包装不下：

   当背包容量j小于当前第i个物品重量W(i) 时，即j<W(i) 判断为装不下，此时的最大价值X(i,j) 与前一个X(i-1,j) 的最大价值一样，即X(i,j)=X(i-1,j)。

2. 背包装得下：

   当背包容量j大于等于当前第i个物品重量W(i) 时，判断要不要装进背包。

   2.1：装入当前物品时的最大价值Value1：
   背包总容量j减去当前物品的重量W(i) 后，获取剩余总容量的上一物品最大价值X(i-1,j-W(i)) 与当前物品的价值V(i) 相加，即 Value1=X(i,j-W(i)) + V(i) 。

   2.2：不装当前物品时的最大价值Value2：
   前一个物品i-1在此背包总容量j情景下的最大价值X(i-1,j)，即 Value2=X(i-1,j) 。

Value1-Value2 大于0则取当前和值Value1，反之取上一物品此背包总容量情景下的最大价值Value2。

此时不理解上述公式没关系，跟着下面的填数去慢慢理解

---

X(2,1) 填数，首先判断背包能否装下：

j=1，W(2)=2，j<W(2)，因此当背包容量为1时，物品2装不下，此时最大价值取前一个物品i-1此背包总容量j情景下的最大价值X(i-1,j)=X(2-1,1)=X(1,1)=4，因此X(2,1)=4。

---

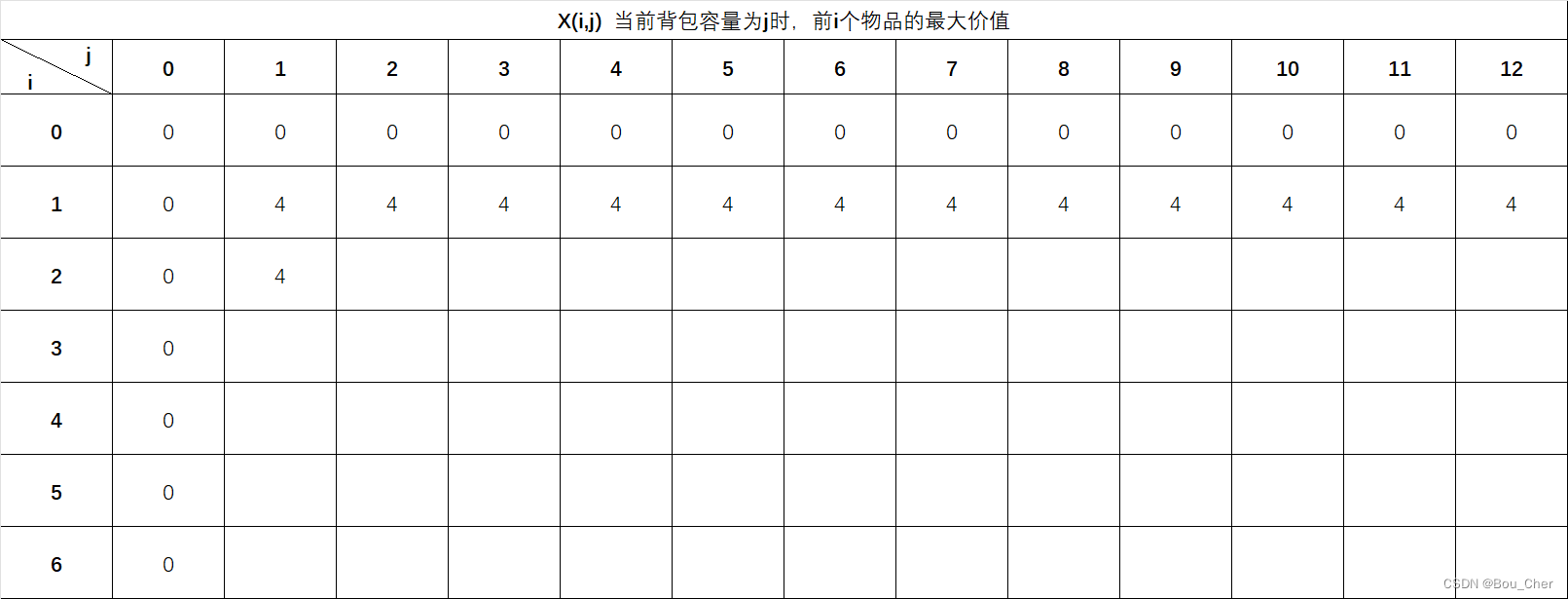
X(2,2) 填数，首先判断背包能否装下：

j=2，W(2)=2，j=W(2)，因此当背包容量为2时，物品2装得下。

此时需要判断要不要装物品2：

装入当前物品时的最大价值：Value1 = X(i-1,j-W(i)) + V(i) = X(2-1,2-2) + 1 = X(1,0) + 1 = 0 + 1 = 1。

不装当前物品时的最大价值：Value2 = X(i-1,j) = X(2-1,2) = X(1,2) = 4。

Value1<Value2，因此取上一物品此背包总容量情景下的最大价值，即X(2,2) = X(1,2) = 4。

---

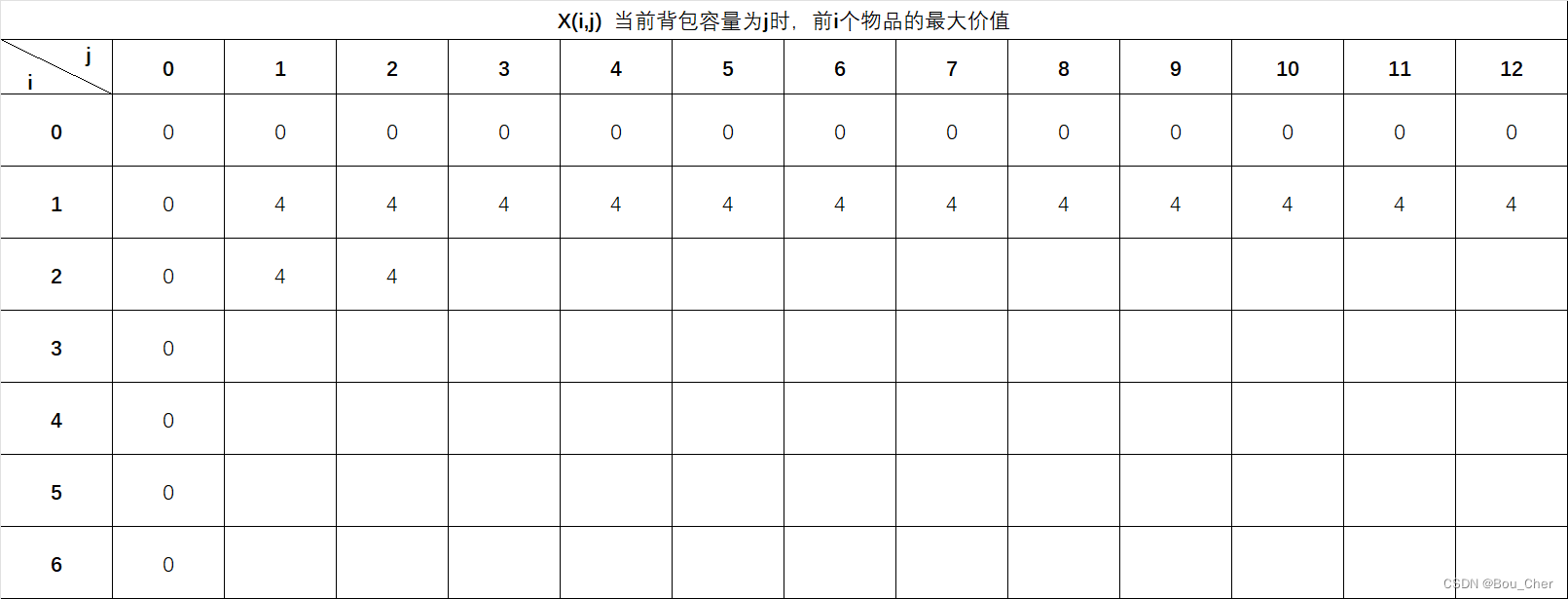
X(2,3) 填数，首先判断背包能否装下：

j=3，W(2)=2，j>W(2)，因此当背包容量为3时，物品2装得下。

此时需要判断要不要装物品2：

装入当前物品时的最大价值：Value1 = X(i-1,j-W(i)) + V(i) = X(2-1,3-2) + 1 = X(1,1) + 1 = 4 + 1 = 5。

不装当前物品时的最大价值：Value2 = X(i-1,j) = X(2-1,3) = X(1,3) = 4。

Value1>Value2，因此取当前物品的价值加剩余总容量的最佳价值，即X(2,3) = 5。

---

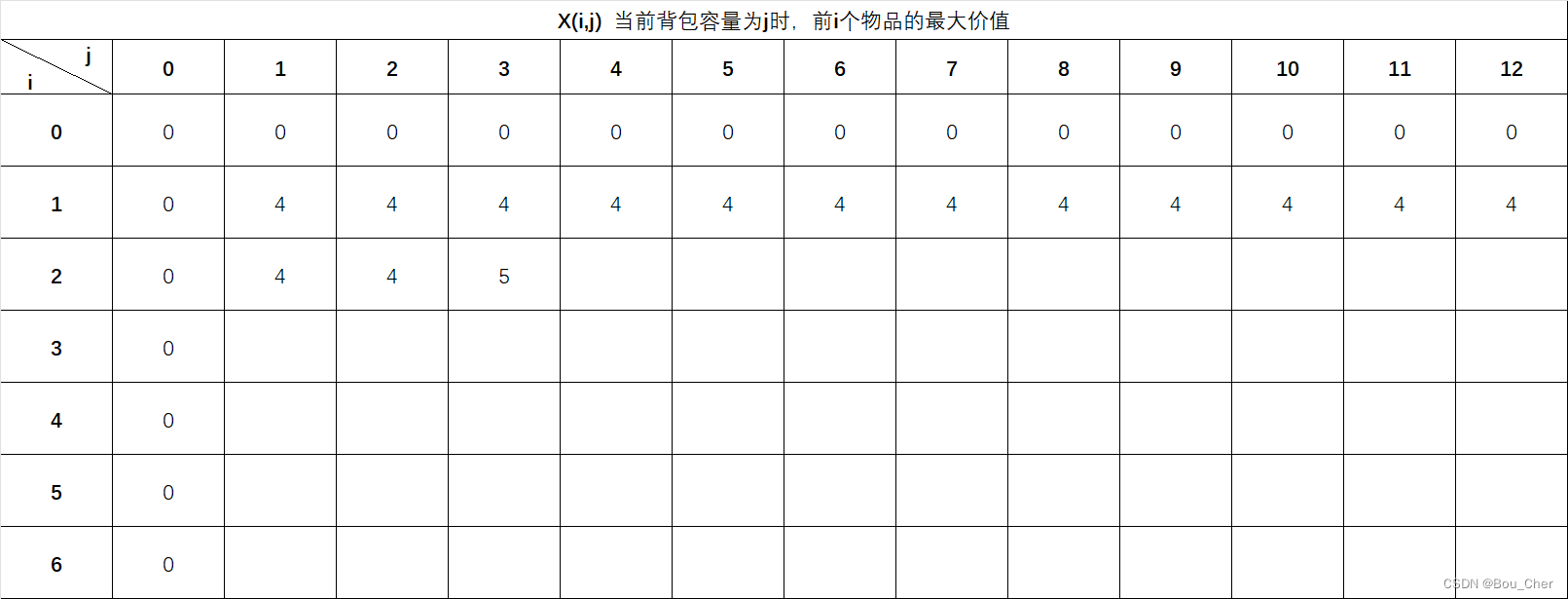
按照此规律，我们将表全部填充完毕：

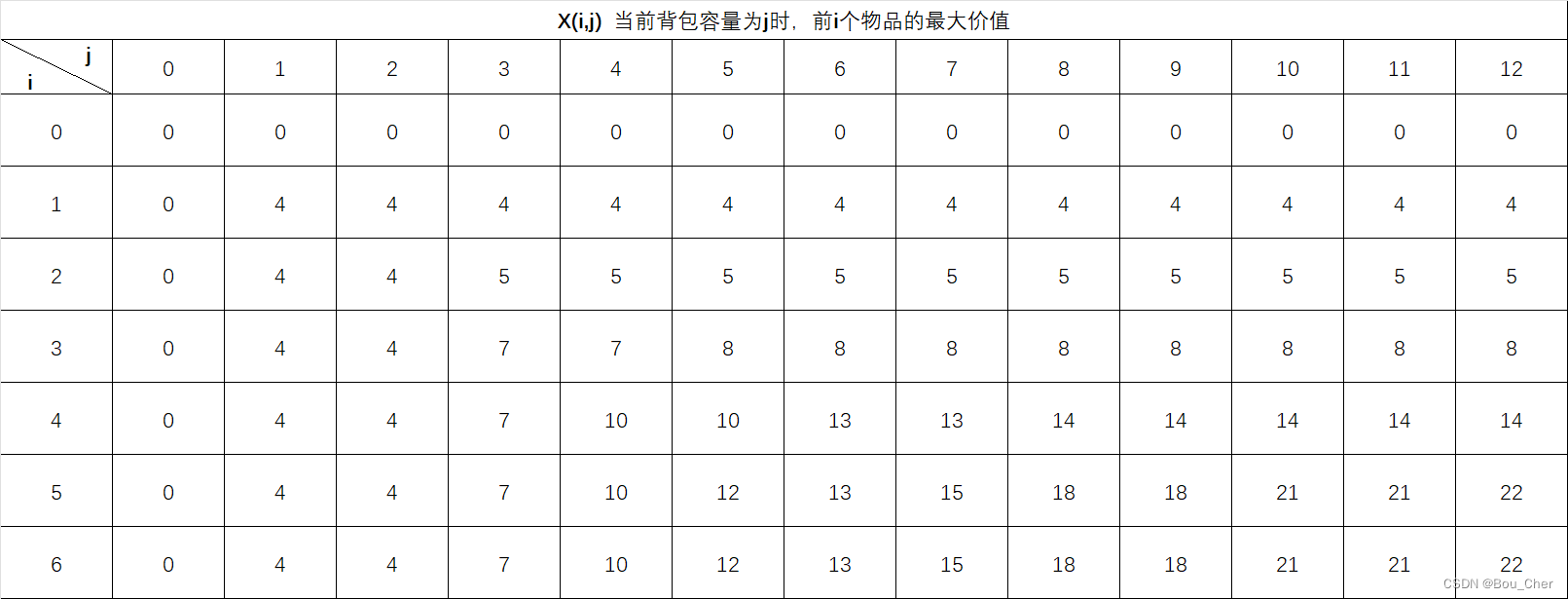
取两个坐标进行验证：

---

例如1：X(4,3) 填数，首先判断背包能否装下：

j=3，W(4)=3，j=W(4)，因此当背包容量为3时，物品4装得下。

此时需要判断要不要装物品4：

装入当前物品时的最大价值：Value1 = X(i-1,j-W(i)) + V(i) = X(4-1,3-3) + 6 = X(3,0) + 6 = 0 + 6 = 6。

不装当前物品时的最大价值：Value2 = X(i-1,j) = X(4-1,3) = X(3,3) = 7。

Value1<Value2，因此取上一物品此背包总容量情景下的最大价值，即X(4,3) = X(3,3) = 7。

---

例如2：X(4,4) 填数，首先判断背包能否装下：

j=4，W(4)=3，j>W(4)，因此当背包容量为4时，物品4装得下。

此时需要判断要不要装物品4：

装入当前物品时的最大价值：Value1 = X(i-1,j-W(i)) + V(i) = X(4-1,4-3) + 6 = X(3,1) + 6 = 4 + 6 = 10。

不装当前物品时的最大价值：Value2 = X(i-1,j) = X(4-1,4) = X(3,4) = 7。

Value1>Value2，因此取当前物品的价值加剩余总容量的最佳价值，即X(4,3) = 10。

---

代码实现：

int bag = 12; // 背包总容量
int number = 6; // 物品数量
int[] weight = {1, 2, 2, 3, 4, 6}; // 物品重量数组
int[] value = {4, 1, 3, 6, 8, 2}; // 物品价值数组
int[][] max = new int[number + 1][bag + 1]; // 最大价值数组

int value1 = 0; // 过渡值：装入当前物品时的最大价值
int value2 = 0; // 过渡值：不装当前物品时的最大价值

// 找出最大价值

for (int i = 1; i <= number; i++) { // 行
	for (int j = 1; j <= bag; j++) { // 列
		// 判断背包能否装得下
		if (j < weight[i - 1]) { // 装不下
			max[i][j] = max[i - 1][j]; // 与前一个物品的最大价值相同
		} else { // 能装下
			// 前一个物品剩余重量的最大价值+当前物品的价值
			value1 = max[i - 1][j - weight[i - 1]] + value[i - 1];
			// 前一个物品当前重量的最大价值
			value2 = max[i - 1][j];
			// 取最大值
			max[i][j] = value1 > value2 ? value1 : value2;
		}
	}
}

System.out.println(Arrays.deepToString(max)); // 打印最大价值数组
System.out.println("MaxValue = " + max[number][bag]); // 打印最大价值

结果输出：

[[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], 
[0, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4], 
[0, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5], 
[0, 4, 4, 7, 7, 8, 8, 8, 8, 8, 8, 8, 8], 
[0, 4, 4, 7, 10, 10, 13, 13, 14, 14, 14, 14, 14], 
[0, 4, 4, 7, 10, 12, 13, 15, 18, 18, 21, 21, 22], 
[0, 4, 4, 7, 10, 12, 13, 15, 18, 18, 21, 21, 22]]
MaxValue = 22

---

在上述结果基础上，如果需要知道最大价值情况下，都装入了哪些商品，就需要进行回溯。

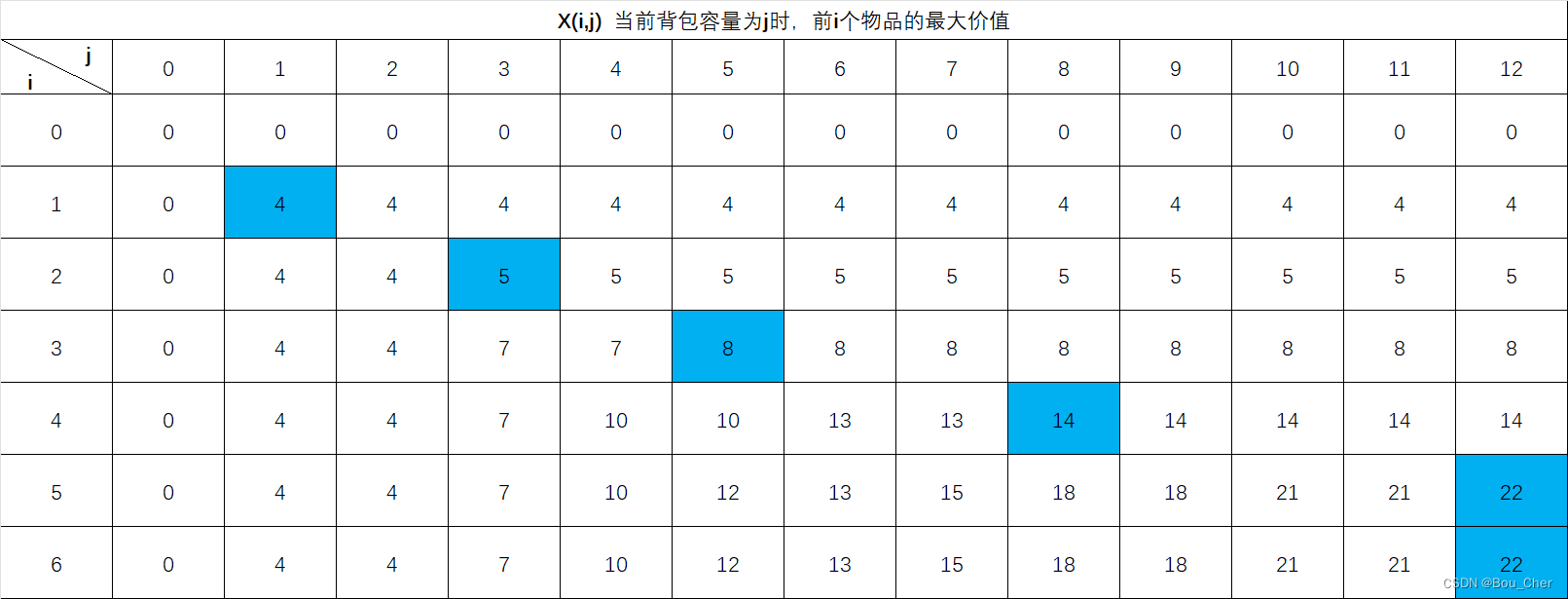
已知X[6][12] 为最大价值，首先判断它有没有装入背包，即X[6][12] = X[6-1][12] 是否生效，若相等，则未装入，继续以X[6-1][12] 作为最大价值进行判断。

X[5][12] 同理与X[5-1][12] 比较，发现不相等，通过公式22 = X[5-1][j-W(5)] + V[5] = X[4][12-4] + 8 = X[4][8] + 8 ，即X[4][8] = 22-8 = 14，反算后值也相等，则第5个物品装入了背包。

以此类推，公式为：

1. 未装入背包：
   X[i][j] = X[i-1][j]，则当前物品未装入背包。

2. 转入背包：
   X[i-1][j-W(i)] = X[i][j] - V[i]，则当前物品装入背包。

---

代码实现：

List list = new ArrayList<>(); // 装入物品编号

// 回溯查找装入物品编号
findNo(number, bag);
Collections.sort(list); // 按照物品编号排序
System.out.println(list.toString());

void findNo(int i, int j) {
	if (i > 0) {
		// 判断是否装入背包
		if (max[i][j] == max[i - 1][j]) {
			// 与上一物品最大价值相等，当前物品未装入
			findNo(i - 1, j);
		} else if (j - weight[i-1] >= 0 && (max[i - 1][j - weight[i-1]] == max[i][j] - value[i-1])) {  
			// 与上一物品最大价值不相等且反算成功，当前物品装入，继续递归
			list.add(i);
			findNo(i - 1, j - weight[i-1]);
		}
	}
}

结果输出：

[1, 2, 3, 4, 5]