A Simple Framework for Contrastive Learning of Visual Representations阅读笔记

news2024/11/18 7:38:27

在这里插入图片描述
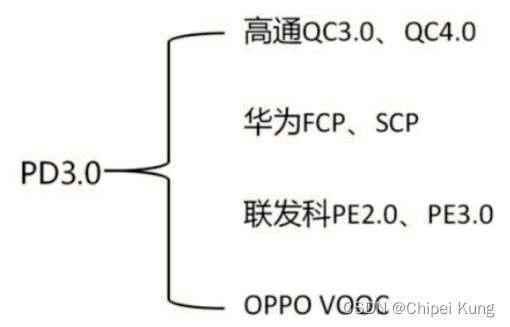
论文地址：https://arxiv.org/pdf/2002.05709.pdf

目前流行的无监督学范式。通过训练，使模型拥有比较的能力。即，模型能够区别两个数据（instance）是否是相同的。这在深度聚类领域受到广泛的关注。（在有监督中的 few-shot, 使用一些类让模型学会比较，再用一些新类去测试模型的比较能力）

我们分几个模块了解对比学习。

数据增强

对比学习主要是通过拉进正例对之间特征表示的相似度；以及拉远负例对之间特征表示的相似度。
从而使模型具有对比的能力。因为是无监督学习，我们的数据没有标签。我们构建正例对的方法就是通过数据增强（基本不改变数据的语义信息）。
数据增强的方法有很多种：
图片数据增强
文本数据增强
语音数据增强
图数据增强

正负例对的构建

原数据： $x_1, x_2, x_3)$ ;
增强数据a： $x_1^a, x_2^a, x_3^a)$ ;
增强数据b： $x_1^b, x_2^b, x_3^b)$ ;

Aug_data{a & b}	$x_1^b$	$x_2^b$	$x_3^b$
$x_1^a$	$\color{red}(x_1^a, x_1^b)$	$x_1^a, x_2^b)$	$x_1^a, x_3^b)$
$x_2^a$	$x_2^a, x_1^b)$	$\color{red}(x_2^a, x_2^b)$	$x_2^a, x_3^b)$
$x_3^a$	$x_3^a, x_1^b)$	$x_3^a, x_2^b)$	$\color{red}(x_3^a, x_3^b)$

构成的正例对：红色；
构成的负例对：黑色。

上面说的只是原始的对比对的构造方式。现在还有根据语义信息进行去除假负例对。
假负例对: $x_1, x_2$ 属于一个簇类， $x_1^a, x_2^b)$ 却属于负例对，实际上应该属于正例对，且他们的特征表示的相似度应该很大。

编码器 $\Phi(\cdot)$

将图片，文本，语音，图等进行编码。得到特征矩阵 $H$ 。
对于一个原数据： $X = \{ x_i \}_{i=0}^M$ , 我们得到其相应的增数据： $X^a = \{ x_i^a \}_{i=0}^M$ , $X^b = \{ x_i^b \}_{i=0}^M$ 。 $M$ 是batch size的大小。
然后经过编码得到特征矩阵： $H^a = \Phi(X^a), H^b = \Phi(X^b)$ ，其中， $H^a, H^b \in \mathbb{R}^{M \times hidden\_size}$ 。

Project head $f(\cdot)$

一般使用一个两层的线性MLP或者三层的非线性MLP。将得到的Feature Matrix映射到一个字空间（subspace）。一般都是将其映射为128维。
对于得到的特征矩阵： $H^a, H^b$ 。我们经过 $f(\cdot)$ 得到映射的子空间： $Z^a = f(H^a), Z^b = f(H^b)$ ，其中， $Z^a, Z^b \in \mathbb{R}^{M \times 128}$ 。

最小化对比损失

得到子空间表示后，在使用对比损失函数，最小化损失函数。

$\mathcal{l}^a_i = -\log \frac{\exp(s(z_i^a, z_i^b)/\tau)}{\sum_{j=1}^{M} [\exp(s(z_i^a, z_j^a)/\tau) + \exp(s(z_i^a, z_j^b)/\tau) ]} \\ \mathcal{l}^b_i = -\log \frac{\exp(s(z_i^b, z_i^a)/\tau)}{\sum_{j=1}^{M} [\exp(s(z_i^b, z_j^a)/\tau) + \exp(s(z_i^b, z_j^b)/\tau) ]} \\ \mathcal{L} = \frac{1}{2M} \sum_{i=1}^{M} (\mathcal{l}^a_i + \mathcal{l}^b_i)$
其中， $\tau$ 是温度参数， $M$ 是batch size的大小， $s(\cdot)$ 是相似性度量，具体表达为： $s(z_i, z_j) = z_i^Tz_j / ||z_i||_2 \cdot ||z_j||_2$ 。