目录

3.4更强的安全观念

3.4.1 多明文加密安全

多消息窃听实验

DEFINITION 3.18 多明文加密下的不可区分性

PROPOSITION 3.19 定义3.18强于定义3.8的事实证明

PROPOSITION 3.19 的证明

概率加密的必要性

THEOREM 3.20

---

3.4更强的安全观念

到目前为止，我们一直在考虑一个相对较弱的安全定义，即对手只被动地窃听诚实当事人之间发送的单个密文。这里我们考虑更强的安全概念。

---

3.4.1 多明文加密安全

多消息窃听实验

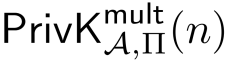
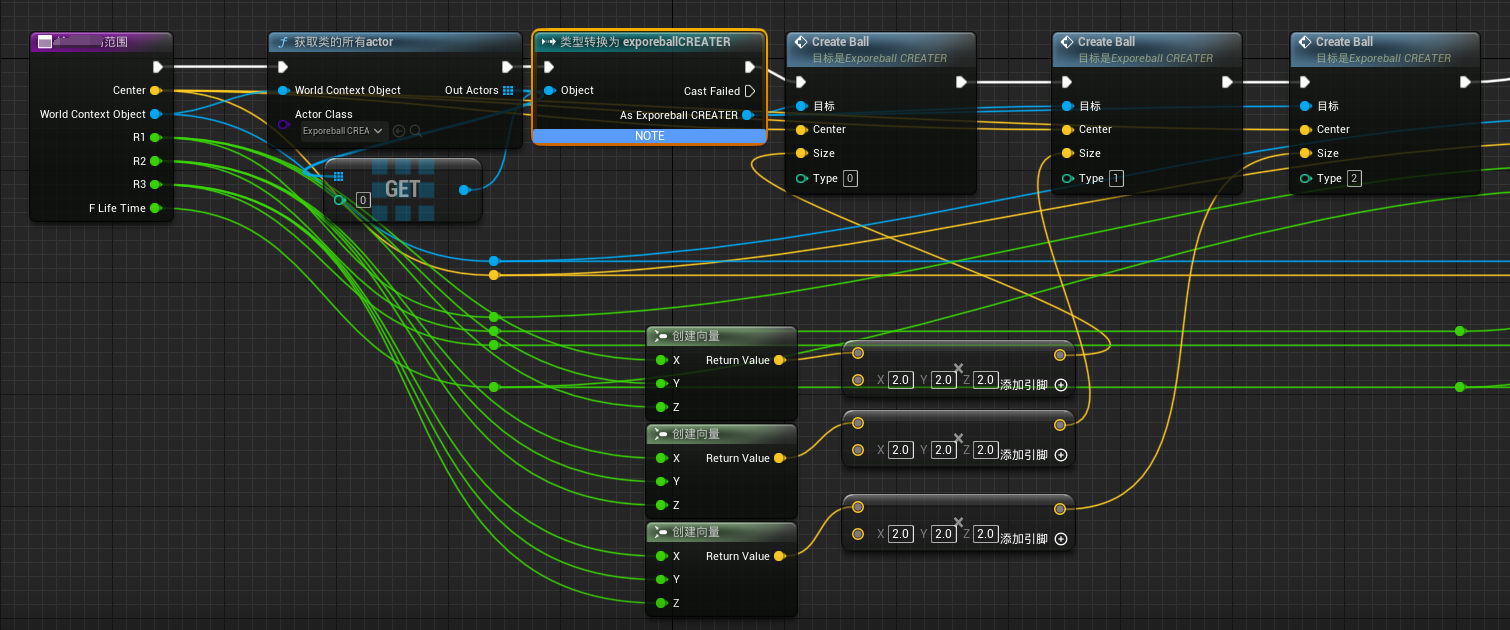
1. 对手A被给予输入1^n，并输出一对等长度的消息向量M0和M1。其中M0为

 

M1为

 

对于任何i，下式成立

 

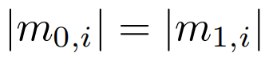
2. 通过运行Gen(1^n)产生密钥k，随机均匀选择一个比特b∈{0,1}。对于所有的i

 

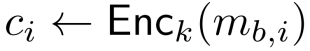
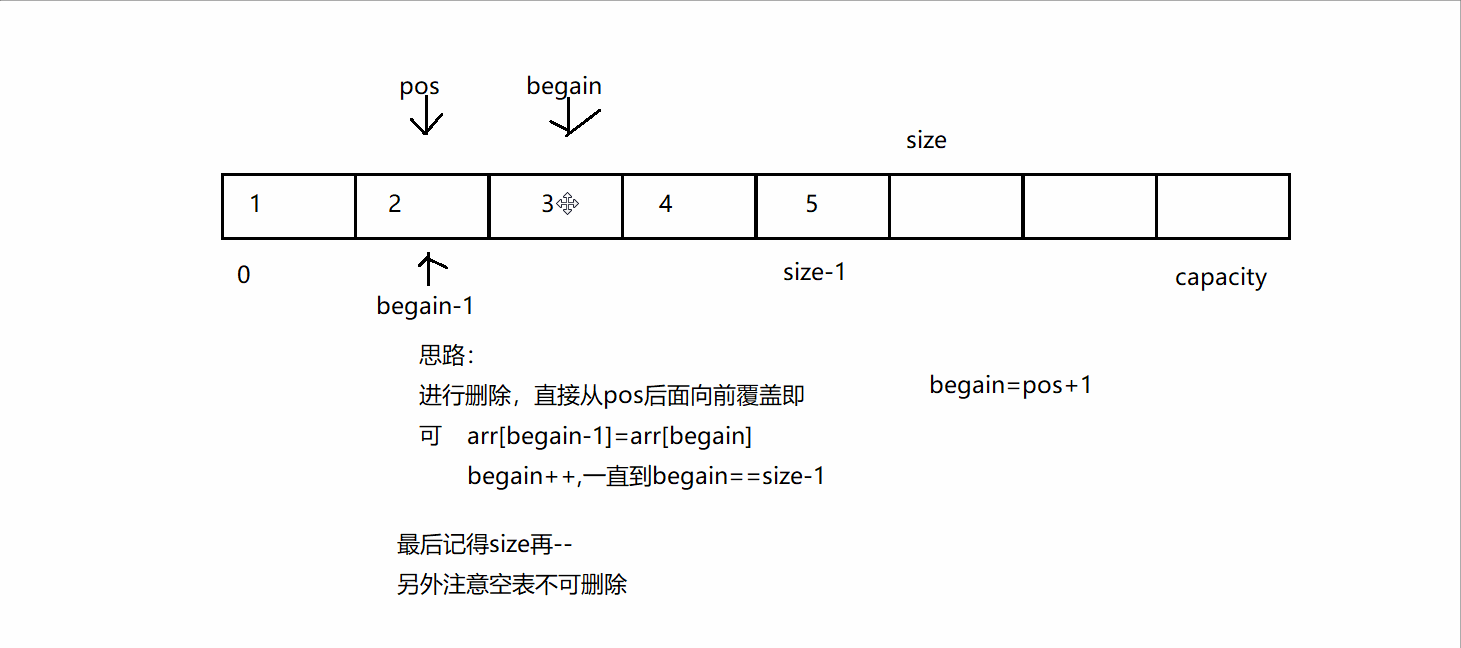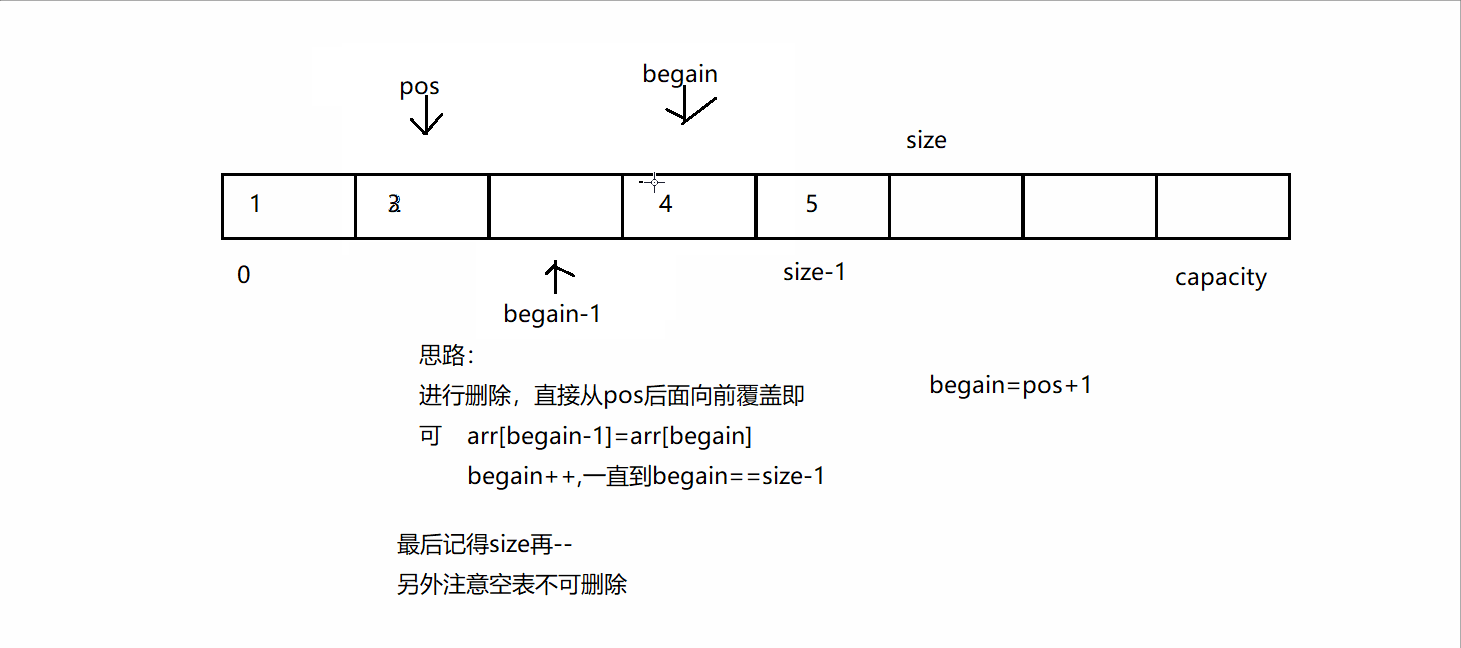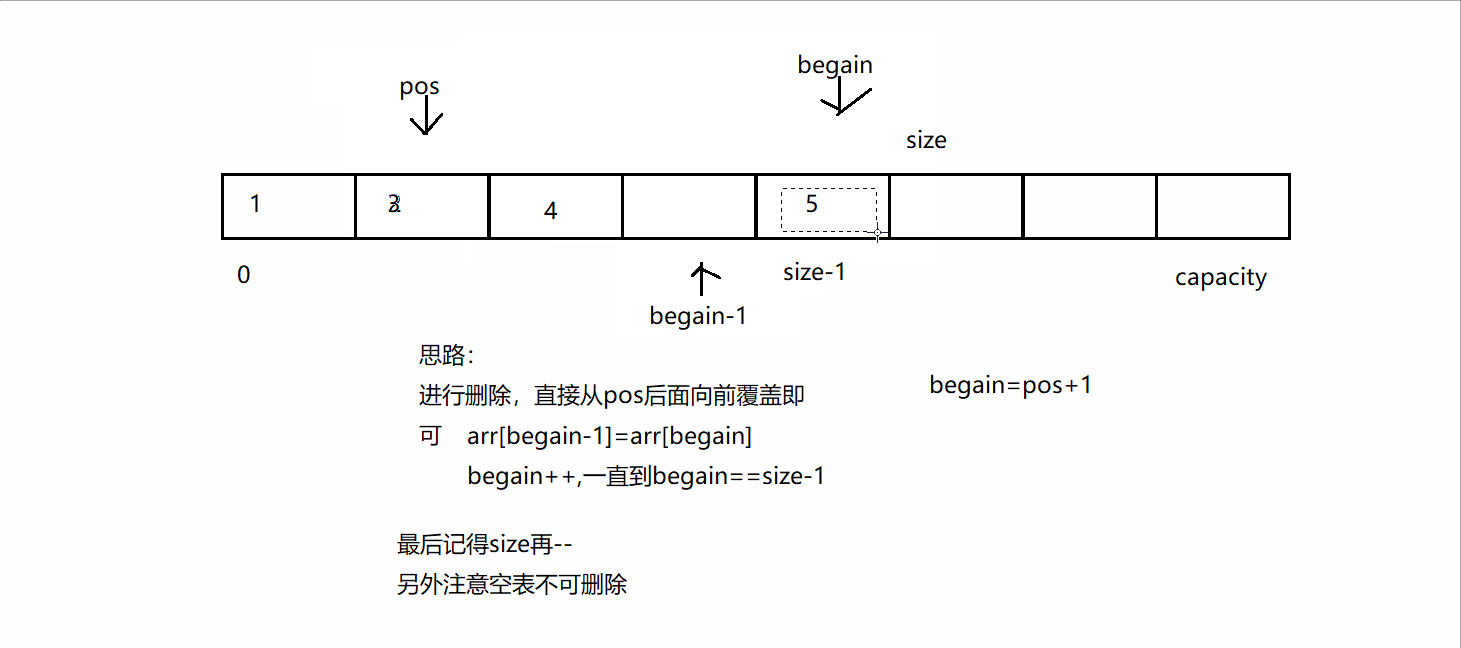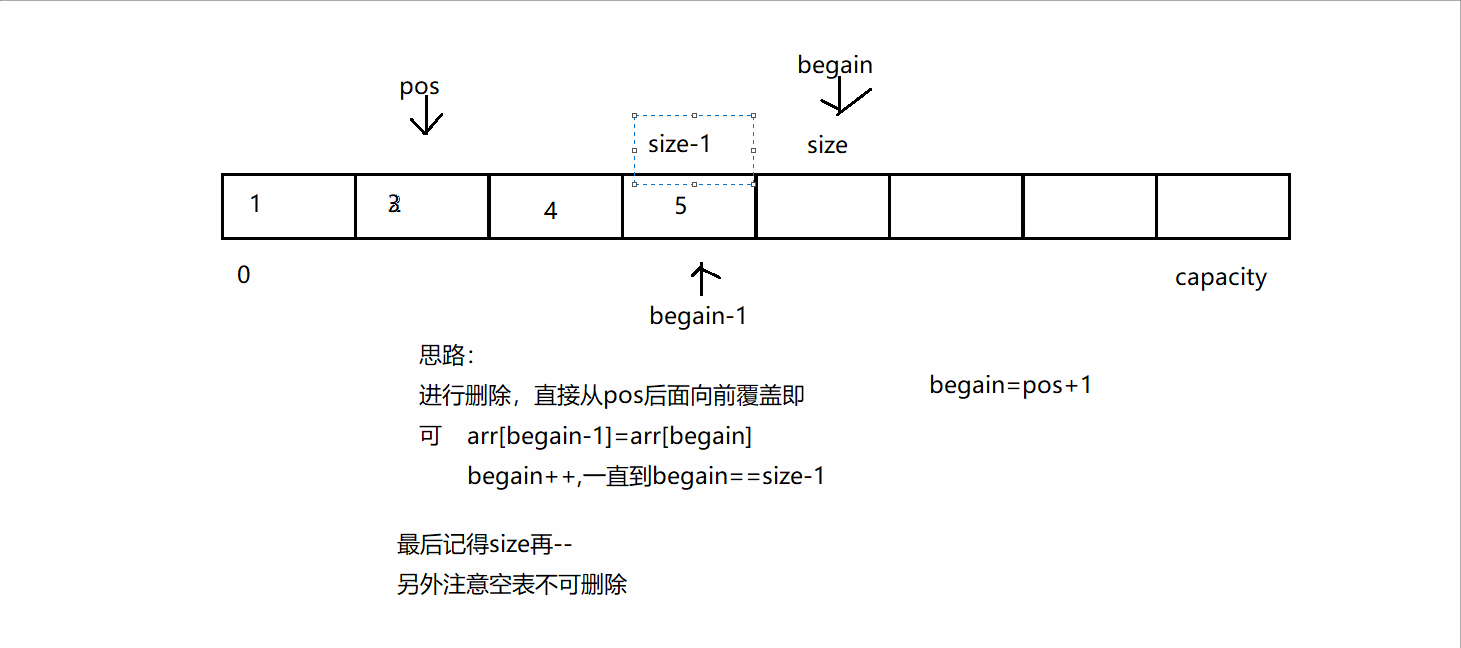
将消息列表C = (c1, . . . , ct)返回给敌手A

3. A输出一个比特b’

4. 如果b’ = b，则该实验的输出为1，否则为0

---

DEFINITION 3.18 多明文加密下的不可区分性

私钥加密方案Π=（Gen，Enc，Dec）如果对于所有的PPT敌手A，都存在可忽略函数negl使得

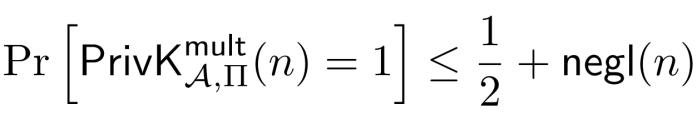
那么完美就说该方案具有多明文加密下的不可区分性

---

PROPOSITION 3.19 定义3.18强于定义3.8的事实证明

关于定义3.8见文章现代密码学导论-10-EAV安全_南鸢北折的博客-CSDN博客

存在某个私钥加密方案满足单明文加密下的不可区分性

但不满足多明文加密下的不可区分性

---

PROPOSITION 3.19 的证明

我们已经在之前提到过，一次性密码本方案是完善保密的，因此其满足单明文加密下的不可区分性。但是其不满足多明文加密下的不可区分性，因为将两次截获的密文进行异或就可以得到对应明文的异或，这样相当于在密文中获取了有关明文的信息，显然不再满足不可区分性了。详见

现代密码学导论-5-一次性密码本_南鸢北折的博客-CSDN博客

上文中的：为什么要“一次性”？

---

概率加密的必要性

我们根据定义3.18分析敌手A的攻击方式

假设敌手在多明文区分实验中采取这样的策略：

敌手A输出的两个消息向量分别为

 

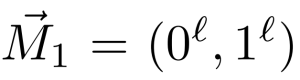
显然，第一个消息向量包含两次相同的消息，而第二个消息向量则包含两个不同的消息。

假设C = (c1, c2)是敌手A收到的挑战密文

如果为c1 = c2，则A输出b’= 0；否则，A输出b’ = 1

我们现在分析b’ = b的概率，即敌手A成功的概率。如果加密算法是确定性的，那么当b=0时，M0中两个相同的分量会被加密为相同的密文，即c1 = c2，此时敌手A输出b’= 0，此时b’ = b；当b=1时，M1中两个不同的分量会被加密为不同的密文，即c1≠c2，此时敌手A输出b’= 1，此时b’ = b。

综上所述，如果A使用上述策略，那么实验输出1的概率为1，所以如果加密算法是确定性的，该方案就不具备多明文下的不可区分性。

以上情况表明，使用任何确定性的加密方案都不可能实现定义3.18。

---

THEOREM 3.20

如果Π是一种加密方案，其中Enc是密钥和消息的确定性函数，那么Π不满足多明文加密下的不可区分性。

注意：定理3.20仅指满足定义3.7语法的加密方案。我们将在第3.6.2节中看到，如果一个加密方案是有状态的（定义3.7没有涵盖的内容），那么即使Enc是确定性的，也可以安全地加密多个消息。