Prim算法

题目描述：


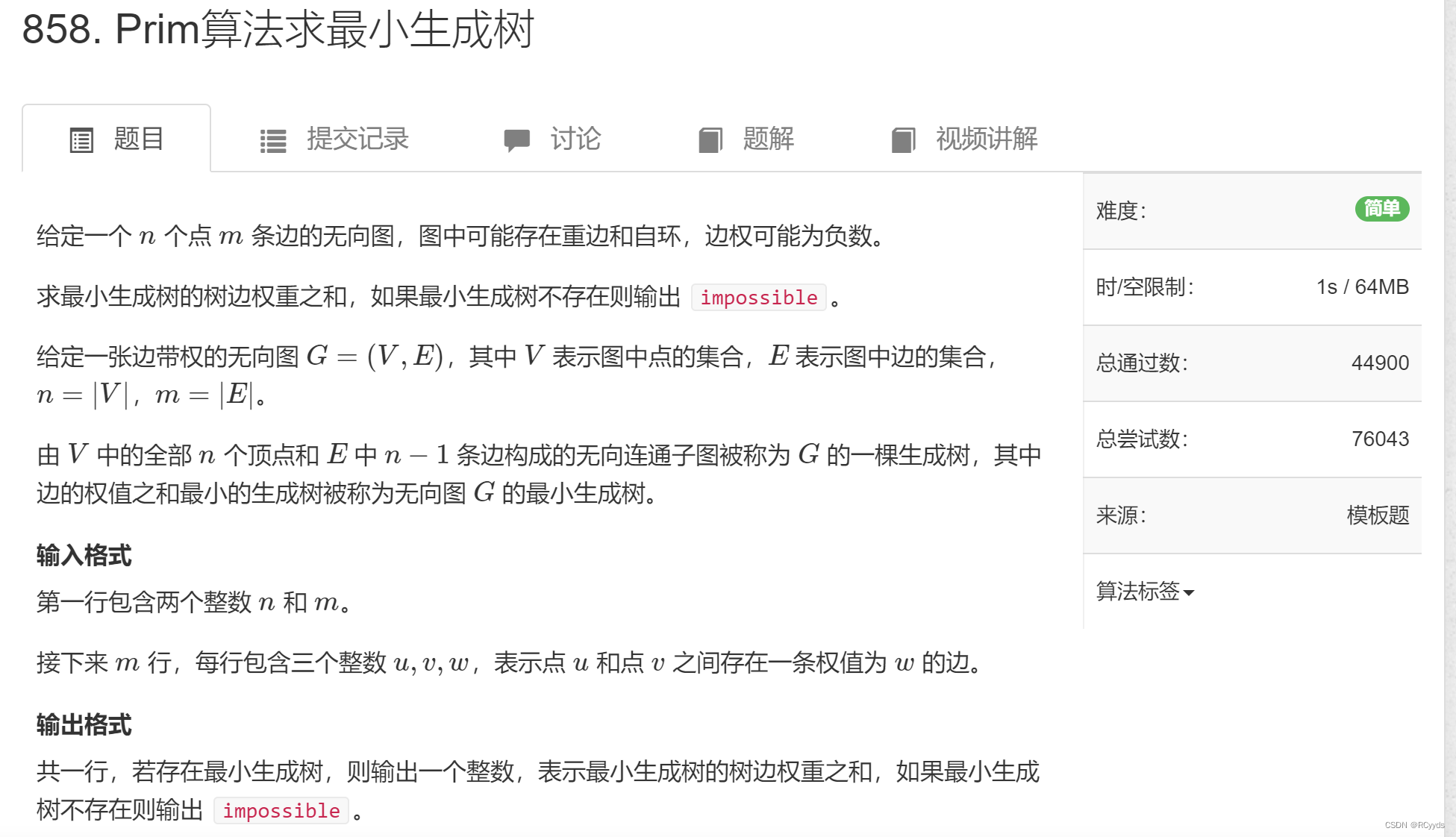
解析：
prim算法跟dijkstra的朴素解法有很多相像部分，他们都是枚举中继节点来更新下一个节点，都是选最小的dist值来更新，时间复杂度都是O(n✖n)。

不同之处在于:
dijkstra的dist[i]表示1号点到i号点的最小距离，而prim的dist[i]表示用来更新dist[i]的中继节点与i点的最小距离。

所以prim算法每次更新时都会加上dist[t]，然后通过dist[t]来更新与之相连的节点的dist值。

那么为什么这样做可以算出最小生成树呢？
因为每次求出最小的dist[t]时，就代表着求出了用来更新dist[t]的中继节点与t点之间的最小值，又由于中继节点用完了就不能用了，如此循环n次就能求出最小生成树了。

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=510,INF=0x3f3f3f3f;
int n,m,g[N][N],dist[N],st[N];
int prim()
{
	memset(dist,0x3f,sizeof(dist));
	int res=0;
	for(int i=0;i<n;i++)
	{
		int t=-1;
		for(int j=1;j<=n;j++)
		{
			if(!st[j]&&(t==-1||dist[t]>dist[j]))
			t=j;
		}
		if(i&&dist[t]==INF) return INF;
		if(i) res+=dist[t];
		for(int j=1;j<=n;j++) dist[j]=min(dist[j],g[t][j]);
		st[t]=1;
	}
	return res;
}
int main()
{
	scanf("%d%d",&n,&m);
	memset(g,0x3f,sizeof(g));
	while(m--)
	{
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		g[u][v]=g[v][u]=min(g[u][v],w);
	}
	int t=prim();
	if(t==INF) printf("impossible");
	else printf("%d",t);
	return 0;
}

Kruskal算法

题目描述：


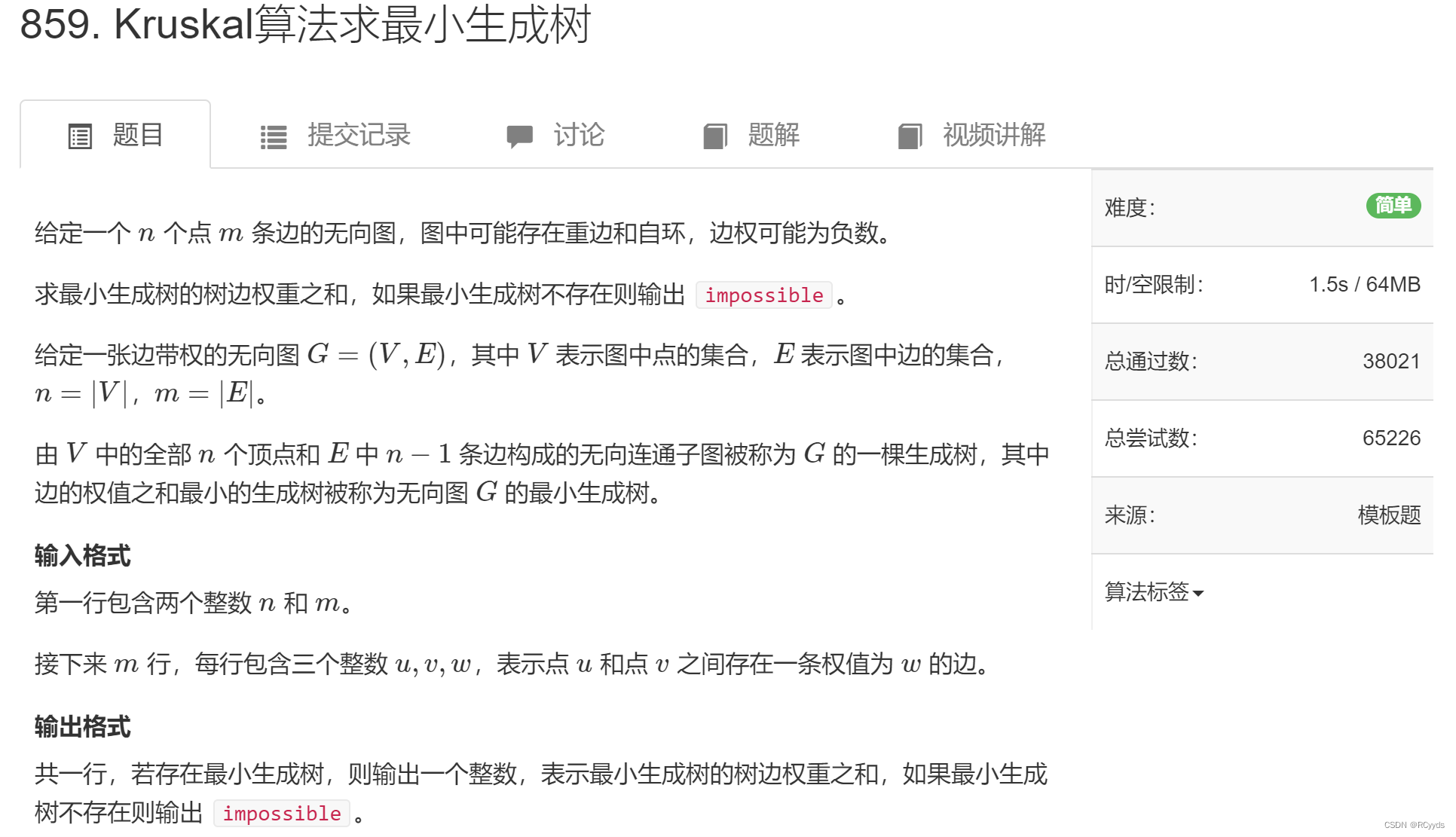
解析：
Kruskal算法跟dijkstra的堆优化版有点类似，都是枚举边，但写法上有很大不同，dijkstra是用单链表来存边的，Kruskal则是用结构体来存，而且枚举边的方法也有很大的不同，Kruskal单纯地从小到大枚举边，而堆优化版的dijkstra则是用到了优先队列来存边和点，然后从中选最小的dist值，情况更复杂；

当然，由于题目性质不同，这两个解法肯定不同，接下来就说Kruskal的具体解法：
先是用结构体存边，再对边进行从小到大的排序，然后枚举边，判断边上的两个节点是否在同一个连通块里，不在就把他们连起来，res加上边的值，cnt++(res用来统计权值之和，cnt用来统计连通块中边的数目)，如此循环m次，判断cnt是否等于n-1，是则能求出最小生成树，否则就不存在。

那么为什么这种解法可以求出最小生成树呢？
因为每次循环，如果两个点不在同一个连通块里，就能确定两个点之间的最小值，如此循环m次，如果存在最小生成树的话，就一定能求出能将所有点相连的具有n个点，n-1条边的生成树，而且是最小的。

代码：

#include<bits/stdc++.h>
using namespace std;
const int M=2e5+10,N=1e5+10,INF=0x3f3f3f3f;
int n,m,p[N];
struct node{
	int a,b,w;
}edges[M];
int find(int x){
	if(p[x]!=x) p[x]=find(p[x]);
	return p[x];
}
bool cmp(node x,node y)
{
	return x.w<y.w;
}
int kruskal()
{
	sort(edges,edges+m,cmp);
	
	for(int i=1;i<=n;i++) p[i]=i;
	
	int res=0,cnt=0;
	for(int i=0;i<m;i++)
	{
		int a=edges[i].a,b=edges[i].b,w=edges[i].w;
		a=find(a),b=find(b);
		if(a!=b)
		{
			p[a]=b;
			res+=w;
			cnt++; 
		}
	}
	if(cnt==n-1) return res;
	else return INF;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=0;i<m;i++)
	{
		int a,b,w;
		scanf("%d%d%d",&a,&b,&w);
		edges[i]={a,b,w};
	}
	int t=kruskal();
	if(t==INF) printf("impossible");
	else printf("%d",t);
}