本文仅供学习使用
本文参考:
《机构运动微分几何学分析与综合》-王德伦、汪伟
《微分几何》吴大任
Ch02-3 平面机构离散运动鞍点综合
- 2.4 鞍滑点
- 2.4.1 鞍线与二副连架杆P-R
- 2.4.2 鞍线误差
- 2.4.3 三位置鞍线
- 2.4.4 四位置鞍线
2.4 鞍滑点
在平面机构运动综合时,往往期望用二副杆P-R作为连架杆,而二副杆P-R对应的约束曲线为直线。寻求平面运动刚体上点,使其离散轨迹与直线的差异尽可能小,以便综合出连架杆P-R,是平面离散运动几何学研究的另一重要内容。在三到四个离散位置时,经典理论已经表明运动刚体上有滑点圆和滑点存在,而对于多位置运动刚体上点及其离散轨迹与直线比较,尚在讨论之中。本节以最大误差最小准则评价离散曲线逼近直线的性质,进而讨论运动刚体上点的离散轨迹与直线的差异,建立鞍点规划模型,寻求离散运动刚体上的鞍滑点。
2.4.1 鞍线与二副连架杆P-R
对于刚体运动平面上一点在固定坐标系
{
O
f
;
i
⃗
f
,
j
⃗
f
}
\{{{O}_{f}};{{{\vec{i}}}_{f}},{{{\vec{j}}}_{f}}\}
{Of;if,jf}中的离散轨迹点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}评价直线与
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}的接近程度,需用直线拟合,可依据直线的曲率为零的不变量性质,不涉及直线位置,采用类似2.3节鞍圆拟合的定义和定理,有∶
定义2.3 依据被拟合离散点集 { R P ( i ) } \{R_{P}^{(i)}\} {RP(i)}的性质并按最大法向拟合误差为最小原则得到唯一的拟合直线,称为鞍点意义下的自适应拟合直线,简称鞍线,对应的最大法向拟合误差称为鞍线误差。
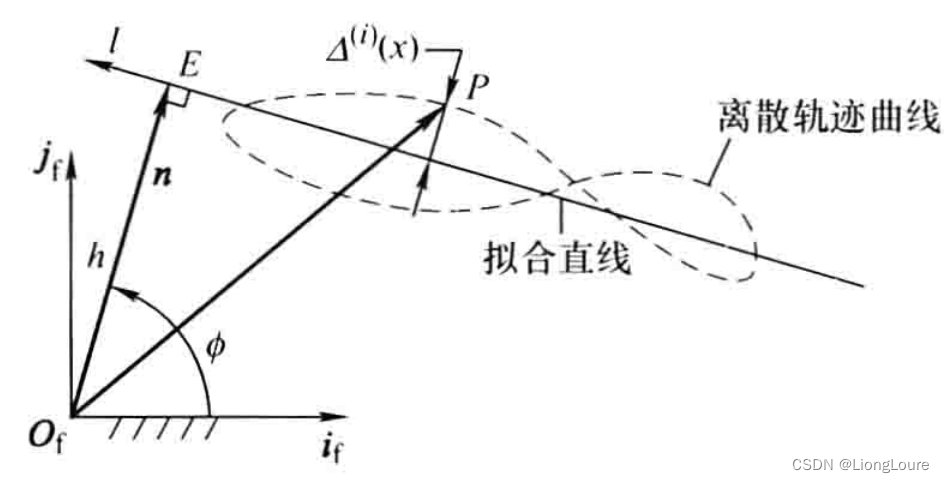
运动刚体
Σ
∗
\Sigma *
Σ∗上的点
P
P
P在固定坐标系
{
O
f
;
i
⃗
f
,
j
⃗
f
}
\{{{O}_{f}};{{{\vec{i}}}_{f}},{{{\vec{j}}}_{f}}\}
{Of;if,jf}中的离散轨迹点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)},将其矢量方程按最大拟合误差最小原则用直线进行自适应拟合,自固定坐标系坐标原点
O
f
{{O}_{f}}
Of作直线的垂线,取垂足
E
E
E为参考点,其矢径为
R
⃗
E
=
(
h
cos
ϕ
,
h
sin
ϕ
)
T
{\vec R_E} = {(h\cos \phi ,h\sin \phi )^T}
RE=(hcosϕ,hsinϕ)T,其中
h
h
h与
ϕ
\phi
ϕ分别为垂线的长度以及方向角,而直线的单位方向矢量为
l
⃗
=
(
−
sin
ϕ
,
cos
ϕ
)
T
\vec l = {( - \sin \phi ,\cos \phi )^T}
l=(−sinϕ,cosϕ)T,如上图所示。
建立鞍线拟合的误差模型为∶
{
Δ
p
r
=
min
x
max
1
≤
i
≤
n
{
Δ
(
i
)
(
x
)
}
=
min
x
max
1
≤
i
≤
n
{
∣
x
P
(
i
)
cos
ϕ
+
y
P
(
i
)
sin
ϕ
−
h
∣
}
s
.
t
.
h
∈
[
0
,
+
∞
)
,
ϕ
∈
[
0
,
2
π
)
x
=
(
h
,
ϕ
)
T
\left\{ \begin{matrix} {{\Delta }_{pr}}=\underset{x}{\mathop{\min }}\,\underset{1\le i\le n}{\mathop{\max }}\,\{{{\Delta }^{(i)}}(x)\}=\underset{x}{\mathop{\min }}\,\underset{1\le i\le n}{\mathop{\max }}\,\{\left| x_{P}^{(i)}\cos \phi +y_{P}^{(i)}\sin \phi -h \right|\} \\ \begin{matrix} s.t. & h\in [0,+\infty ),\phi \in [0,2\pi ) \\ \end{matrix} \\ x={{(h,\phi )}^{T}} \\ \end{matrix} \right.
⎩⎪⎨⎪⎧Δpr=xmin1≤i≤nmax{Δ(i)(x)}=xmin1≤i≤nmax{∣∣∣xP(i)cosϕ+yP(i)sinϕ−h∣∣∣}s.t.h∈[0,+∞),ϕ∈[0,2π)x=(h,ϕ)T
Δ ( i ) ( x ) = R ⃗ P ( i ) ⋅ R ⃗ E ∣ R ⃗ E ∣ − ∣ R ⃗ E ∣ {{\Delta }^{(i)}}(x)=\vec{R}_{P}^{(i)}\cdot \frac{{{{\vec{R}}}_{E}}}{\left| {{{\vec{R}}}_{E}} \right|}-\left| {{{\vec{R}}}_{E}} \right| Δ(i)(x)=RP(i)⋅∣RE∣RE−∣∣∣RE∣∣∣
式中,
n
n
n为已知离散点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}中离散点的个数,
{
Δ
(
i
)
(
x
)
}
=
{
∣
x
P
(
i
)
cos
ϕ
+
y
P
(
i
)
sin
ϕ
−
h
∣
}
\{{{\Delta }^{(i)}}(x)\}=\{\left| x_{P}^{(i)}\cos \phi +y_{P}^{(i)}\sin \phi -h \right|\}
{Δ(i)(x)}={∣∣∣xP(i)cosϕ+yP(i)sinϕ−h∣∣∣}为
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}中的点与浮动拟合直线的误差集合,
Δ
p
r
{{\Delta }_{pr}}
Δpr为目标函数的输出值,即鞍线误差。优化变量
x
=
(
h
,
ϕ
)
T
x={{(h,\phi )}^{T}}
x=(h,ϕ)T为刚体平面上任意直线的参数。该优化模型同样是一个离散函数鞍点规划问题,并直接应用MATLAB软件优化工具箱中的fminimax函数进行求解,其具体参数设置将在后续算例中进行介绍。同鞍圆一样,为简便得到初始值,采用最小二乘意义下直线拟合离散点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)},计算出初始值。对于给定的离散点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)},用直线
R
⃗
L
=
R
⃗
E
+
λ
l
⃗
{{{\vec{R}}}_{L}}={{{\vec{R}}}_{E}}+\lambda \vec{l}
RL=RE+λl去逼近时,今残差为:
e
i
=
∣
x
P
(
i
)
cos
ϕ
+
y
P
(
i
)
sin
ϕ
−
h
∣
{{e}_{i}}=\left| x_{P}^{(i)}\cos \phi +y_{P}^{(i)}\sin \phi -h \right|
ei=∣∣∣xP(i)cosϕ+yP(i)sinϕ−h∣∣∣
则可得残差的平方和为∶
F
=
∑
i
=
1
n
e
i
2
=
∑
i
=
1
n
(
x
P
(
i
)
cos
ϕ
+
y
P
(
i
)
sin
ϕ
−
h
)
2
F=\sum\limits_{i=1}^{n}{{{e}_{i}}^{2}}=\sum\limits_{i=1}^{n}{{{(x_{P}^{(i)}\cos \phi +y_{P}^{(i)}\sin \phi -h)}^{2}}}
F=i=1∑nei2=i=1∑n(xP(i)cosϕ+yP(i)sinϕ−h)2
将上式分别对参数
ϕ
\phi
ϕ和
h
h
h求导并令其为零,可得∶
{
∂
F
∂
ϕ
=
2
∑
i
=
1
n
(
x
P
(
i
)
cos
ϕ
+
y
P
(
i
)
sin
ϕ
−
h
)
⋅
(
−
x
P
(
i
)
sin
ϕ
+
y
P
(
i
)
cos
ϕ
)
=
0
∂
F
∂
h
=
−
2
∑
i
=
1
n
(
x
P
(
i
)
cos
ϕ
+
y
P
(
i
)
sin
ϕ
−
h
)
=
0
\left\{ \begin{matrix} \frac{\partial F}{\partial \phi }=2\sum\limits_{i=1}^{n}{(x_{P}^{(i)}\cos \phi +y_{P}^{(i)}\sin \phi -h)}\cdot (-x_{P}^{(i)}\sin \phi +y_{P}^{(i)}\cos \phi )=0 \\ \frac{\partial F}{\partial h}=-2\sum\limits_{i=1}^{n}{(x_{P}^{(i)}\cos \phi +y_{P}^{(i)}\sin \phi -h)}=0 \\ \end{matrix} \right.
⎩⎪⎨⎪⎧∂ϕ∂F=2i=1∑n(xP(i)cosϕ+yP(i)sinϕ−h)⋅(−xP(i)sinϕ+yP(i)cosϕ)=0∂h∂F=−2i=1∑n(xP(i)cosϕ+yP(i)sinϕ−h)=0
由上式可得到最小二乘意义下的直线的参数
ϕ
\phi
ϕ和
h
h
h∶
{
cot
ϕ
=
−
n
∑
i
=
1
n
x
P
(
i
)
y
P
(
i
)
−
∑
i
=
1
n
x
P
(
i
)
∑
i
=
1
n
y
P
(
i
)
n
∑
i
=
1
n
(
x
P
(
i
)
)
2
−
(
∑
i
=
1
n
x
P
(
i
)
)
2
h
=
sin
ϕ
⋅
n
∑
i
=
1
n
(
x
P
(
i
)
)
2
∑
i
=
1
n
y
P
(
i
)
−
∑
i
=
1
n
x
P
(
i
)
∑
i
=
1
n
x
P
(
i
)
y
P
(
i
)
n
∑
i
=
1
n
(
x
P
(
i
)
)
2
−
(
∑
i
=
1
n
x
P
(
i
)
)
2
\left\{ \begin{matrix} \cot \phi =-\frac{n\sum\limits_{i=1}^{n}{x_{P}^{(i)}y_{P}^{(i)}}-\sum\limits_{i=1}^{n}{x_{P}^{(i)}}\sum\limits_{i=1}^{n}{y_{P}^{(i)}}}{n\sum\limits_{i=1}^{n}{{{(x_{P}^{(i)})}^{2}}}-{{(\sum\limits_{i=1}^{n}{x_{P}^{(i)}})}^{2}}} \\ h=\sin \phi \cdot \frac{n\sum\limits_{i=1}^{n}{{{(x_{P}^{(i)})}^{2}}}\sum\limits_{i=1}^{n}{y_{P}^{(i)}}-\sum\limits_{i=1}^{n}{x_{P}^{(i)}}\sum\limits_{i=1}^{n}{x_{P}^{(i)}y_{P}^{(i)}}}{n\sum\limits_{i=1}^{n}{{{(x_{P}^{(i)})}^{2}}}-{{(\sum\limits_{i=1}^{n}{x_{P}^{(i)}})}^{2}}} \\ \end{matrix} \right.
⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧cotϕ=−ni=1∑n(xP(i))2−(i=1∑nxP(i))2ni=1∑nxP(i)yP(i)−i=1∑nxP(i)i=1∑nyP(i)h=sinϕ⋅ni=1∑n(xP(i))2−(i=1∑nxP(i))2ni=1∑n(xP(i))2i=1∑nyP(i)−i=1∑nxP(i)i=1∑nxP(i)yP(i)
对于给定离散运动
(
x
O
m
f
(
i
)
,
y
O
m
f
(
i
)
,
γ
(
i
)
)
(x_{Omf}^{(i)},y_{Omf}^{(i)},{{\gamma }^{(i)}})
(xOmf(i),yOmf(i),γ(i))的刚体上任意点
P
P
P,其在固定坐标系
{
O
f
;
i
⃗
f
,
j
⃗
f
}
\{{{O}_{f}};{{{\vec{i}}}_{f}},{{{\vec{j}}}_{f}}\}
{Of;if,jf}中的离散轨迹可计算得出,根据鞍线的定义以及误差模型,直接采用MATLAB软件优化工具箱中的fminimax函数,采用类似鞍圆拟合的参数设置进行求解,同样可以将基于离散点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}的鞍线拟合编制成子函数(AprF),该子函数的输入为离散点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}中各点的坐标,输出为鞍线的直线参数
(
h
,
ϕ
)
(h,\phi )
(h,ϕ)以及鞍线误差
Δ
p
r
{{\Delta }_{pr}}
Δpr,形成鞍线子程序AprF。
2.4.2 鞍线误差
为讨论平面曲线鞍线拟合的误差性质,假定运动平面上点在固定坐标系中的轨迹
Γ
P
{{\Gamma }_{P}}
ΓP,为连续曲线,在定义2.3中按最大法向拟合误差最小为原则确定了唯一的鞍线
L
L
L,其拟合误差对于曲线
Γ
P
{{\Gamma }_{P}}
ΓP上所有点而言是最大误差(全局最大值),而对于所有拟合直线参数
h
∈
(
0
,
+
∞
)
,
ϕ
∈
[
0
,
2
π
)
h\in (0,+\infty ),\phi \in [0,2\pi )
h∈(0,+∞),ϕ∈[0,2π)而言,该最大误差值又是最小的。如上图所示,鞍线
L
L
L的矢量方程为
R
⃗
L
=
R
⃗
E
+
λ
l
⃗
{{{\vec{R}}}_{L}}={{{\vec{R}}}_{E}}+\lambda \vec{l}
RL=RE+λl,那么,鞍线
L
L
L的单位法矢
n
⃗
{\vec{n}}
n与其单位矢量
l
⃗
{\vec{l}}
l正交,曲线
Γ
P
{{\Gamma }_{P}}
ΓP与鞍线的法向距离为误差
Δ
\Delta
Δ,曲线
Γ
P
{{\Gamma }_{P}}
ΓP上
P
P
P点的矢径
R
⃗
P
{{{\vec{R}}}_{P}}
RP,可由鞍线的矢量方程以及法向误差
Δ
\Delta
Δ表示为∶
R
⃗
P
=
R
⃗
E
+
λ
l
⃗
+
Δ
n
⃗
{{{\vec{R}}}_{P}}={{{\vec{R}}}_{E}}+\lambda \vec{l}+\Delta \vec{n}
RP=RE+λl+Δn
由上式得到鞍线
L
L
L与曲线
Γ
P
{{\Gamma }_{P}}
ΓP之间的法向误差为∶
Δ
=
(
R
⃗
P
−
R
⃗
E
)
⋅
n
⃗
\Delta =({{{\vec{R}}}_{P}}-{{{\vec{R}}}_{E}})\cdot \vec{n}
Δ=(RP−RE)⋅n
对于鞍线
L
L
L,参考点
R
⃗
E
{{{\vec{R}}}_{E}}
RE和法向单位矢量
n
⃗
{\vec{n}}
n均为常矢量,将误差表达式对曲线
Γ
P
{{\Gamma }_{P}}
ΓP的弧长
s
s
s求导,有∶
d
Δ
d
s
=
d
R
⃗
P
d
s
⋅
n
⃗
\frac{d\Delta }{ds}=\frac{d{{{\vec{R}}}_{P}}}{ds}\cdot \vec{n}
dsdΔ=dsdRP⋅n
在曲线
Γ
P
{{\Gamma }_{P}}
ΓP上
P
P
P点处误差
Δ
\Delta
Δ取得极值的条件为
d
Δ
d
s
=
0
\frac{d\Delta }{ds}=0
dsdΔ=0,由上式可得∶
d
R
⃗
P
d
s
⋅
n
⃗
=
0
\frac{d{{{\vec{R}}}_{P}}}{ds}\cdot \vec{n}=0
dsdRP⋅n=0
上式说明曲线
Γ
P
{{\Gamma }_{P}}
ΓP上
P
P
P点的切线
d
R
⃗
P
d
s
\frac{d{{{\vec{R}}}_{P}}}{ds}
dsdRP与鞍线的法线
n
⃗
{\vec{n}}
n正交,此时曲线
Γ
P
{{\Gamma }_{P}}
ΓP上
P
P
P点法线与鞍线的法线重合。而曲线
Γ
P
{{\Gamma }_{P}}
ΓP上可能存在有多点处的法线与鞍线垂直,这些点的误差取得极值,但不一定是最大值,如下图所示的点
P
(
k
+
1
)
,
P
(
k
+
2
)
{{P}^{(k+1)}},{{P}^{(k+2)}}
P(k+1),P(k+2)和
P
(
k
+
3
)
{{P}^{(k+3)}}
P(k+3)
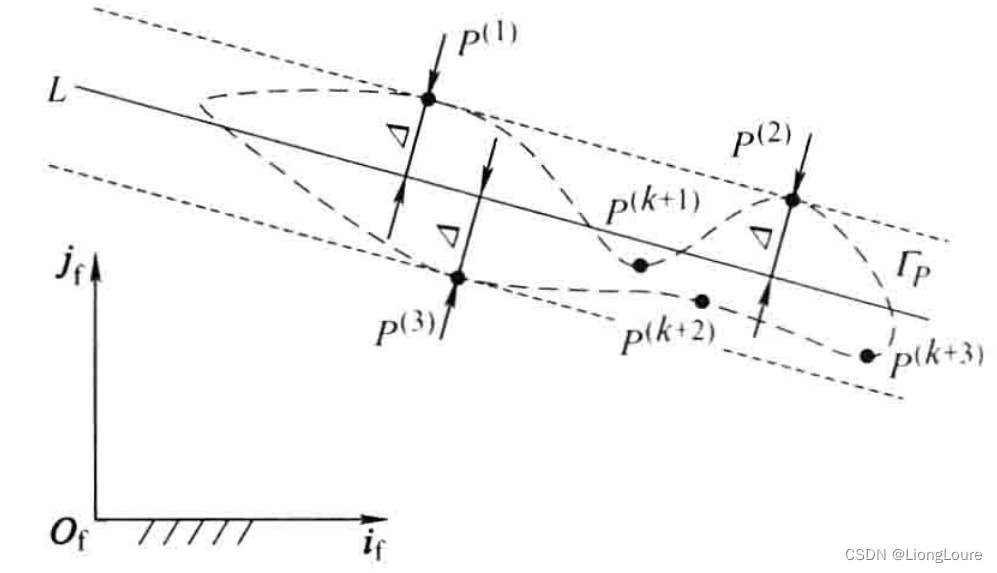
对于给定曲线
Γ
P
{{\Gamma }_{P}}
ΓP其上各点的
(
R
⃗
P
,
d
R
⃗
P
d
s
×
k
⃗
)
({{{\vec{R}}}_{P}},\frac{d{{{\vec{R}}}_{P}}}{ds}\times \vec{k})
(RP,dsdRP×k)已知,若确定其鞍线,至少需要有三个点使得上式成立。由法向误差求得其相应的法向误差并判断是否为最大值,从而解出鞍线的两个参数
(
h
,
ϕ
)
(h,\phi )
(h,ϕ)和误差
Δ
\Delta
Δ,多于三点则为冗余情况。采用两条平行直线包容被拟合曲线,上图所示两条虚线直线,依据鞍点规划模型,两平行直线与被包容曲线的三个切点即为最大误差点。鞍点规划理论已经证明至少有三个点的误差取得相等且为最大值,并分布在鞍线
L
L
L的两侧。
由此可见,以鞍点规划(最大误差最小)模型评价一条曲线与直线的近似程度由该曲线上三个特征点体现,称为鞍线拟合特征点,分布在直线两侧,并且具有相同误差值,也就是由这三个鞍线拟合特征点确定了鞍线的方向和位置。当鞍线误差趋于零时,被拟合曲线趋近于直线。其他点的误差未计入评价,但可能会影响鞍线拟合极值的选取。
当被拟合曲线为运动刚体上点的离散轨迹点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}时,连续曲线上的鞍线拟合特征点由离散点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}中产生。由于曲线不再连续,曲线上任意点与鞍线的误差
Δ
(
i
)
{{\Delta }^{(i)}}
Δ(i)表达式改写为∶
Δ
(
i
)
=
(
R
⃗
P
(
i
)
−
R
⃗
E
)
⋅
n
⃗
,
R
⃗
P
(
i
)
=
[
M
(
i
)
]
⋅
R
⃗
P
m
{{\Delta }^{(i)}}=(\vec{R}_{P}^{(i)}-{{{\vec{R}}}_{E}})\cdot \vec{n},\vec{R}_{P}^{(i)}=[{{M}^{(i)}}]\cdot {{{\vec{R}}}_{Pm}}
Δ(i)=(RP(i)−RE)⋅n,RP(i)=[M(i)]⋅RPm
而鞍线误差为其中的最大值,其计算公式为∶
Δ
p
r
=
max
{
∣
Δ
(
i
)
∣
}
=
max
{
∣
x
P
(
i
)
cos
ϕ
+
y
P
(
i
)
sin
ϕ
−
h
∣
}
{{\Delta }_{pr}}=\max \{\left| {{\Delta }^{(i)}} \right|\}=\max \{\left| x_{P}^{(i)}\cos \phi +y_{P}^{(i)}\sin \phi -h \right|\}
Δpr=max{∣∣∣Δ(i)∣∣∣}=max{∣∣∣xP(i)cosϕ+yP(i)sinϕ−h∣∣∣}
换言之,极值点条件由上式通过数值计算和比较来确定。由此可知,离散运动刚体上一点 P P P在固定平面坐标系中产生一离散点集 { R P ( i ) } \{R_{P}^{(i)}\} {RP(i)},在 { R P ( i ) } \{R_{P}^{(i)}\} {RP(i)}中由三个鞍线拟合特征点确定出唯一鞍线,这三个鞍线拟合特征点所对应的运动刚体位置,称为鞍线拟合特征位置。显然,鞍点规划模型建立了离散运动、刚体上点及其离散轨迹(鞍线拟合特征点)、鞍线(位置)和鞍线误差相互对应关系,为讨论离散点集 { R P ( i ) } \{R_{P}^{(i)}\} {RP(i)}与直线比较的整体几何性质提供了依据。
2.4.3 三位置鞍线
当运动刚体在固定坐标系中仅有三个离散位置时,编号为1、2、3,运动刚体上任意点
P
P
P在固定坐标系中仅产生含有三个离散点
P
(
1
)
{{P}^{(1)}}
P(1),
P
(
2
)
{{P}^{(2)}}
P(2)和
P
(
3
)
{{P}^{(3)}}
P(3)的离散点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)},
i
=
1
,
2
,
3
i=1,2,3
i=1,2,3。依据鞍线拟合模型,调用鞍线子程序AprF,得到各自对应的鞍线,称为三位置鞍线。三个离散点都是鞍线拟合特征点,分布在鞍线两侧,其误差
Δ
\Delta
Δ为相同的最大值,三个位置自然也是鞍线拟合位置。
对于三位置离散轨迹 { R P ( i ) } \{R_{P}^{(i)}\} {RP(i)}, i = 1 , 2 , 3 i=1,2,3 i=1,2,3,依据鞍点规划理论,三位置鞍线误差为最大拟合误差(极大值)最小,而且拟合特征点 P ( 1 ) {{P}^{(1)}} P(1), P ( 2 ) {{P}^{(2)}} P(2)和 P ( 3 ) {{P}^{(3)}} P(3)分布在鞍线的两侧。令三个拟合特征点处的误差相等(实现两侧分布),使得最大拟合误差取得极小值(不一定是最小值)。如下图所示,直线 L 12 , 3 {{L}_{12,3}} L12,3, L 23 , 1 {{L}_{23,1}} L23,1和 L 13 , 2 {{L}_{13,2}} L13,2,称为三位置分布线,依据鞍点规划模型(最大误差最小),取三个三位置分布线误差最小者为三位置鞍线,即 L 23 , 1 {{L}_{23,1}} L23,1。为便于后文的离散运动几何学分析,在此推导三位置分布线误差的代数方程。
对于三位置分布线
L
12
,
3
{{L}_{12,3}}
L12,3,其下标为位置编号,表明特征点
P
(
1
)
{{P}^{(1)}}
P(1)和
P
(
2
)
{{P}^{(2)}}
P(2)位于分布线
L
12
,
3
{{L}_{12,3}}
L12,3一侧,而点
P
(
3
)
{{P}^{(3)}}
P(3)位于分布线
L
12
,
3
{{L}_{12,3}}
L12,3另一侧,则过点
P
(
1
)
{{P}^{(1)}}
P(1)和
P
(
2
)
{{P}^{(2)}}
P(2)的直线方程为∶
(
x
P
(
2
)
−
x
P
(
1
)
)
y
−
(
y
P
(
2
)
−
y
P
(
1
)
)
x
+
y
P
(
2
)
x
P
(
1
)
−
x
P
(
2
)
y
P
(
1
)
=
0
(x_{P}^{(2)}-x_{P}^{(1)})y-(y_{P}^{(2)}-y_{P}^{(1)})x+y_{P}^{(2)}x_{P}^{(1)}-x_{P}^{(2)}y_{P}^{(1)}=0
(xP(2)−xP(1))y−(yP(2)−yP(1))x+yP(2)xP(1)−xP(2)yP(1)=0
P
(
3
)
{{P}^{(3)}}
P(3)到直线
P
(
1
)
P
(
2
)
‾
\overline{{{P}^{(1)}}{{P}^{(2)}}}
P(1)P(2)的距离为:
d
=
∣
(
x
P
(
2
)
−
x
P
(
1
)
)
y
P
(
3
)
−
(
y
P
(
2
)
−
y
P
(
1
)
)
x
P
(
3
)
+
y
P
(
2
)
x
P
(
1
)
−
x
P
(
2
)
y
P
(
1
)
∣
(
x
P
(
2
)
−
x
P
(
1
)
)
2
+
(
y
P
(
2
)
−
y
P
(
1
)
)
2
d=\frac{\left| (x_{P}^{(2)}-x_{P}^{(1)})y_{P}^{(3)}-(y_{P}^{(2)}-y_{P}^{(1)})x_{P}^{(3)}+y_{P}^{(2)}x_{P}^{(1)}-x_{P}^{(2)}y_{P}^{(1)} \right|}{\sqrt{{{(x_{P}^{(2)}-x_{P}^{(1)})}^{2}}+{{(y_{P}^{(2)}-y_{P}^{(1)})}^{2}}}}
d=(xP(2)−xP(1))2+(yP(2)−yP(1))2∣∣∣(xP(2)−xP(1))yP(3)−(yP(2)−yP(1))xP(3)+yP(2)xP(1)−xP(2)yP(1)∣∣∣
三个点
P
(
1
)
{{P}^{(1)}}
P(1),
P
(
2
)
{{P}^{(2)}}
P(2)和
P
(
3
)
{{P}^{(3)}}
P(3)到分布线
L
12
,
3
{{L}_{12,3}}
L12,3的距离相等,从而分布线拟合误差
Δ
12
,
3
{{\Delta }_{12,3}}
Δ12,3 为∶
Δ
12
,
3
=
∣
(
x
P
(
2
)
−
x
P
(
1
)
)
y
P
(
3
)
−
(
y
P
(
2
)
−
y
P
(
1
)
)
x
P
(
3
)
+
y
P
(
2
)
x
P
(
1
)
−
x
P
(
2
)
y
P
(
1
)
∣
2
(
x
P
(
2
)
−
x
P
(
1
)
)
2
+
(
y
P
(
2
)
−
y
P
(
1
)
)
2
{{\Delta }_{12,3}}=\frac{\left| (x_{P}^{(2)}-x_{P}^{(1)})y_{P}^{(3)}-(y_{P}^{(2)}-y_{P}^{(1)})x_{P}^{(3)}+y_{P}^{(2)}x_{P}^{(1)}-x_{P}^{(2)}y_{P}^{(1)} \right|}{2\sqrt{{{(x_{P}^{(2)}-x_{P}^{(1)})}^{2}}+{{(y_{P}^{(2)}-y_{P}^{(1)})}^{2}}}}
Δ12,3=2(xP(2)−xP(1))2+(yP(2)−yP(1))2∣∣∣(xP(2)−xP(1))yP(3)−(yP(2)−yP(1))xP(3)+yP(2)xP(1)−xP(2)yP(1)∣∣∣
对于运动刚体上点
P
P
P的坐标
x
P
m
,
y
P
m
{{x}_{Pm}},{{y}_{Pm}}
xPm,yPm,可得到固定坐标系中点
P
(
1
)
{{P}^{(1)}}
P(1),
P
(
2
)
{{P}^{(2)}}
P(2)和
P
(
3
)
{{P}^{(3)}}
P(3)的坐标,将其代入上式,可得关于
x
P
m
,
y
P
m
,
Δ
12
,
3
{{x}_{Pm}},{{y}_{Pm}},{{\Delta }_{12,3}}
xPm,yPm,Δ12,3的四次代数方程∶
4
(
a
1
x
P
m
2
+
a
1
y
P
m
2
+
a
2
x
P
m
+
a
3
y
P
m
+
a
4
)
Δ
12
,
3
2
−
(
a
5
x
P
m
2
+
a
5
y
P
m
2
+
a
6
x
P
m
+
a
7
y
P
m
+
a
8
)
=
0
4({{a}_{1}}{{x}_{Pm}}^{2}+{{a}_{1}}{{y}_{Pm}}^{2}+{{a}_{2}}{{x}_{Pm}}+{{a}_{3}}{{y}_{Pm}}+{{a}_{4}}){{\Delta }_{12,3}}^{2}-({{a}_{5}}{{x}_{Pm}}^{2}+{{a}_{5}}{{y}_{Pm}}^{2}+{{a}_{6}}{{x}_{Pm}}+{{a}_{7}}{{y}_{Pm}}+{{a}_{8}})=0
4(a1xPm2+a1yPm2+a2xPm+a3yPm+a4)Δ12,32−(a5xPm2+a5yPm2+a6xPm+a7yPm+a8)=0
式中,
a
i
,
i
=
1
,
2
,
.
.
.
,
8
{{a}_{i}},i=1,2,...,8
ai,i=1,2,...,8为系数,可由离散位置参数
(
x
O
m
f
(
i
)
,
y
O
m
f
(
i
)
,
γ
(
i
)
)
,
i
=
1
,
2
,
3
(x_{Omf}^{(i)},y_{Omf}^{(i)},{{\gamma }^{(i)}}),i=1,2,3
(xOmf(i),yOmf(i),γ(i)),i=1,2,3得到。同理,可得分布线
L
23
,
1
{{L}_{23,1}}
L23,1,及其误差
Δ
23
,
1
{{\Delta }_{23,1}}
Δ23,1和分布线
L
13
,
2
{{L}_{13,2}}
L13,2及其误差
Δ
13
,
2
{{\Delta }_{13,2}}
Δ13,2。三个离散点
P
(
1
)
{{P}^{(1)}}
P(1),
P
(
2
)
{{P}^{(2)}}
P(2)和
P
(
3
)
{{P}^{(3)}}
P(3)的鞍线误差
Δ
123
{{\Delta }_{123}}
Δ123为三个分布线误差
Δ
12
,
3
{{\Delta }_{12,3}}
Δ12,3,
Δ
23
,
1
{{\Delta }_{23,1}}
Δ23,1,
Δ
13
,
2
{{\Delta }_{13,2}}
Δ13,2中的最小值,即:
Δ
123
=
min
(
Δ
12
,
3
,
Δ
13
,
2
,
Δ
23
,
1
)
{{\Delta }_{123}}=\min ({{\Delta }_{12,3}},{{\Delta }_{13,2}},{{\Delta }_{23,1}})
Δ123=min(Δ12,3,Δ13,2,Δ23,1)
鞍线误差
Δ
123
{{\Delta }_{123}}
Δ123 也可直接表示为:
Δ
123
=
∣
∣
∣
Δ
23
,
1
+
Δ
13
,
2
∣
2
−
∣
Δ
23
,
1
−
Δ
13
,
2
∣
2
∣
+
Δ
12
,
3
∣
2
−
∣
∣
∣
Δ
23
,
1
+
Δ
13
,
2
∣
2
−
∣
Δ
23
,
1
−
Δ
13
,
2
∣
2
∣
−
Δ
12
,
3
∣
2
{{\Delta }_{123}}=\frac{\left| \left| \frac{\left| {{\Delta }_{23,1}}+{{\Delta }_{13,2}} \right|}{2}-\frac{\left| {{\Delta }_{23,1}}-{{\Delta }_{13,2}} \right|}{2} \right|+{{\Delta }_{12,3}} \right|}{2}-\frac{\left| \left| \frac{\left| {{\Delta }_{23,1}}+{{\Delta }_{13,2}} \right|}{2}-\frac{\left| {{\Delta }_{23,1}}-{{\Delta }_{13,2}} \right|}{2} \right|-{{\Delta }_{12,3}} \right|}{2}
Δ123=2∣∣∣∣∣∣2∣Δ23,1+Δ13,2∣−2∣Δ23,1−Δ13,2∣∣∣∣+Δ12,3∣∣∣−2∣∣∣∣∣∣2∣Δ23,1+Δ13,2∣−2∣Δ23,1−Δ13,2∣∣∣∣−Δ12,3∣∣∣
那么,运动刚体上任意点P的离散轨迹点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)},
i
=
1
,
2
,
3
i=1,2,3
i=1,2,3对应鞍线
L
123
{{L}_{123}}
L123及鞍线误差
Δ
123
{{\Delta }_{123}}
Δ123。对于给定三位置的运动刚体上所有点,都有对应各自的鞍线及其误差,可构造出三位置运动刚体上点-鞍线误差曲面,具有相同鞍线误差值的点采用曲线连接成为等高线,如下图所示。该图的离散运动刚体三个位置数据来源于表2.1中的前三组位置参数。
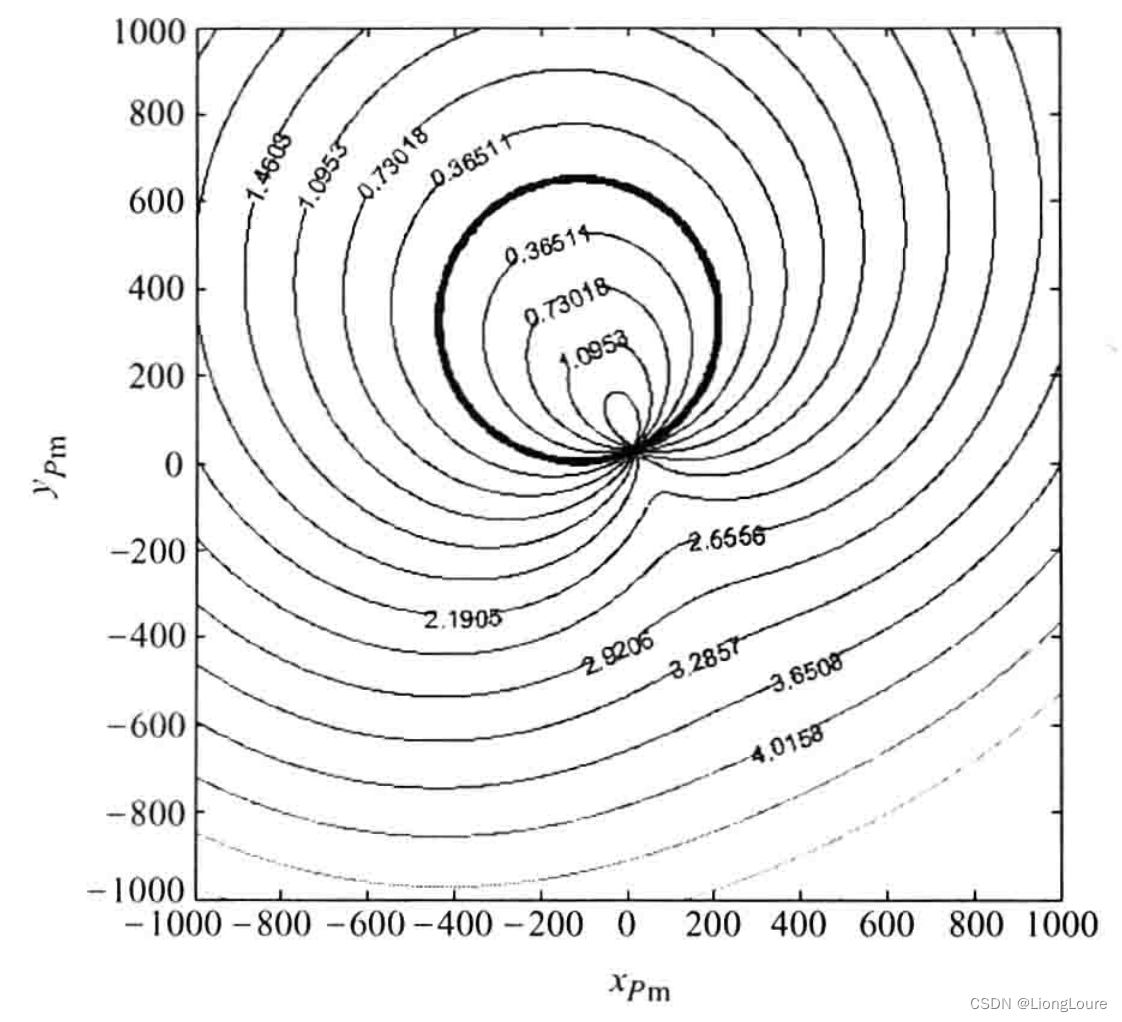
当运动刚体上点对应的鞍线误差值为零时,这些点便为滑点,由给定三位置运动刚体上的滑点构成的滑点曲线恰为圆,如上图中的粗实线所示。
2.4.4 四位置鞍线
给定刚体四个离散位置,序号1、2、3、4,见表2.1中的前四个位置。运动刚体上任意点
P
P
P在固定坐标系中产生对应的四个离散点分别为
P
(
1
)
{{P}^{(1)}}
P(1)、
P
(
2
)
{{P}^{(2)}}
P(2)、
P
(
3
)
{{P}^{(3)}}
P(3)和
P
(
4
)
{{P}^{(4)}}
P(4),依据鞍线拟合模型,调用鞍线子程序AprF,得到各自对应的鞍线,称为四位置鞍线,其误差为
Δ
1234
{{\Delta }_{1234}}
Δ1234。作出四位置鞍线误差曲面与等高线,如下图所示。
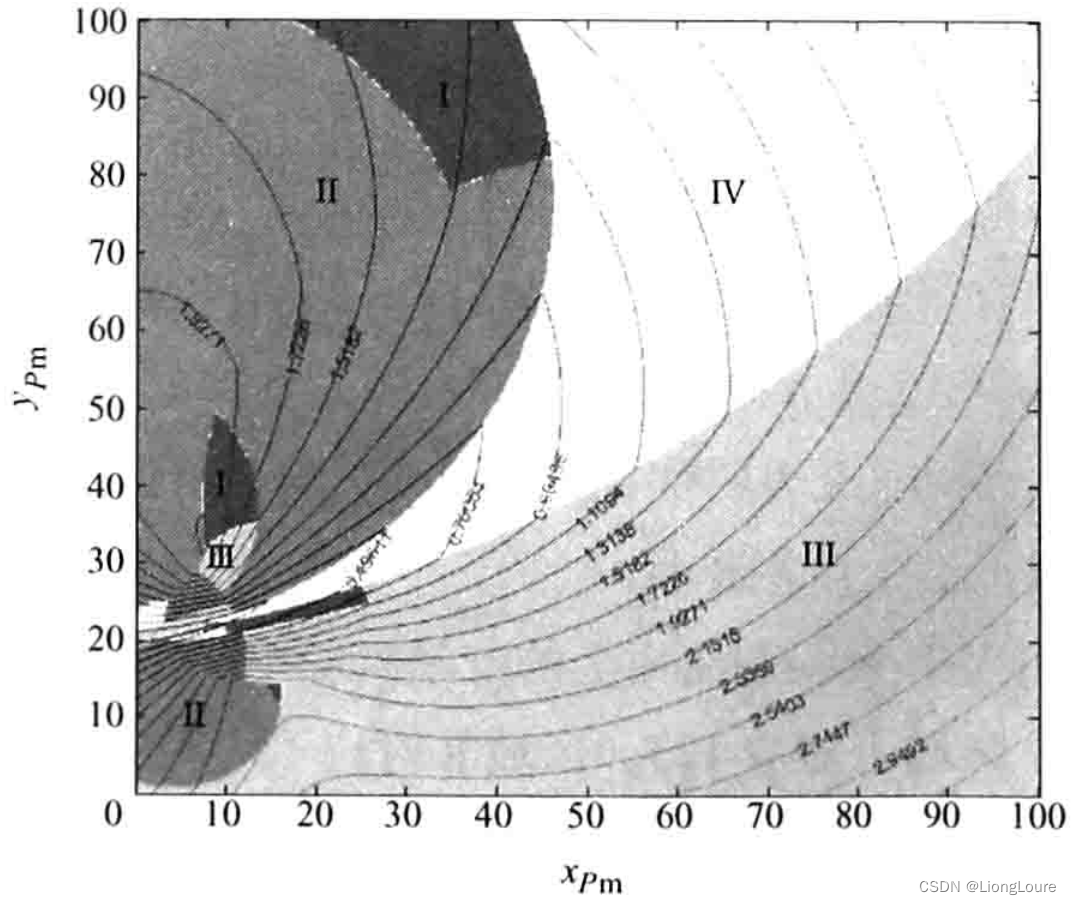
如前所述,运动刚体上任意点在固定坐标系中的离散点集对应的四位置鞍线也只有三个拟合特征点。即四位置鞍线由对应的三个拟合特征点确定,属于该三个拟合特征点对应的三个分布线之一,或者说给定运动刚体四位置,好比在上述三位置基础上增加第四个位置。现在讨论新增加的第四个位置与前三个位置在确定鞍线时的关系。
- 1)第四点
P
(
4
)
{{P}^{(4)}}
P(4)不是离散轨迹的鞍线拟合特征点,对应位置不是拟合特征位置。
即点 P ( 4 ) {{P}^{(4)}} P(4)位于前三个点 P ( 1 ) {{P}^{(1)}} P(1)、 P ( 2 ) {{P}^{(2)}} P(2)、 P ( 3 ) {{P}^{(3)}} P(3)所确定的两平行直线包容区间内,如下图所示。
点 P ( 4 ) {{P}^{(4)}} P(4)对应的误差必小于前三个位置离散点 P ( 1 ) {{P}^{(1)}} P(1)、 P ( 2 ) {{P}^{(2)}} P(2)、 P ( 3 ) {{P}^{(3)}} P(3)的三位置鞍线误差 Δ 123 {{\Delta }_{123}} Δ123,此时 Δ 1234 {{\Delta }_{1234}} Δ1234= Δ 123 {{\Delta }_{123}} Δ123。那么,对于运动刚体上具有同样性质( Δ 1234 {{\Delta }_{1234}} Δ1234= Δ 123 {{\Delta }_{123}} Δ123)的点,分布在运动刚体上某些区域,如上图中所示的区域I,即为123位置点区域。
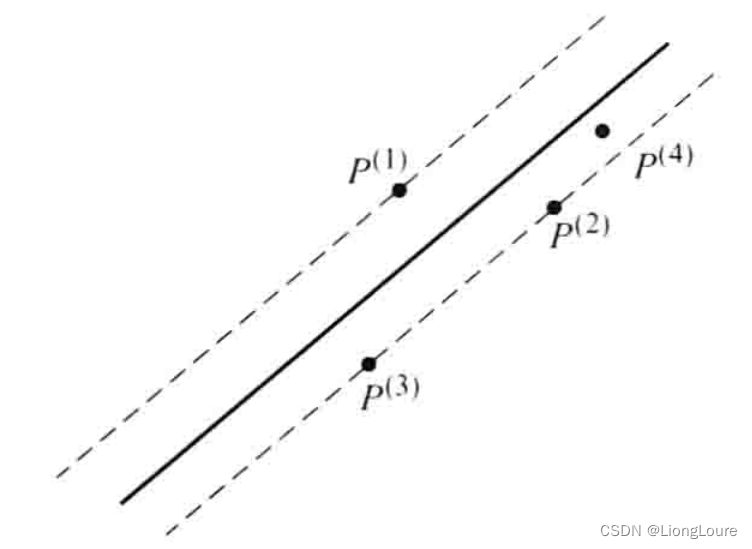
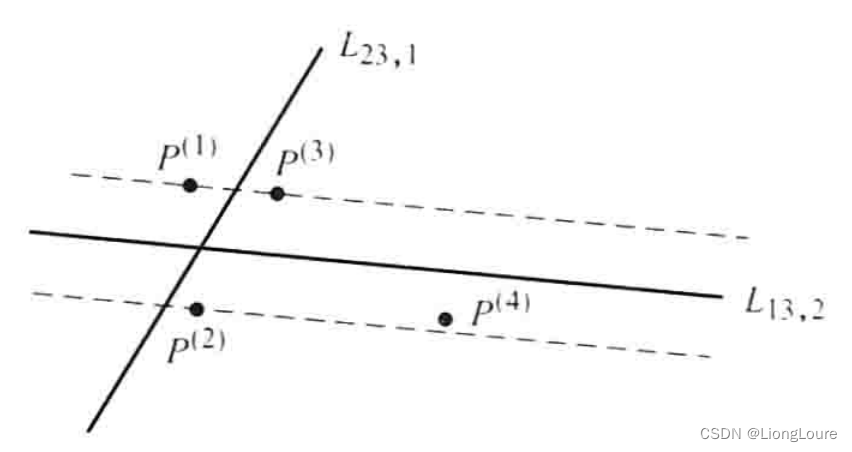
此区域中还有另一种情况,四位置鞍线由 P ( 1 ) {{P}^{(1)}} P(1)、 P ( 2 ) {{P}^{(2)}} P(2)、 P ( 3 ) {{P}^{(3)}} P(3)所确定,但并不是该三位置的鞍线,如下图所示。该三位置鞍线为分布线 L 23 , 1 {{L}_{23,1}} L23,1,是三个分布线中误差最小的, Δ 1234 {{\Delta }_{1234}} Δ1234= Δ 123 {{\Delta }_{123}} Δ123;而四位置鞍线为分布线 L 13 , 2 {{L}_{13,2}} L13,2,属于另一分布线,对应分布情况 P ( 1 ) P ( 3 ) − P ( 2 ) {{P}^{(1)}}{{P}^{(3)}}-{{P}^{(2)}} P(1)P(3)−P(2)。即此时该四位置鞍线 Δ 1234 {{\Delta }_{1234}} Δ1234为三个分布线中的一个 Δ 13 , 2 {{\Delta }_{13,2}} Δ13,2,不一定是三位置分布线误差最小的。
- 2)第四点
P
(
4
)
{{P}^{(4)}}
P(4)是离散轨迹的鞍线拟合特征点,对应位置是拟合特征位置。
由第四个位置和前三个位置中的两个构成三个拟合特征位置,共有三种可能组合情况∶ 124 124 124、 134 134 134和 234 234 234。对于三位置运动刚体上所有点,和前面三位置 123 123 123一样,可得到对应鞍线及鞍线误差,并可构造三位置运动刚体上点-鞍线误差的四次代数曲面。在四位置运动刚体上一点 P P P处,轨迹上四点的鞍线误差必为最小误差,对应拟合特征位置组合三种情况,每种情况下有三个分布线,如三位置 124 124 124,存在三个分布线误差 Δ 12 , 4 {{\Delta }_{12,4}} Δ12,4、 Δ 14 , 2 {{\Delta }_{14,2}} Δ14,2和 Δ 24 , 1 {{\Delta }_{24,1}} Δ24,1。所以,三种位置组合共有9条分布线,哪种情况才有可能成为四位置鞍线误差,需要从四个离散轨迹点 P ( 1 ) ∼ P ( 4 ) {{P}^{(1)}}\sim{{P}^{(4)}} P(1)∼P(4)全局来看,其鞍线误差应满足最大误差最小。
如四位置鞍线误差曲面与等高线图中所示四位置鞍线误差曲面上的若干区域中,每个区域对应着鞍线拟合特征位置的不同组合,例如,区域I对应 123 123 123,区域II对应 124 124 124,区域Ⅲ对应 134 134 134,区域Ⅳ对应 234 234 234。在这四个区域中,每个区域内刚体上点对应不同三位置组合。由于离散运动刚体上的点是连续的,从区域I(123)变化到区域Ⅱ(124)时,边界上点同样应该具有两个区域的特性,其离散轨迹点(四个点)都是拟合特征点(鞍线误差),以便形成与相邻区域对应的鞍线及其误差以适应相邻区域过渡。 例如,两区域界限点,对应误差相等的两条鞍线(鞍线定义只有一条),或鞍线有两个解,即两条误差相同的分布线。将相邻区域的鞍线误差曲面方程联立,如 Δ 123 {{\Delta }_{123}} Δ123= Δ 124 {{\Delta }_{124}} Δ124,由分布线拟合误差和鞍线误差可解得边界方程。一般情况下,边界曲线为六次代数曲线。三个或四个区域边界曲线的交点,则有三个或四个鞍线,并且误差都相等,表明此点对应多条鞍线(误差相同、方位不同)。特殊地,边界点对应的多个鞍线重合(同一条分布线)时,边界曲线退化为圆曲线,鞍线误差曲面二阶连续(相切地过渡),否则相交。
如前所述,四位置的鞍线误差曲面由四个三位置分布线误差曲面的分片组合,而每片都属于四次代数曲面,存在多个峰谷。从整体上比较四位置与三位置的鞍线误差曲面,三位置存在一条误差为零的等高线——滑点曲线,为一圆,相当于河谷;而四位置的等高线则没有,仅有一个鞍线误差为零的谷底点,即滑点(四点共线,误差为零),相当于把河流变成河床,露出一潭水的河谷。


![[附源码]java毕业设计中小企业人力资源管理系统](https://img-blog.csdnimg.cn/b9bf0f1de8db4079bb2ac3fdaaaff4d2.png)