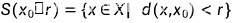它的基本思想是将函数看作向量,从而将函数空间转化为向量空间,进而研究函数空间的性质。泛函分析的主要内容包括:线性空间、内积空间、赋范空间、希尔伯特空间、算子理论、谱理论、函数空间等。
空间与算子
度量空间
赋范空间和巴拿赫空间
线性算子
内积空间和希尔伯特空间
哈恩-巴拿赫定理
一致有界性定理
开映射定理
闭图定理
谱论
赋范空间中的算子
紧算子
自伴算子
无界算子
无界算子
应用
压缩
逼近
度量空间
度量空间的定义
四条公理
开球 闭球 球面
对于度量空间

球面可以是一个空集
开集 闭集
有界集:称A为有界集,若存在一个开球,使得A属于这个开球
内点:称x0为集合G的内点,若存在一个开球B(x0,r)属于G
开集:称G为开集,若G中的每一个点都是它的内点
任意个开集的并是开集,有限个开集的交是开集
闭集:开集的补集就是闭集
任意个闭集的交是闭集,有限个闭集的并是闭集
接触点:点x0称为A的接触点,若存在一个x0的开球与A的交不为空集。(点x0可以属于A,也可以不属于A)
闭集:开集的补集就是闭集。(若用接触点定义闭集就是,A的接触点的全体称为A的闭包)
聚点:点x0称为点A的聚点,若存在点x0的任意一个开球与A\{x0}的交不为空集。(聚点一定是接触点,但接触点不一定是聚点。)
稠密集:称B在A中稠密,若A包含于B的闭包。
可分:一个空间称为可分的,若这空间中存在一个可数的稠密子集。
列紧集:称A为列紧集,若A中的每一个无穷点列都有一个收敛的子列
拓扑空间
连续映射
若在定义域的距离空间中存在一个开集,经过映射T,在另一个距离空间定义的距离下是任意小的
连续映射定理
度量空间X到度量空间Y中的映射T,当且仅当Y的任意开子集的逆像是X中的开子集时,才是连续的
柯西序列
度量空间X=(X,d)中的序列(x_n),如果对于任意给定的正数\epsilon,都存在N=N(\epsilon),使得对于所有的m,n>N,有d(x_m,x_n)<\epsilon,则称(x_n)是柯西序列(基本序列).
完备度量空间
空间X中的每个柯西序列都是收敛序列,则X是完备度量空间
等距映射与等距空间