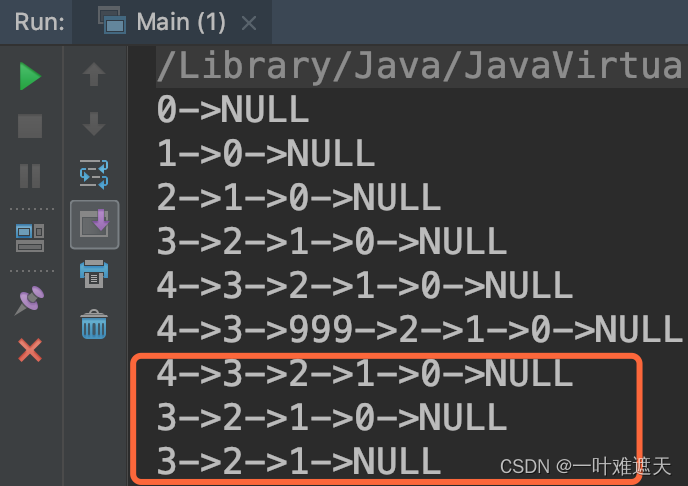
数列特点
无限个数
特定顺序
数列和集合区别
集合可以乱序,数列不行
集合出现重复元素依然相同,数列出现新的重复元素就不相等
[1,2,3,4]=[1,2,3,3,4]
对集合来说相等,对数列来说不相等。
数列的表示形式

求数列的单调性
作差,作商,求导,列举法,把极限和某项比较。
有界数列有上界和下界
如何证明一个数列无界?
eg:比较审敛法
2^n+1>2^n
2^n趋于无穷,2^n+1趋于无穷
证明数列收敛
直接证明数列极限
找出N和 的关系
的关系

夹逼准则

夹逼准则的推论:如果数列的绝对值趋近于0,数列趋于零。
当数列的符号无法确定时,用绝对值证
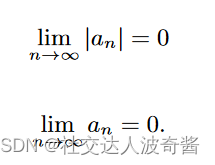
洛必达法则,无穷/无穷或0/0
洛必达法则是:量级的比较和同除n^p有异曲同工之妙。
数列单调且有界,数列收敛

数列和的收敛
数列和收敛,数列趋近于0,但数列趋近于0,数列不一定收敛。

积分试验:
被积的函数是递减函数,函数的反常积分收敛,等于函数各项和收敛。
(两个其实表示的都是函数围成的面积。)
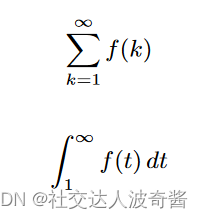
使用时先判断是否是递减,在再使用。递减是为了保证大小关系

去掉最左边那一块,右边能全部移到左边,此时曲线面积大于数列和面积,证明反常积分收敛,就能证明数列和收敛(从第二项开始的和收敛和第一项开始收敛是一样的)
比较审敛法:同反常积分。
交错级数判别法:
交错级数:一正一负
1,-2,3,-4...
-1,2,-3,-4……
证明交错级数收敛
证明数列的绝对值:1.单调递减或最终单调递减 2.收敛于0。
一些公式及技巧
单调减的指数函数乘幂函数的收敛于0

证明:一直洛必达法则直到幂函数的系数为0。
由于指数的变化速率太快,使得幂函数的a是1或者k都一样。

 的结果
的结果

n为项数,C为欧拉常数用来调和级数
习题
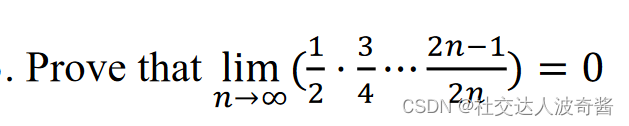
累乘无法相消, 的极限趋向于1。
的极限趋向于1。
这意味着无法对每一项放缩成再相乘 只能整体放缩
只能整体放缩
注意:


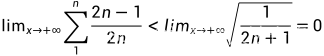
巧妙的放缩!