电子技术——CMOS反相器的动态响应

数字系统的速度（例如计算机）取决于其构成逻辑门的信号传播速度。因为反相器是数字逻辑门电路的基础，反相器的传播速度是一个很重要的特性。

传播延迟

传播延迟定义为反相器响应他的输入所需要的时间。特别的，先让我们对反相器输入一个理想的阶跃函数，获得对应的响应，如图：

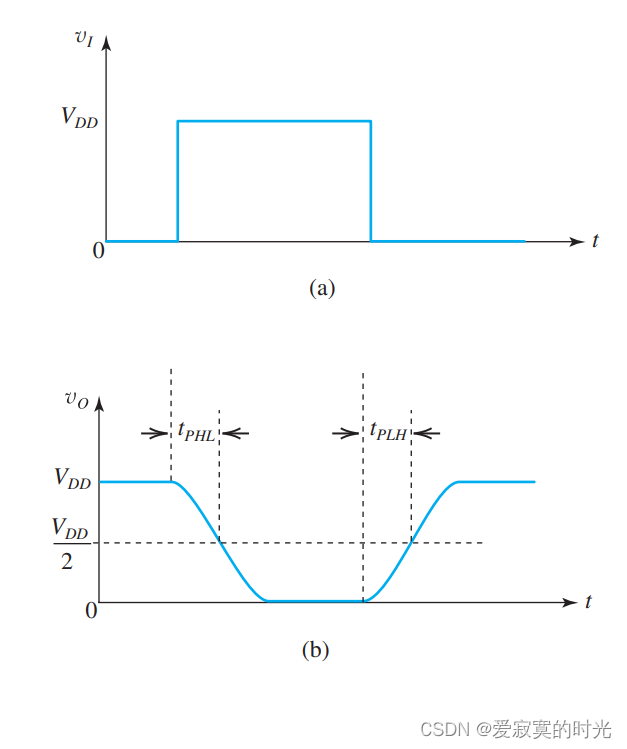
1. 输出信号不再是理想的阶跃函数，而是具有一个圆滑的边界，也就是说，反相器需要一定的时间切换输出状态。我们说响应有有限的上升和下降时间。
2. 输入和输出存在一定的时间延迟。若我们定义输出响应的“开关点”为状态过渡的中点，我们就可以定义反相器的传播延迟。注意到存在两种传播延迟，一种是从高电平到低电平的延迟 $t_{PHL}$ 以及从低电平到高电平的 $t_{PLH}$ ，通常两个延迟时间不必相等。

传播延迟定义为：

$$t_P\equiv \frac{1}{2}(t_{PLH}+t_{PHL})$$

定义完传播延迟之后，我们定义反相器的最大开关速度，从图（b）中我们发现，最小的周期为：

$$T_{min}=t_{PHL}+t_{PLH}=2t_P$$

则最大开关频率为：

$$f_{max}=\frac{1}{T_{min}}=\frac{1}{2t_P}$$

到此为止，读者一定想知道造成CMOS反相器传播延迟的原因。这仅仅是因为需要给电路中的电容充放电所需要的时间，电容存在于MOSFET内部的电容、线间电容以及逻辑门之间的输入容抗。稍后我们会解释电容如何决定 $t_P$ ，现在我们预备两个关键的知识：

1. 一个分析动态响应的关键表达式为 $I\Delta t=\Delta Q=C\Delta V$ 。这说明，对一个电容器充 $\Delta Q$ 的电荷量需要时间 $\Delta t$ ，此时电容器两端电压上升 $\Delta V$ 。
2. 对于一个时间常数为 $\tau$ 的低通型或高通型STC电路来说，若输入是一个阶跃函数，则输出的瞬态响应为 $y(t)=Y_{\infty }-(Y_{\infty }-Y_{0+})e^{-t/\tau }$ ，这里 $Y_{\infty }$ 是一个有限值，这个值代表了响应的终值， $Y_{0+}$ 表示响应的起始值当 $t=0$ 的时候。

现在，我们可以正式的定义CMOS反相器的传播延迟，若输入的激励是一个具有 上升下降时间 的阶跃函数，那么我们称 $\frac{1}{2}(V_{OL}+V_{OH})$ 为输入的翻转点，反相器的在输入翻转点处开始动态响应，从这里开始计时，直到输出也达到翻转点停止，这一段时间称为响应的上升或下降时间，分别记为 $t_{PLH}$ 和 $t_{PHL}$ ，这里 $P$ 是延迟的意思，而 $LH$ 是从低到高， $HL$ 是从高到低。通常定义传播延迟为 $t_{PLH}$ 和 $t_{PHL}$ 的平均值。并且，我们称过渡时间为从一个响应的10%到90%的时间，如图：

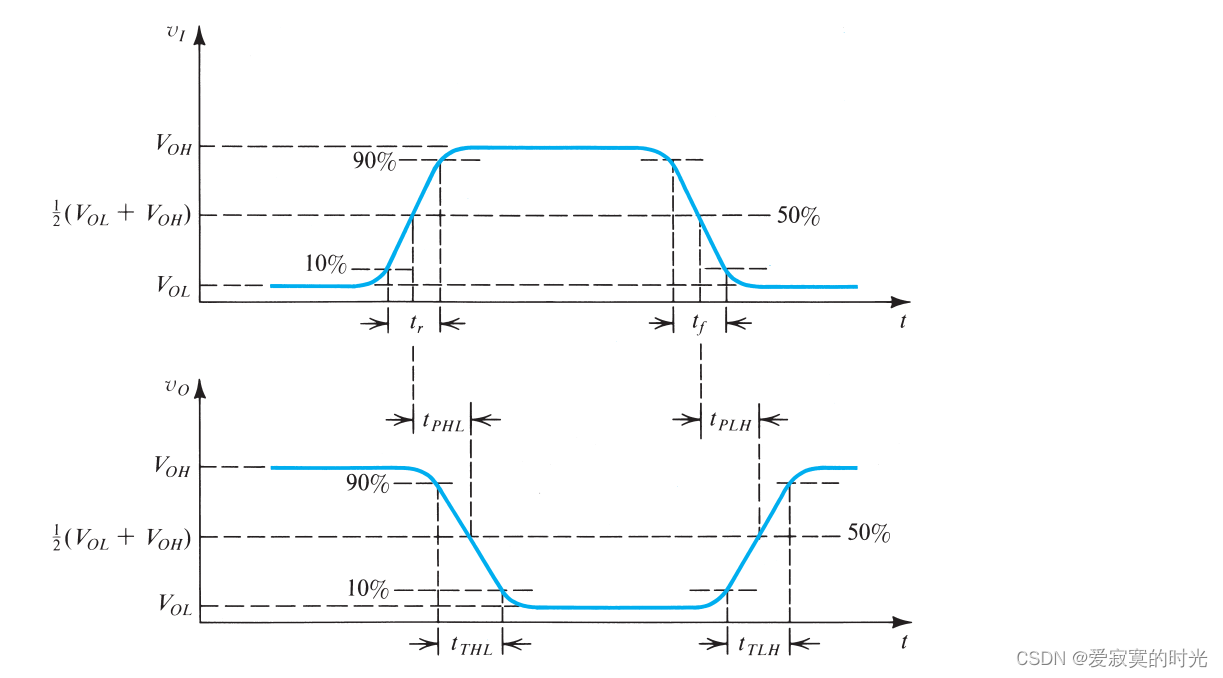
决定CMOS反相器的传播延迟

我们通过一下两个步骤决定CMOS反相器的传播延迟：

1. 将电路中所有的电容替换为从CMOS反相器的输出端到地的等效电容 $C$ 。
2. 计算 $t_{PLH}$ 和 $t_{PLH}$ 以及 $t_P$ 。

我们反过来学习者两个步骤，首先我们先学习如何计算传播延迟，之后我们学习如何等效电容。

下图展示了仅有输出端到地的电容 $C$ ：

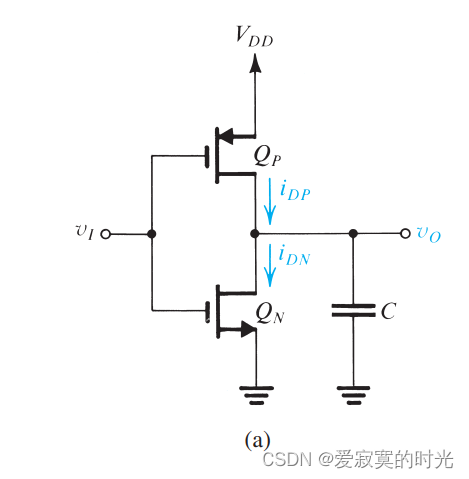
为了方便计算，我们假设输入的激励是一个理想的阶跃函数，对应的响应如图：

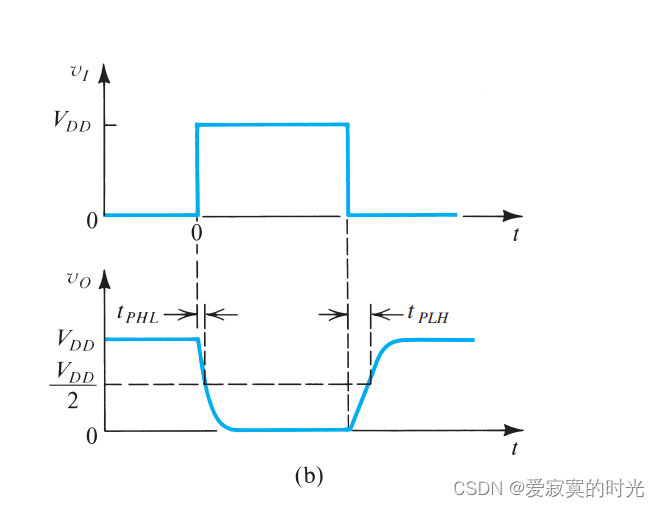
因为这个电路是对称的，因此分析从低到高和从高到地是相似的。当 $t=0$ 的时候，此时 $v_I$ 从 $0$ 上升至 $V_{DD}$ 。此时 $Q_P$ 截止而 $Q_N$ 导通，如图：

我们发现，此时的输出端电压的起始值为 $V_{DD}$ 。因此在 $t=0+$ 的时候 $Q_N$ 处于饱和区，提供一个关于电容 $C$ 的放电电流，下图展示了放电过程中， $i_{DN}$ 与 $v_O$ 的关系：

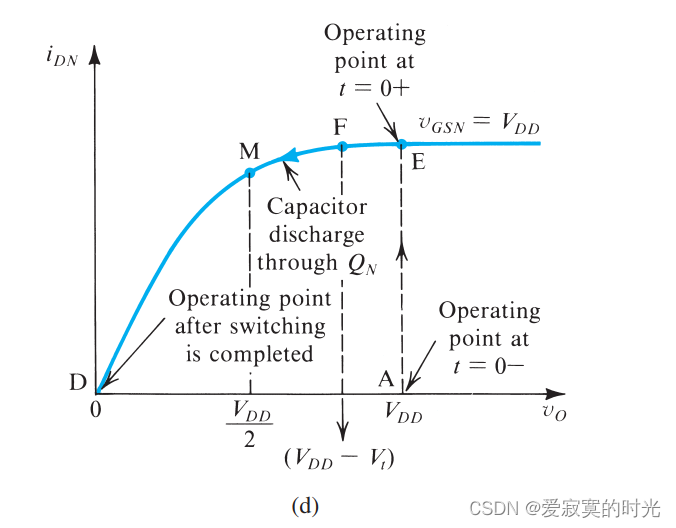
在这里我们只关心 $t_{PHL}$ 时间，也就是上图中从点E到点M所需要的时间，在EF段，此时 $Q_N$ 处于饱和区，超过F点之后，进入三极管区。

一个简单的方法是我们可以计算EM段的平均电流 $I_{av}$ ，之后，通过方程：

$$I_{av}{t}_{PHL}=C[V_{DD}-(V_{DD}/2)]$$

决定：

$$t_{PHL}=\frac{C{V}_{DD}}{2I_{av}}$$

平均电流 $I_{av}$ 可以通过下面的表达式估算：

$$I_{av}=\frac{1}{2}[i_{DN}(E)+i_{DN}(M)]$$

这里：

$$i_{DN}(E)=\frac{1}{2}{k}_n^{\prime }(W/L{)}_n(V_{DD}-V_{tn}{)}^2$$

并且：

$$i_{DN}(M)=k_n^{\prime }(W/L{)}_n[(V_{DD}-V_{tn})(\frac{V_{DD}}{2})-\frac{1}{2}(\frac{V_{DD}}{2}{)}^2]$$

我们假设 ${\lambda }_n=0$ 带入上式得到：

$$t_{PHL}=\frac{{\alpha }_{n}C}{k_n^{\prime }(W/L{)}_n{V}_{DD}}$$

这里的 ${\alpha }_n$ 是：

$${\alpha }_n=2/[\frac{7}{4}-\frac{3V_{tn}}{V_{DD}}+(\frac{V_{tn}}{V_{DD}}{)}^2]$$

${\alpha }_n$ 通常在1-2的范围内。

同样的分析方法可以计算 $t_{PLH}$ 得到：

$$t_{PLH}=\frac{{\alpha }_{p}C}{k_p^{\prime }(W/L{)}_p{V}_{DD}}$$

这里：

$${\alpha }_p=2/[\frac{7}{4}-\frac{3|V_{tp}|}{V_{DD}}+|\frac{V_{tp}}{V_{DD}}{|}^2]$$

最后，传播延迟为：

$$t_p=\frac{1}{2}(t_{PHL}+t_{PLH})$$

通过上面的表达式我们可以总结一下几点：

1. $t_P$ 的两个分量可以通过条件 $W/L$ 来使得相同。
2. 因为 $t_P$ 正比于 $C$ 。设计师应该努力减小 $C$ 的值，这可以通过减小沟道长度，或是减小信号线长或是其他寄生电容。通过合理的电路布局可以减小潜在的寄生电容。
3. 使用合适的工艺，使得增加 $k^{\prime }$ 的值，以减少传播延迟。但是， $C_{ox}$ 也会增加。
4. 使用更大的宽长比。同样的，增加元件的体积同样会增加电容值。
5. 更大的 $V_{DD}$ 可以减小 $t_P$ 。然而，通常情况下， $V_{DD}$ 受到工艺的限制，而不是设计师随便决定。

另一种替代方法

下面的表达式来自于深亚微米工艺，主要由速度饱和效应引起，之后我们会介绍，饱和效应降低了MOS管在饱和区的电流，提升了传播延迟时间。为了估计此情况的传播延迟，我们可以使用下面的方法。

下图展示了一个替代估算的方法原理图：

我们将MOS管替换成一个等效的电阻，通过：

$$t_{PHL}=0.69R_{N}C$$

以及：

$$t_{PLH}=0.69R_{P}C$$

一个经验的估算公式为：

$$R_N=\frac{12.5}{(W/L{)}_n}k\Omega$$

$$R_P=\frac{30}{(W/L{)}_p}k\Omega$$

这个公式适用于CMOS 0.25um 和 0.18um 以及 0.13um 的工艺。

对于更实际的情况，输入具有上升和下降时间，此时 $0.69$ 十分接近于单位一，此时：

$$t_{PHL}\simeq R_{N}C$$

$$t_{PLH}\simeq R_{P}C$$

最后，需要注意的是，以上分析都是基于估算，并不总是会产生精确的结果，必要请需要使用电路仿真。

决定等效容性负载C

下图是我们研究的原理图：

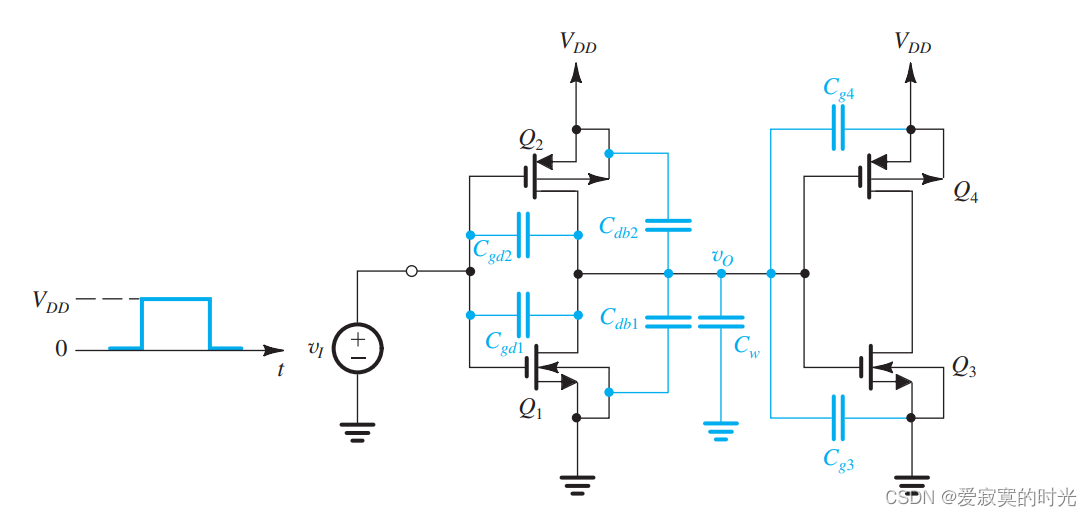
这里 $Q_1$ 和 $Q_2$ 作为驱动CMOS反相器而 $Q_3$ 和 $Q_4$ 作为负载CMOS反相器，我们在这里只列出关于输出节点的电容，特别的 $C_w$ 称为 线间电容 。

1. 首先栅极-漏极间电容 $C_{gd1}$ 可以等效为对地 $2C_{gd1}$ 因子 $2$ 是由于米勒效应。如图：
   
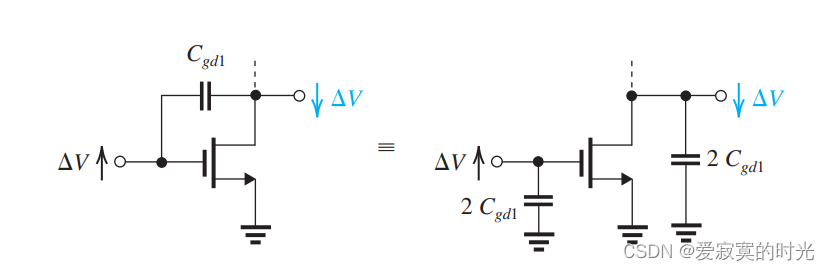
   同理对于 $C_{gd2}$ 。
2. 通常来说体极的电压是固定的，因此体极-漏极直接的电容，可以直接等效为对地的电容。
3. 此时我们假设第二个CMOS反相器的状态还没有切换，所以输入容抗等于： $C_{g3}+C_{g4}=(WL{)}_3{C}_{ox}+(WL{)}_4{C}_{ox}+C_{gsov3}+C_{gdov3}+C_{gsov4}+C_{gdov4}$ 。

所以，等效电容为：

$$C=2C_{gd1}+2C_{gd2}+C_{db1}+C_{db2}+C_{g4}+C_{g3}+C_w$$