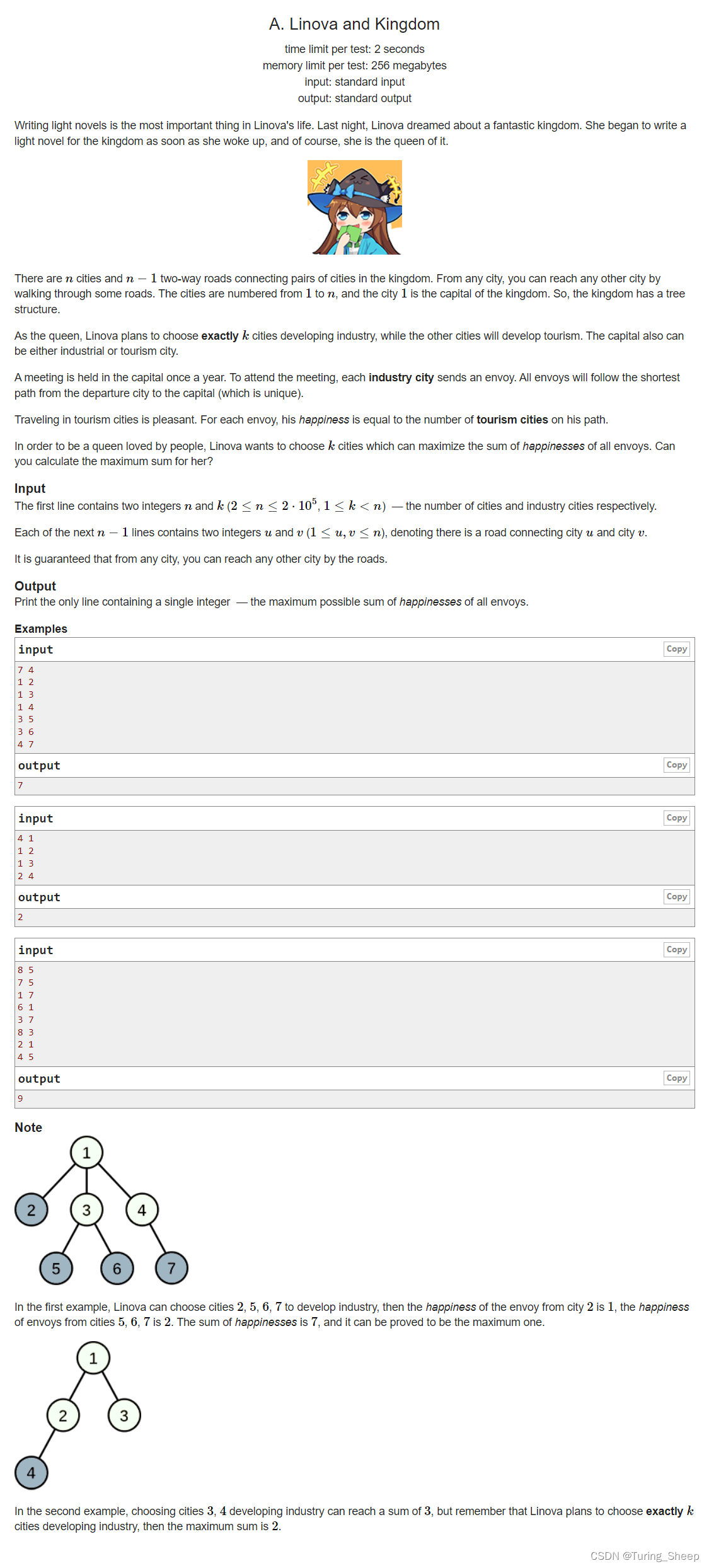
一、问题

二、思路

这道题的大意就是，给我们一棵树，我们需要在树上选择$k$个点，然后让$k$个信使从我们选取的$k$个点向第一个点出发。

我们把我们选取的k个点涂为黑色，剩下的点涂为白色。

我们从黑色点出发，如果经过白色的点，我们的快乐值就会加1，如果经过的黑色的点，我们的快乐值不变。

那么对于$k$个点而言，在他们向第一个点出发的过程中，都会有一个属于自己的快乐值。

我们需要求出这些快乐值的和的最大值。

那么思路是什么呢？

如果不管路上的黑色点的话，我们要想快乐值很大的话，我们就需要选择深度最深的点，即从叶子节点开始选。

除此之外，我们需要观察出，在最优解中，如果一个点被选择了，那么他的子节点必定被选择。

为什么呢？

我们假设最优解中，存在一个点$i$，我们选择了它，但是它的子节点中有一个没有被选。

我们从两个角度开始考虑。

这个子节点到根节点的距离肯定大于我们的节点$i$到根节点的距离，因此，我们这个子节点的快乐值肯定是大于等于节点$i$的快乐值的。（当且仅当$i$和该子节点直接相连时，取到等号）

另外，由于我们选择了节点$i$，所有节点$i$中被选的子节点在经过$i$的时候是不加快乐值的，如果我们不选$i$，而是选未被选择的$i$的子节点的话，那些经过点$i$不经过该子节点的点的快乐值就会整体+1。
而那些即经过该子节点又经过点$i$的点的快乐值是不变的，所以整体的快乐值就会增大。

因此，我们假设的情况并不是最优解。故我们的结论成立：如果一个点被选了，那么这个点的子节点一定被选。

对于一个被选的点而言，它对答案的贡献是什么呢？

首先，这个点会使得它的子节点的快乐值都-1，然后它到根节点的距离是他的贡献值。那么总的贡献就是$dep[i]-son[i]$

我们只需要所有点的总贡献，然后取前$k$个累加输出即可。

三、代码

#include<bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 2e5 + 10;
int n, k;
vector<int>g[N];
int cnt[N], dep[N], son[N];
ll ans;

int dfs(int u, int deep, int father)
{	
	int sum = 0;
	for(int i = 0; i < g[u].size() ; i++ )
	{
		int j = g[u][i];
		if(j == father)continue;
		sum += dfs(j, deep + 1, u);
	}	
	dep[u] = deep;
	son[u] = sum;
	return sum + 1;
}
void solve()
{
	cin >> n >> k;
	for(int i = 0; i < n - 1; i ++ )
	{
		int a, b;
		cin >> a >> b;
		g[a].push_back(b);
		g[b].push_back(a);
	}
	dfs(1, 0, -1);
	for(int i = 1; i <= n; i ++ )
		cnt[i] = dep[i] - son[i];
	sort(cnt + 1, cnt + 1 + n);
	reverse(cnt + 1, cnt + 1 + n);
	
	for(int i = 1; i <= k; i ++ )
		ans += cnt[i];
	cout << ans << endl;

}

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);

	solve();
}