Stochastic Approximation —Stochastic gradient descent 随机近似方法的详解之（四）随机梯度下降

郑重声明：本系列内容来源 赵世钰(Shiyu Zhao)教授的强化学习数学原理系列，本推文出于非商业目的分享个人学习笔记和心得。如有侵权，将删除帖子。原文链接：https://github.com/MathFoundationRL/Book-Mathmatical-Foundation-of-Reinforcement-Learning

SGD算法在机器学习领域被广泛应用。We will show that SGD is a special RM algorithm and the mean estimation algorithm is a special SGD algorithm. 假定我们要解决下面这个优化问题：

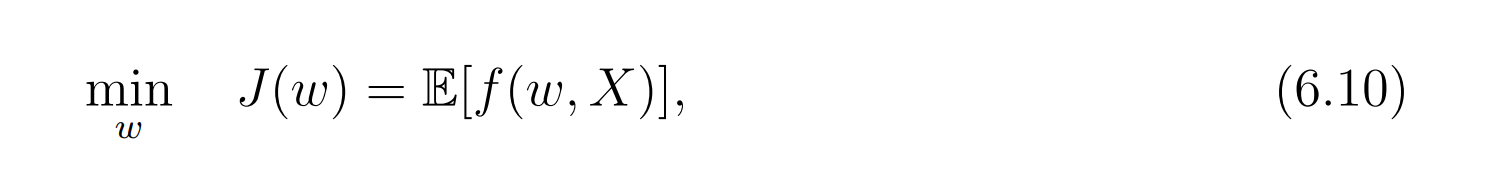
$w$ 是要被优化的参数，$X$是个随机变量，两者都可以是向量。

在函数f是凸函数的情况下，求解上述问题的直接方法是梯度下降。

右边式子的期望的梯度是什么呢？

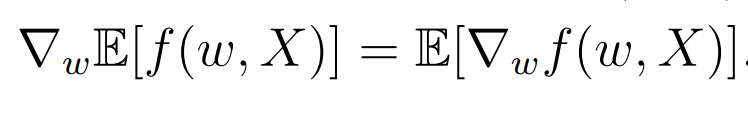
于是有下面的式子：

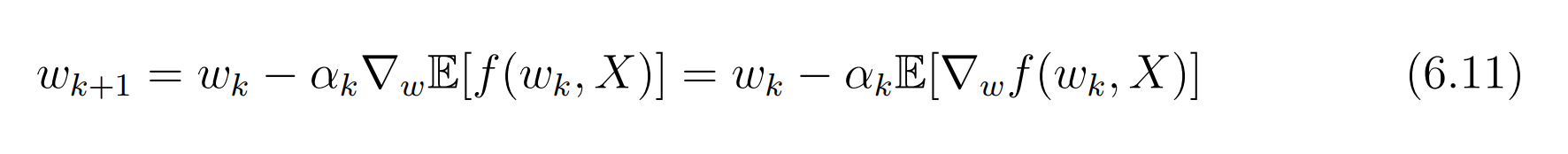
然而，这个期望的梯度实际中很难求到。
Another way is to collect a large number of iid samples { x i } i n = 1 \{x_i\}^n_i=1 {xi​}in​=1 of X so that the expected value can be approximated as :

$\mathbb{E}\left[{\nabla }_{w}f\left(w_k,X\right)\right]\approx \frac{1}{n}{\sum }_{i=1}^n{\nabla }_{w}f\left(w_k,x_i\right)$

通过这样的近似，(6.11)公式就变成了：

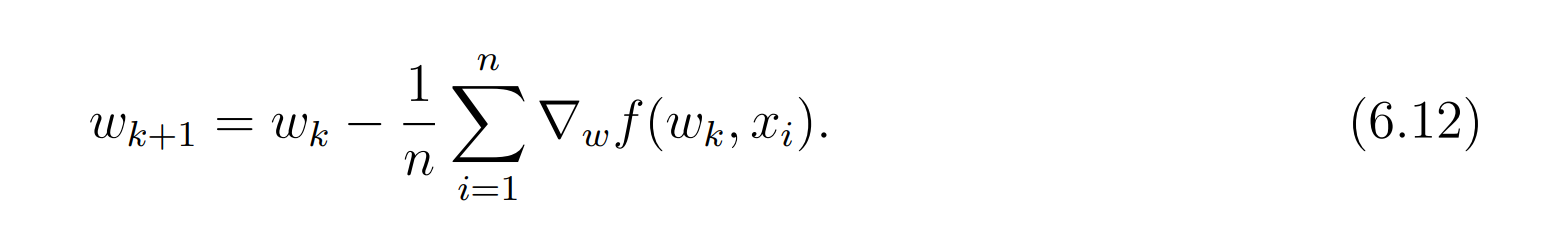
This algorithm is called batch gradient descent (BGD) because it uses all the samples as
a single batch in every iteration. 注意，BGB（批梯度）算法的每一次迭代用的都是全部的样本。

然而事实上样本是一个一个被收集的。我们希望$w$能够实时的随着抽样的进行而更新。于是有了下面的随机梯度算法：

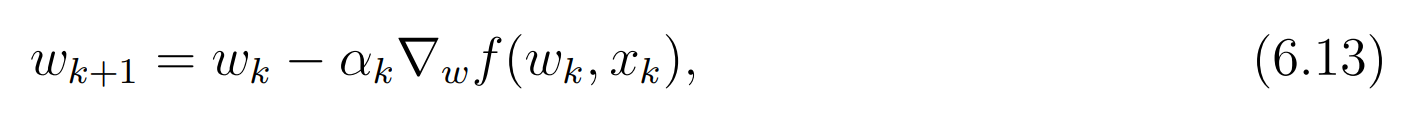
随机二字的含义是抽样过程的随机性，也就是说，这个方法依赖于随机抽样。

这个梯度项的替换，能否保证最优解的收敛性呢？

看了上面的解释，豁然开朗，原来二者之间差了一个噪声项，${\alpha }_k{\eta }_k$这一个扰动项是收敛到0的。所以这个扰动项的加入并没有破坏收敛性。

SGD‘s apply to mean estimation

我们来说明 mean estimation 其实是一种特殊的SGD。

首先，把mean estimation表示成如下的优化问题：

在这种情况下，期望的表达式，或者说样本的分布情况并不知道，自然就无法求$\mathbb{E}$ 对于w的导数了。

sgd的做法是什么呢？

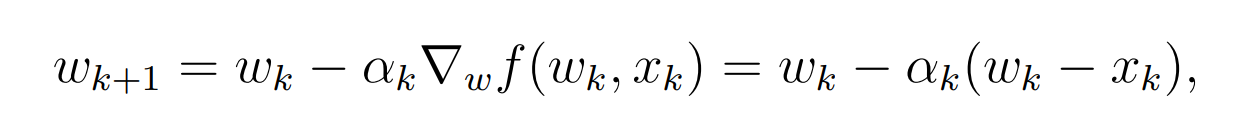
SGD收敛性的分析

由于抽样是随机的，所以估计是不准确的。问题是，SGD的收敛是随机的吗，是缓慢的吗？

先来看看批梯度和随机梯度之间的相对误差：

如果${\delta }_k$很小，那么我们可以认为随机梯度的效果和标准梯度下降相似。注意，下面公式中，分母上新增加的那个项，因为是在最优解处，所以梯度值为0。第二个等号成立是因为中值定理。

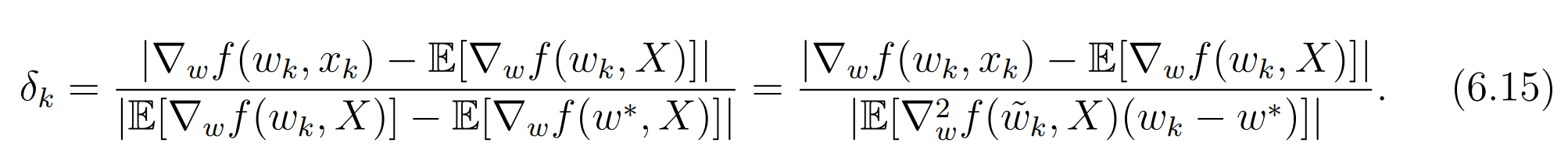
如何理解最后这个结论呢？

也就是说，w的初始值离最优值距离比较远的时候，SGD的算法的表现会更像梯度下降；而w的初始值离最优值距离比较接近的时候，SGD的算法的收敛会表现出一定的随机性。

在下面这个均值估计问题中，随机变量$X$代表二维空间的随机变量。注意是二维哦！！
我们可以看到不同的梯度下降算法的收敛过程。

下面描述了实验的设定：

可以看到，SGD确实在接近最优值的时候，展示出了一定程度的随机性。

SGD的确定性公式

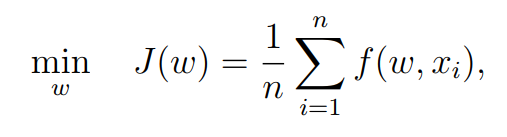
在这种情况下，解决这个问题的梯度下降算法就变成了下面的形式：

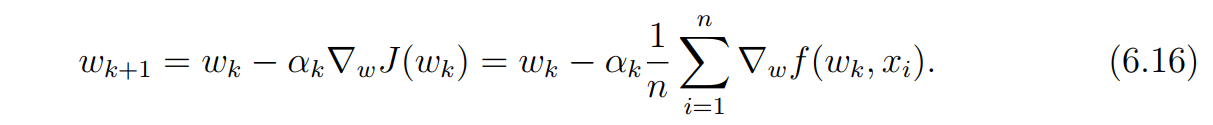
假定集合很大并且我们一次只能抽一个样本，这种情况下，我们肯定还是希望能够渐进地实时更新最优解。
然后，我们就可以用下面的迭代算法了：

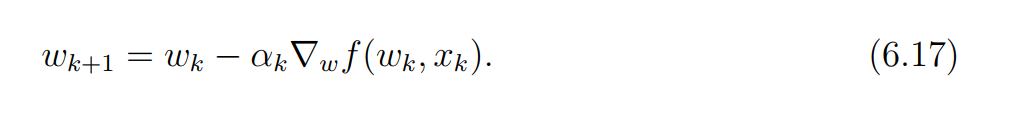
解决的办法是什么呢？
通过引入样本集合上的随机变量$X$，可以把确定性的优化问题变成随机形式的：

BGD, SGD, and Mini-batch GD

以均值估计任务为例子来看看三种算法：

需要注意的是当MBGD的m=n的时候，它和BGD仍然不一样。为啥呢：

另外，MBGD的收敛速度一般来说比SGD更快：

Summary

知道为啥要反复讨论均值估计问题吗？
因为在强化学习中，状态价值和动作价值都被定义为随机变量的期望。

强化学习算法相比于其他的问题求解方法的特点优势在哪里呢？

也就是说，强化学习不需要知道目标函数具体的表达是什么。它是一个黑盒方法，只需要知道目标函数的输入和输出。著名的随机梯度下降算法就是一种特殊的强化学习算法。

随机梯度下降的基本要点是什么呢？

它可以在不知道随机变量的分布的情况下通过样本求解到一个无偏的解。

数学直观上看，随机梯度是把梯度下降算法中的期望的梯度替换成了一个随机梯度。