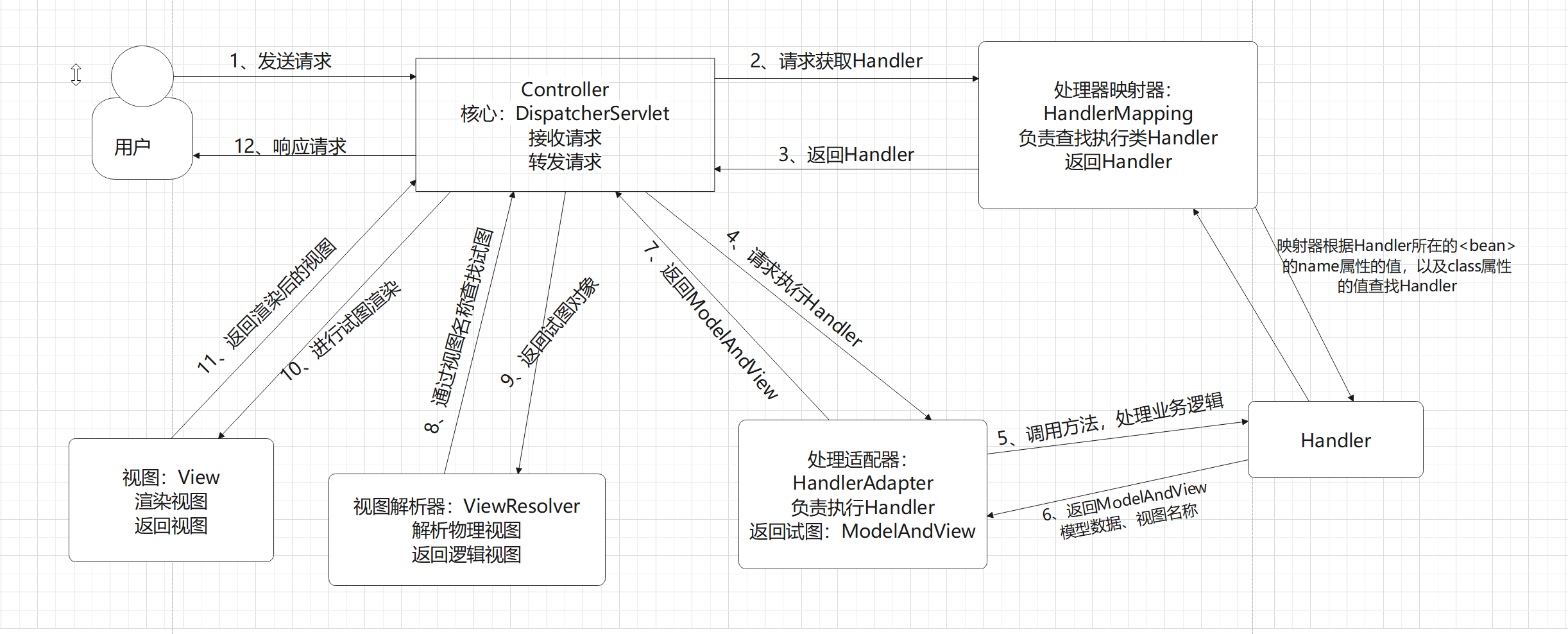
目录
前言
概念
堆排序的实现
1.建堆
(1)堆向上调整算法
(2)堆的向下调整算法
2. 利用堆删除思想来进行排序
3.堆排序的时间复杂度
4.源码
总结
前言
前边我们学习了堆的实现,对堆的每个接口都进行了详细的讲解,所以这篇文章就来看一看堆到底有哪些应用。
概念
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法:
- 大顶堆:每个节点的值都大于或等于其子节点的值,在堆排序算法中用于升序排列;
- 小顶堆:每个节点的值都小于或等于其子节点的值,在堆排序算法中用于降序排列;
堆排序的平均时间复杂度为 Ο(nlogn)。
我们之前学习的冒泡排序的时间复杂度为o(n^2),此处的堆排序确是Ο(nlogn),这样直接看并不能看出堆排序的优势,如果我们使用数字代入就会发现,如果我们有1000个数,进行排序时,冒泡排序是100万次,若是堆排序只需1万次,对于更大的数差别也会更大,所以堆排序是很有优势的。
堆排序的实现

1.建堆
我们根据上节课的学习,我们知道了向上调整算法和向下调整算法,他们都可以建立一个堆。
我们要切记,需要升序排列时要建一个大堆,需要降序排列时要建一个小堆。
(1)堆向上调整算法
现在我们给出一个数组,逻辑上看做一颗完全二叉树。我们从第二个位置向上调整,直到最后一个位置的数为止。
void hpSort(int* a, int n)
{
assert(a);
//从第二个数开始向上调整
for (int i = 1; i < n; i++)
{
adjustUp(a, i);
}
}
(2)堆的向下调整算法
现在我们给出一个数组,逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆。向下调整算法有一个前提:左右子树必须是一个堆,才能调整。
 有人可能认为向下调整算法的时间复杂度为o(n*log2n),其实并不是,时间复杂度其实为o(n),由于在倒数第二层时,每个元素只调整了一次,倒数第三层调整了两次,也可以通过数学公式来证明,通过错位相减法,最终得到了向下调整算法的时间复杂度为o(n)。
有人可能认为向下调整算法的时间复杂度为o(n*log2n),其实并不是,时间复杂度其实为o(n),由于在倒数第二层时,每个元素只调整了一次,倒数第三层调整了两次,也可以通过数学公式来证明,通过错位相减法,最终得到了向下调整算法的时间复杂度为o(n)。
void hpSort(int* a, int n)
{
assert(a);
//从非叶子结点开始向下调整
for (int i = (n-1)-1/2; i >= 0; i--)
{
adjustDown(a, n, i);
}
}从非叶子结点开始调整,可以从最后一个结点的父节点处开始,进行向下调整,直至调整到根节点。
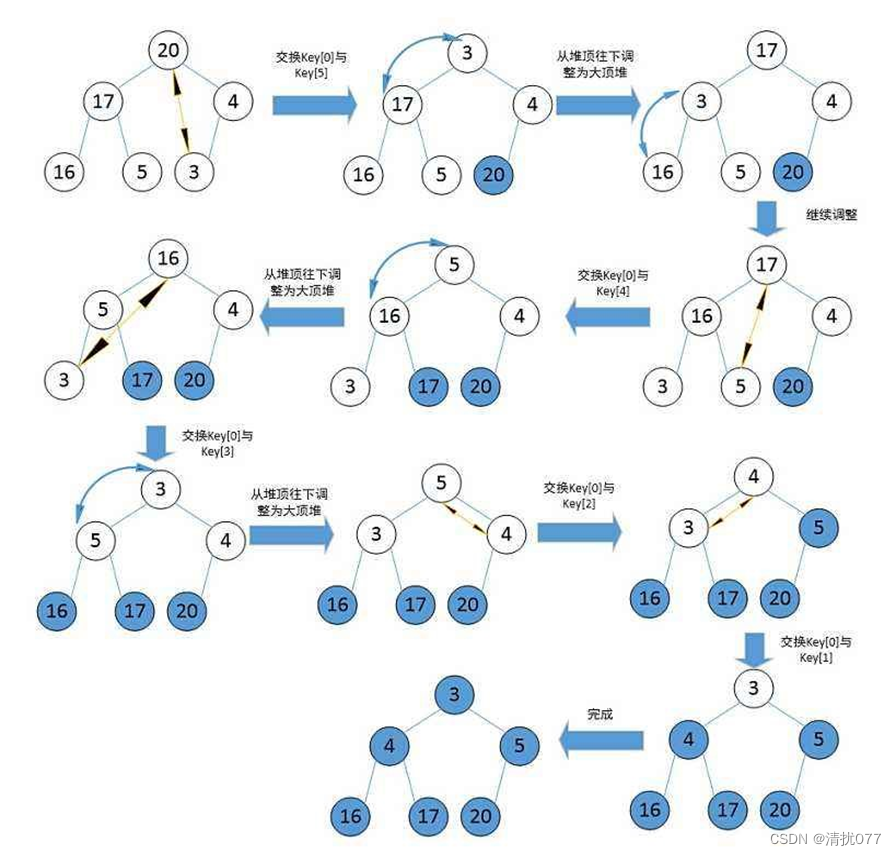
2. 利用堆删除思想来进行排序
(1)当我们要对数据进行降序排列时,我们先建立一个小堆,即父节点的数据小于子节点的数据。
(2)将最后一个结点与第一个结点互换,此时得到的最后一个结点的数据就是最小的数。
(3)此时对第一个结点向下调整,使其恢复成为一个小堆,此时堆顶元素就是整个堆中次小的数。
(4)此时,我们把最后一个结点与原来结点分离,只是看作分离,只是将其余结点从新进行之前的操作,直至堆的大小为1。
void hpSort(int* a, int n)
{
assert(a);
//从第二个数开始向上调整
/*for (int i = 1; i < n; i++)
{
adjustUp(a, i);
}*/
//从非叶子结点开始向下调整
for (int i = (n-1)-1/2; i >= 0; i--)
{
adjustDown(a, n, i);
}
for(int end=n - 1 ; end > 0 ; end--)
{
swap(&a[0], &a[end]);
adjustDown(a, end ,0);
}
}
3.堆排序的时间复杂度
我们知道了向下调整算法来建堆的时间复杂度为o(n),所以我们选择向下调整算法来建堆,在建完堆之后,我们就进行交换并且向下调整,排序的时间复杂度为o(n*log2n),所以总和的时间复杂度为o(n*log2n)。
4.源码
hpsort.c
void hpSort(int* a, int n)
{
assert(a);
//从第二个数开始向上调整
/*for (int i = 1; i < n; i++)
{
adjustUp(a, i);
}*/
//从非叶子结点开始向下调整
for (int i = (n-1)-1/2; i >= 0; i--)
{
adjustDown(a, n, i);
}
for(int end=n - 1 ; end > 0 ; end--)
{
swap(&a[0], &a[end]);
adjustDown(a, end ,0);
}
}test.c
void test1()
{
//TestTopk();
int a[] = { 70, 56, 30, 25, 15, 10, 75, 33, 50, 69 };
for (int i = 0; i < sizeof(a) / sizeof(a[0]); ++i)
{
printf("%d ", a[i]);
}
printf("\n");
hpSort(a, sizeof(a) / sizeof(a[0]));
for (int i = 0; i < sizeof(a) / sizeof(a[0]); ++i)
{
printf("%d ", a[i]);
}
printf("\n");
}总结
今天我们学习了堆排序的概念,实现,以及时间复杂度,过两天我会继续发布关于各种排序的文章,希望大家支持。

![English Learning - L2-3 英音地道语音语调 小元音 [ʌ] [ɒ] [ʊ] [ɪ] [ə] [e] 2023.02.27 周一](https://img-blog.csdnimg.cn/c9544eb009684aab87d231f7ce9b3f1f.png)