写在前面
原码、反码、补码是计算机组成原理中的概念,是计算机网络的基础知识之一。这些概念是为了处理二进制数的符号位而引入的,常用于计算机中的整数运算,也常用于数据存储和传输等领域。因此,了解和掌握这些概念对于理解计算机网络和计算机组成原理都是非常重要的。
目录
写在前面
初步认识
发展历程
为什么要使用
有什么作用
如何计算 原码、反码、补码
例题
初步认识
在计算机中,整数通常使用原码、反码和补码表示。这三种表示方式都是用二进制位表示数字,但有不同的规则来表示正负号。
-
原码(sign-magnitude representation):最高位表示符号位,0表示正数,1表示负数,其余位表示数值大小。例如,+5的原码是00000101,-5的原码是10000101。
-
反码(ones' complement):正数的反码和原码相同,负数的反码是将原码中除符号位外的所有位按位取反。例如,+5的反码是00000101,-5的反码是11111010。
-
补码(two's complement):正数的补码和原码相同,负数的补码是将原码中除符号位外的所有位按位取反后加1。例如,+5的补码是00000101,-5的补码是11111011。
补码表示法是计算机中最常用的表示带符号整数的方式,其好处是可以用同一种方式进行加减运算,且减法可以转换成加法。例如,5-3可以转换成5+(-3),即00000101+11111101=00000010。此外,补码可以用来表示0,而原码和反码都会出现两个0的情况,分别对应+0和-0。
发展历程
在计算机的发展过程中,原码、反码和补码的概念逐渐形成和发展。
最早的计算机采用的是原码表示带符号数,即用二进制的最高位表示符号位,0表示正数,1表示负数。但是原码表示法存在着两个0的表示,即正数的0和负数的0。
为了解决这个问题,人们又发明了反码表示法。反码表示法是将负数的符号位不变,其他位按位取反,这样便能够解决正数和负数0的问题。但是反码表示法存在着减法运算的问题,即在进行减法运算时需要将被减数的符号位取反再加上减数的符号位。
后来,人们又发明了补码表示法。补码表示法是将负数的符号位不变,其他位按位取反再加1,这样既解决了0的问题,也能够解决减法运算的问题,因此成为了计算机中最常用的带符号整数表示法。
总的来说,原码、反码和补码是带符号整数的三种不同表示方法,随着计算机的发展,补码表示法逐渐成为了计算机中最常用的带符号整数表示法。
为什么要使用
计算机使用原码、反码和补码来表示带符号整数,主要是因为计算机中的运算是基于补码进行的。
在计算机中,加法和减法都是通过对二进制数的补码进行运算来实现的,这样可以将加法和减法转化为相同的运算。同时,补码的表示范围与原码相同,而且可以避免原码的符号位运算问题,使得运算更加方便。
另外,补码还有一个特点,就是它只有一个零,而原码和反码有正零和负零之分,这样会给计算带来很多问题,例如在比较大小时需要进行特殊的处理。而补码只有一个零,可以避免这些问题。
因此,使用原码、反码和补码可以使计算机进行带符号整数的运算更加方便、准确和统一,避免了很多计算问题。
有什么作用
常见的有符号整数表示方法包括原码、反码和补码。
1. 原码是一种最基本的数值表示方法,用于表示有符号的整数。在原码中,数值的最高位用于表示符号,0表示正数,1表示负数。例如,+7的原码为0000111,-7的原码为1000111。原码的表示方法最直观,计算机也最容易实现,但是它存在一些缺陷,主要体现在以下几个方面:
- 加减法不方便:在原码中,加减法需要分别考虑符号位和数值部分,这样计算起来比较繁琐。例如,对于+7和-5进行相加,需要先将它们的符号位进行运算,然后再对它们的数值部分进行运算,最终得到的结果为+2,其计算过程为:0000111 + 1000101 = 1001100,即7 - 5 = 2。
- 0有两种表示方法:在原码中,0既可以表示为0000000,也可以表示为1000000。这种情况下,计算机在进行运算时需要特殊处理,否则会导致运算结果错误。
- 为了解决原码存在的问题,人们提出了反码和补码的概念。
2. 反码是一种表示带符号整数的方式,它是在原码的基础上进行改进的。与原码相同的是,反码的二进制数最高位仍然用来表示符号,0表示正数,1表示负数。但是,对于负数的表示,反码做了一些特殊处理。
具体来说,正数的反码与原码相同。例如,+5的原码和反码都是00000101。但是,对于负数,反码是符号位不变,其余各位取反。例如,-5的原码是10000101,那么它的反码就是11111010。
反码的加减法只需要进行二进制的加法即可。例如,计算+3-2,可以将3和2的反码相加,再将结果取反得到最终的反码。具体过程如下:
+3的反码:00000011 -2的反码:11111101 相加得到:00000010 取反得到:11111101 所以,+3-2的结果的反码为11111101,对应的十进制数是-1。
反码的缺点是0还是有两种表示方法,分别是00000000和11111111。这是因为在原码中,0的符号位为0,在反码中,0的符号位为1,其余各位为0。因此,正零的反码为00000000,负零的反码为11111111。这种情况在计算机中可能会引起混淆,因此出现了补码的表示方式,它能够避免这个问题。
3. 补码是在反码的基础上进行了改进,主要解决了反码的问题,如反码的加减法中出现的溢出问题。补码的加减法与二进制的加减法是一致的,不需要考虑符号位。正数的补码和原码相同,负数的补码是其反码加1。
举个例子,假设要将数-5表示为补码形式。首先,将-5的绝对值表示为二进制形式,即0101,然后将其按位取反得到反码1010,最后将反码加1得到补码1011。因此,-5的补码为1011。
在计算机中,补码广泛应用于计算机算术运算和数据存储中。由于补码的加减法和二进制的加减法一致,可以方便地实现算术运算。此外,使用补码还可以避免0的两种表示方法,简化了计算机的处理。
总的来说,原码、反码和补码都是计算机中用于表示有符号整数的方法。它们的区别在于对于负数的表示方式不同,以及0的表示方法的差异。
原码是最简单的表示方法,使用二进制数的最高位表示符号。正数的原码和二进制数相同,负数的原码是其绝对值的二进制表示在最高位加上符号位1。原码的缺点是加减法不方便,需要单独考虑符号位,而且0有两种表示方法。
反码在原码的基础上改进,正数的反码和原码相同,负数的反码是符号位不变,其余各位取反。反码的加减法只需要进行二进制的加法即可,但是0还是有两种表示方法。
补码在反码的基础上进一步改进,正数的补码和原码相同,负数的补码是其反码加1。补码的加减法可以直接进行二进制的加法,且0只有一种表示方法,因此补码被广泛应用于计算机中。
在计算机中,一般使用补码表示有符号整数。因为补码具有很好的加减法性质和唯一的0表示方法,同时还能够方便地进行位运算和处理溢出等问题。
如何计算 原码、反码、补码
在计算机中的数据通常都是用二进制位来存储,其中的0和1都是比特,8个比特可以组成一个字节,一个字节可以表示256种不同的状态,可以用来表示整数、字符等数据类型。而原码、反码、补码,就是带有符号的整数。与字节有着密不可分的关系。
在计算之前我们先要学习进制转换
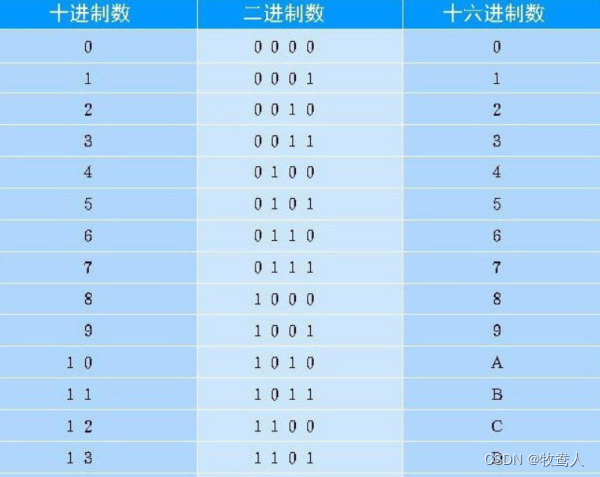
2的零次方=1,2的一次方=2,2的二次方=4,2的三次方=8,2的四次方=16,2的五次方=32,2的六次方=64,2的七次方=128,
00000000 ——对应上面的次方
2进制是由8个比特组成,每个比特以2的次方计算最为方便。比如56,先计算出56处于2的几次方之间。可以看出56大于32小于64,所以2的五次方是1,56-32=24 。24大于16小于32,所以2的四次方也是1,24-16=8,刚好等于2的三次方,所以56=2的三次方+2的四次方+2的五次方=00111000
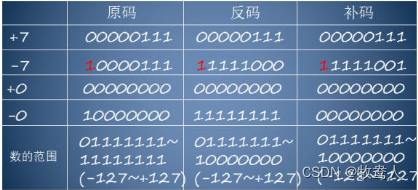
原码可以表示的数值是 -127到127 ,共计256个数。
反码也可以表示的数值是 -127到127 ,共计256个数。
补码可以表示的整数范围与原码和反码相同,都是在n个比特位中能表示的整数范围。但是,补码具有唯一的0表示法和良好的加减法性质,因此在计算机中被广泛应用。在使用补码表示法时,通常采用32位或64位的补码表示,这样可以表示更大的整数范围,同时保证计算机操作的高效性和精确性。
计算原码、反码、补码还需要掌握以下几个步骤:
- 确定数值的绝对值,转换成二进制数(忽略符号位)
- 确定数值的符号位,0表示正数,1表示负数
- 根据原码、反码、补码的定义,得到对应的码值
以十进制数-12为例,下面介绍如何计算原码、反码、补码:
- 确定数值的绝对值,即12的二进制表示为:1100
- 确定数值的符号位,因为-12是负数,所以符号位为1
- 计算原码:将符号位和绝对值合并,得到原码:1100 1100
- 计算反码:对于负数,反码是符号位不变,其余各位取反,得到反码:1111 0011
- 计算补码:对于负数,补码是反码加1,得到补码:1111 0100
同样地,以十进制数+12为例,下面介绍如何计算原码、反码、补码:
- 确定数值的绝对值,即12的二进制表示为:1100
- 确定数值的符号位,因为+12是正数,所以符号位为0
- 计算原码:将符号位和绝对值合并,得到原码:0100 1100
- 计算反码:对于正数,反码和原码相同,得到反码:0100 1100
- 计算补码:对于正数,补码和原码相同,得到补码:0100 1100
例题
- 假设要表示数值-23,我们要怎么算出他的原码、反码、补码
-23 的绝对值是23,转换成二进制是00010111.
符号位为1,表示负数,因此需要进行补码表示
因此-23的原码为 10010111
因此-23的反码为 11101000
因此-23的补码为 11101001
- 假设要表示数值+42,我们要怎么计算出他的原码、反码、补码
+42的绝对值为42,转换成二进制是00101010
符号位为0,表示正数
因此+42的原码为 00101010
因此+42的反码为 00101010
因此+42的补码为 00101010
- 假设要表示数值-223,我们要怎么计算出他的原码、反码、补码
-223的绝对值为223,转换成二进制是1101 1111
符号位为负,表示负数,因此需要进行补码表示
因此-223的原码为1000000011011111——因为-223是负数所以需要在字节前面加1,而223的8个比特的第8位已经是1了,所以我们要在给它一个字节;用1000000011011111的方式呈现它的原码
因此-223的反码为1111111100100000——因为反码是要将原码的1000000011011111因为在反码中,符号位不变,数值部分按位取反。
因此-223的补码为1111111100100001——因为负数补码需要在反码的基础上加1。