前言

前边077带着大家学习了树与二叉树的相关概念，这篇文章我们来实现一个二叉树的顺序结构。

二叉树的顺序结构

普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储，需要注意的是这里的堆和操作系统 虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段。

与前边的栈类似，数据结构中的堆与地址空间的堆是完全不同的，是两个学科中的名词。

堆的概念及结构

将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

堆的性质：

堆中某个节点的值总是不大于或不小于其父节点的值；

堆总是一棵完全二叉树。

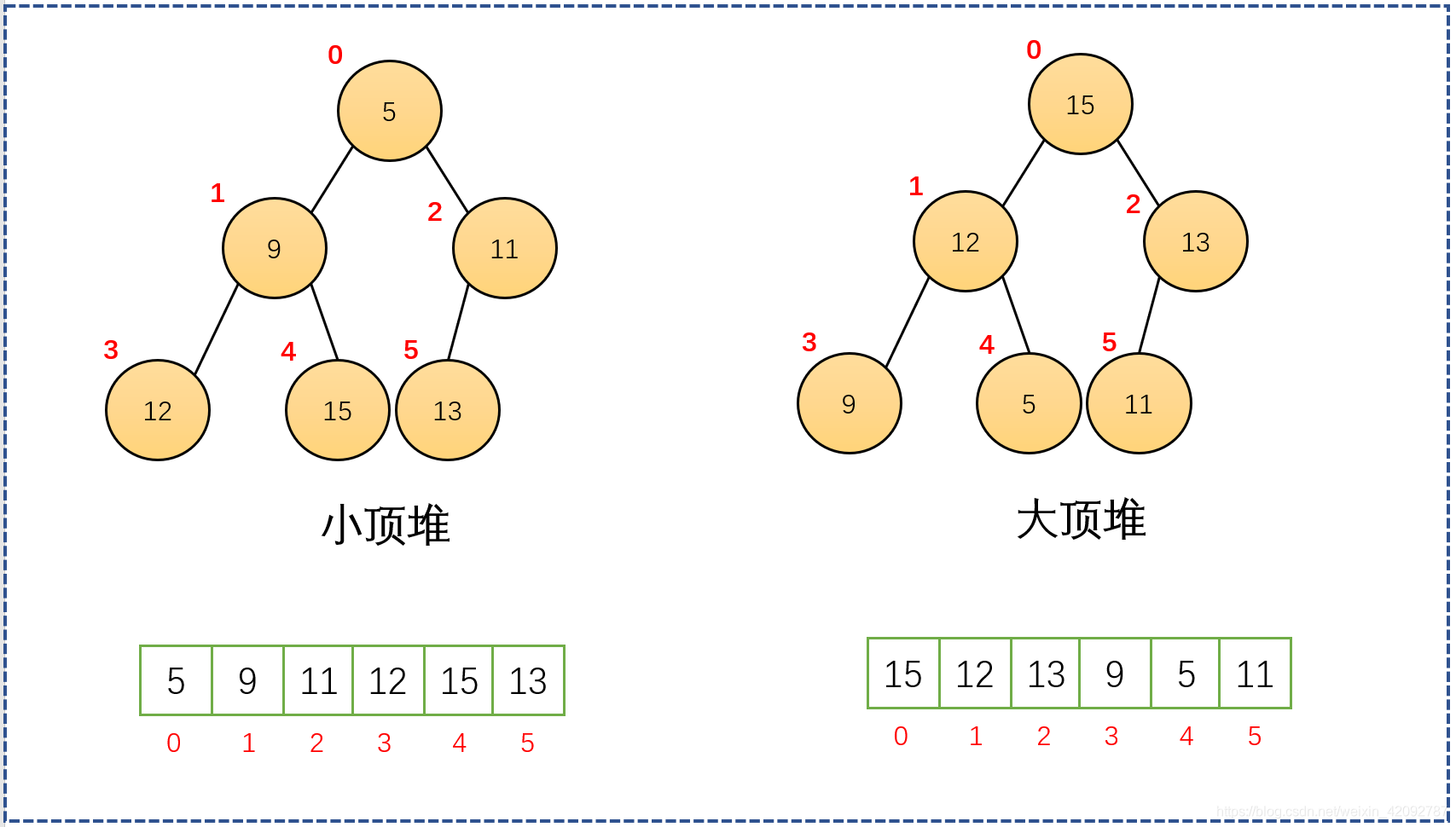
数据结构堆的概念&&堆排序的思想以及算法过程详解（图文）_LifeGoesOn-CSDN博客_数据结构建堆过程

小堆，又叫小根堆，小顶堆，顾名思义就是这个堆的根节点数据是最小的，而且每一个父节点的数据都要小于子节点的数据，有一个不满足都不是小堆。

大堆就是根节点最大的堆，堆中每一个父节点的数据都是大于子结点的数据。

堆的实现

堆的接口实现

1.堆的结构

typedef int hpDataType;
typedef struct heap
{
	hpDataType* a;
	int size;
	int capacity;
}hp;

堆是顺序的二叉树，所以要定义一个顺序表，在物理上就是一个顺序表，在逻辑上确是一个二叉树，也就是堆。

2.初始化

void hpInit(hp* ph)
{
	assert(ph);
	ph->a = NULL;
	ph->capacity = ph->size = 0;
}

3.销毁顺序表

void hpDestory(hp* ph)
{
	assert(ph);
	free(ph->a);
	ph->a = NULL;
	ph->capacity = ph->size = 0;
}

4.向上调整

void adjustUp(hpDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] > a[parent])
		{
			int tmp = a[child];
			a[child] = a[parent];
			a[parent] = tmp;

			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

使用向上调整算法可以随意插入数据，并且还不改变堆，还为一个小堆或者大堆，我这里实现的是一个大堆。

5.堆的插入

void hpPush(hp* ph, hpDataType x)
{
	assert(ph);
	if (ph->size == ph->capacity)
	{
		hpDataType newCapacity = ph->capacity == 0 ? 4 : ph->capacity * 2;
		hpDataType* tmp = (hpDataType*)realloc(ph->a, sizeof(hpDataType)*newCapacity);
		if (tmp == NULL)
		{
			perror("realloc fail/n");
			exit(-1);
		}

		ph->a = tmp;
		ph->capacity = newCapacity;
	}

	ph->a[ph->size] = x;
	ph->size++;

	adjustUp(ph->a, ph->size - 1);
}

在堆中插入数据的前提是不改变堆的性质，使其还是一个堆，所以我们可以在最后一个位置处插入数据，再调用向上调整函数来实现插入，当然与顺序表相同的是，当容量不够时我们要进行扩容操作。

6.向下调整算法

void adjustDown(hpDataType* a, int size, int parent)
{
	int child = parent * 2 + 1;
	//调整到没有孩子结点
	while (child < size)
	{
		if (child + 1 < size && a[child + 1] < a[child])
		{
			child++;
		}
		if (a[child] < a[parent])
		{
			swap(&a[parent], & a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}	
	}
}

我们使用向下调整函数也可以实现大堆和小堆，当某一节点不存在孩子结点时，向下调整结束，由于一个父节点存在左子树和右子树，所以我们在调整时，应该判断左右子树数据的大小并且判断右子树是否存在，来决定child的位置，再比较与父节点的位置来交换父节点与孩子结点。

7.堆的删除

void hpPop(hp* ph)
{
	assert(ph);
	assert(!hpEmpty(ph));

	swap(&ph->a[ph->size - 1], &ph->a[0]);
	ph->size--;
	adjustDown(ph->a, ph->size, 0);
}

堆中数据的删除实际上指的是将堆顶数据进行删除，我们要进行的操作是将堆中最后一个数与堆顶元素互换，然后将堆的数据个数减一，这样就删除了堆顶元素，但是此时可能改变了堆的结构，我们再使用向下调整算法，调整根节点就能恢复了。

8.判空

bool hpEmpty(hp* ph)
{
	assert(ph);
	return ph->size == 0;
}

9.取堆顶数据

hpDataType hpTop(hp* ph)
{
	assert(ph);
	assert(!hpEmpty(ph));
	return ph->a[0];
}

10.打印堆中数据

void hpPrint(hp* hp)
{
	for (int i = 0; i < hp->size; ++i)
	{
		printf("%d ", hp->a[i]);
	}
	printf("\n");
}

源码

heap.h

#include<stdlib.h>
#include<stdbool.h>
#include<time.h>
typedef int hpDataType;
typedef struct heap
{
	hpDataType* a;
	int size;
	int capacity;
}hp;
void adjustUp(hpDataType* a, int child);
void adjustDown(hpDataType* a, int size, int child);

void swap(int* px, int* py);
void hpInit(hp* ph);
void hpDestory(hp* ph);
void hpPush(hp* ph, hpDataType x);
void hpPop(hp* ph);
bool hpEmpty(hp* ph);
void hpPrint(hp* ph);
hpDataType hpTop(hp* ph);

heap.c

#define _CRT_SECURE_NO_WARNINGS 1
#include"heap.h"
void swap(int* px, int* py)
{
	int tmp = *px;
	*px = *py;
	*py = tmp;
}
void adjustUp(hpDataType* a, int child)
{
	int parent = (child - 1) / 2;
	//调整到孩子结点就是根节点结束
	while (child > 0)
	{
		if (a[child] > a[parent])
		{
			int tmp = a[child];
			a[child] = a[parent];
			a[parent] = tmp;

			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
void adjustDown(hpDataType* a, int size, int parent)
{
	int child = parent * 2 + 1;
	//调整到没有孩子结点
	while (child < size)
	{
		if (child + 1 < size && a[child + 1] < a[child])
		{
			child++;
		}
		if (a[child] < a[parent])
		{
			swap(&a[parent], & a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}	
	}
}
void hpInit(hp* ph)
{
	assert(ph);
	ph->a = NULL;
	ph->capacity = ph->size = 0;
}
void hpDestory(hp* ph)
{
	assert(ph);
	free(ph->a);
	ph->a = NULL;
	ph->capacity = ph->size = 0;
}

void hpPush(hp* ph, hpDataType x)
{
	assert(ph);
	if (ph->size == ph->capacity)
	{
		hpDataType newCapacity = ph->capacity == 0 ? 4 : ph->capacity * 2;
		hpDataType* tmp = (hpDataType*)realloc(ph->a, sizeof(hpDataType)*newCapacity);
		if (tmp == NULL)
		{
			perror("realloc fail/n");
			exit(-1);
		}

		ph->a = tmp;
		ph->capacity = newCapacity;
	}

	ph->a[ph->size] = x;
	ph->size++;

	adjustUp(ph->a, ph->size - 1);
}
void hpPop(hp* ph)
{
	assert(ph);
	assert(!hpEmpty(ph));

	swap(&ph->a[ph->size - 1], &ph->a[0]);
	ph->size--;
	adjustDown(ph->a, ph->size, 0);
	
}
bool hpEmpty(hp* ph)
{
	assert(ph);
	return ph->size == 0;
}
void hpPrint(hp* hp)
{
	for (int i = 0; i < hp->size; ++i)
	{
		printf("%d ", hp->a[i]);
	}
	printf("\n");
}
hpDataType hpTop(hp* ph)
{
	assert(ph);
	assert(!hpEmpty(ph));
	return ph->a[0];
}

test.c

#define _CRT_SECURE_NO_WARNINGS 1
#include"heap.h"

void test()
{
	hp h;
	hpInit(&h);
	int a[] = { 70, 56, 30, 25, 15, 10, 1 };
	for (int i = 0; i < sizeof(a) / sizeof(a[0]); ++i)
	{
		hpPush(&h, a[i]);
	}
	hpPrint(&h);
	hpDestory(&h);
}
int main()
{
	test();
	//testTopk();
	return;
}