这里写目录标题
- 一、刷题统计(ceil函数返回的是等值于某最小整数的浮点值,不强制转换回int就wa,没错就连和int整数相加都wa
- 二、修剪灌木(主要应看清楚会调转方向
- 三、统计子矩阵(前缀和+滑动窗口⭐)
- 四、[积木画](https://www.lanqiao.cn/problems/2110/learning/)
- 顺子日期
- X进制减法
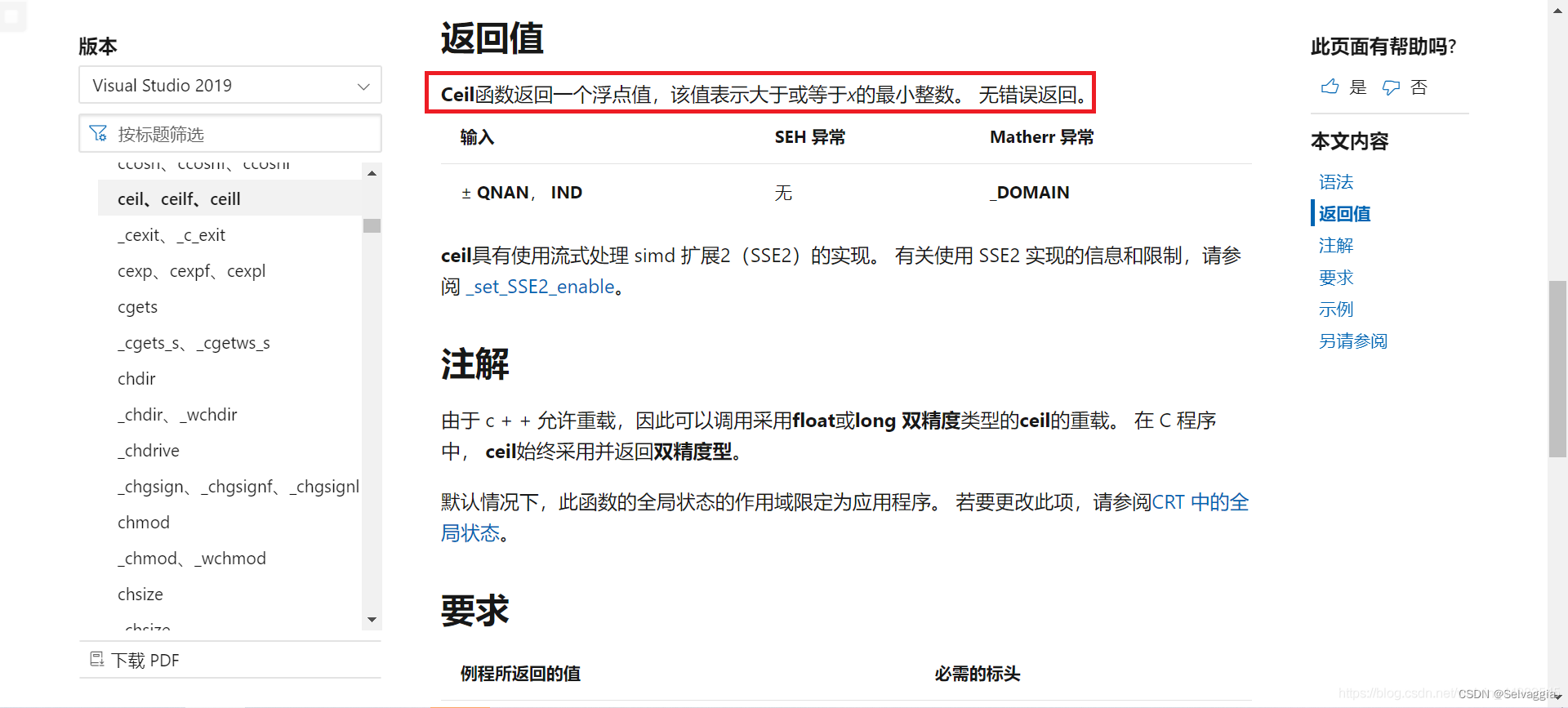
一、刷题统计(ceil函数返回的是等值于某最小整数的浮点值,不强制转换回int就wa,没错就连和int整数相加都wa

ceil函数我给你跪了,总之ceil(x) 返回的是 等值于 大于或等于x(一般为浮点数,可能是整数)的最小整数 的浮点数
#include <bits/stdc++.h>
using namespace std;
#define int long long int
signed main()
{
int res=0,sum=0;
int a,b,n;
cin>>a>>b>>n;
int x=5*a+2*b;
res+=(n/x*7);
sum+=n/x*x;
int y=n-sum;
//x=0;
//while(y>0){
// x++;
// if(x<=5)y-=a;
// else y-=b;
//}
//res+=x;
if(y>5*a){
res=res+5+(int)ceil((y-5*a)*1.0/b);
}
else res+=(int)ceil(1.0*y/a);
//if(y>5*a){
// res+=5;
// int z=((y-5*a)%b==0)?(y-5*a)/b:(y-5*a)/b+1;
// res+=z;
//}
//else{
// int z=((y%a)==0)?y/a:y/a+1;
// res+=z;
//}
cout<<res;
return 0;
}
二、修剪灌木(主要应看清楚会调转方向
#include <bits/stdc++.h>
using namespace std;
#define int long long int
int n;
const int N=10000;
int a[N];
int b[N];
signed main(){
//在第一天的 早晨, 所有灌木的高度都是 0 厘米 每天从早上到傍晩会长高 1 厘米
//当修剪了最右侧的灌木后, 她会调转方向
cin>>n;
for(int i=1;i<=n;i++){
a[i]=2*max(n-i,i-1);
cout<<a[i]<<endl;
} //3 4 5
// 1 1 1 0 1 1
// 1 2 2 1 0 2
// 2 1 3 2 1 0
// 3 2 1 3 0 1
// 4 1 2 0 1 2
// 1 2 3 1 0 3
// 2 1 4 2 1 0
// 首先容易发现,
// 1、最高的时候永远出现在晚上未修剪之前(马上要修剪了),轮流变成0
// 2、灌木的最高长度应该是对称的(调转方向)
// 3、因为有最高高度,这应该是个循环的固定模式,即每个灌木都是从0->max 重复
// 固定模式的哪个时刻出现最高高度呢?
// 刚把a[x]砍到0后,向左(或向右)走到底a[n],再往回走到a[x]的时候
return 0;
}
三、统计子矩阵(前缀和+滑动窗口⭐)
结错婚是惨过输钱,看错题惨过。。。 是不超过k不是等于k啊大佬
#include <bits/stdc++.h>
using namespace std;
#define int long long int
int n,m,k;
const int N=1005;
int a[N][N];
int b[N][N];//b[i][j],第i列 前j行的前缀和
int res=0;
void fun(int x,int y){
int s[N];
int sum[N];
memset(s,sizeof(s),0);
memset(sum,sizeof(sum),0);
for(int i=1;i<=n;i++){
s[i]=b[i][y]-b[i][x-1];
sum[i]=sum[i-1]+s[i];
}
//这里是暴力枚举区间,在双重循环下暴力导致超时
//用滑动窗口(maybe)
// for(int l=1;l<=n;l++){
// for(int r=l;r<=n;r++){
// if((sum[r]-sum[l-1])<=k)res++;
// }
// }
int l=1,r=1;
for(int r=l;r<=n;r++){
while(sum[r]-sum[l-1]>k){
l++;
}
res+=r-l+1;
//此时sum[r]-sum[l-1]<=k,由于枚举的是右端点,以r为右端点,有r-l+1个空间满足条件
}
// l l+1 l+2 l+3 (l,l+3) (l+1,l+3) (l+2,l+3) (l+3,l+3)
}
void fun1(int i,int ii){
// 这里a[i][j]是第j列前i行的前缀和
//我的题解b[i][j]是第i列前j行的前缀和
int l = 1, r = 1;//滑动窗口的左右端点
int sum = 0;//区间前缀和:[l,r]区间的累计和
for(r = 1; r <= n; r++)//遍历右端点,根据区间和调整左端点
{
sum += a[ii][r] - a[i-1][r];//加上右端点处的和
while(sum > k)//区间和了,左端点右移,区间变小
{
sum -= a[ii][l] - a[i-1][l];//减去移出去的左端点处的和
l++;
}
res += r - l + 1;//方法数就是找到的区间大小累加
}
}
signed main(){
cin>>m>>n>>k;
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
cin>>a[i][j];
b[j][i]=b[j][i-1]+a[i][j];
}
}
// 子矩阵的和
// for(int i=1;i<=n;i++){
// for(int j=1;j<=m;j++){
// cout<<b[i][j]<<" ";
// }
// cout<<endl;
// }
for(int i=1;i<=m;i++){
for(int j=i;j<=m;j++){
fun(i,j);
}
}
cout<<res;
return 0;
}
三个样例运行超时了
#include <bits/stdc++.h>
using namespace std;
#define int long long int
int n,m,k;
const int N=1005;
int a[N][N];
int b[N][N];//b[i][j],第i列 前j行的前缀和
int res=0;
void fun(int x,int y){
int s[N];
int sum[N];
memset(s,sizeof(s),0);
memset(sum,sizeof(sum),0);
for(int i=1;i<=n;i++){
s[i]=b[i][y]-b[i][x-1];
sum[i]=sum[i-1]+s[i];
}
for(int i=1;i<=n;i++){
for(int j=i;j<=n;j++){
if((sum[j]-sum[i-1])<=k)res++;
}
}
}
signed main(){
cin>>m>>n>>k;
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
cin>>a[i][j];
b[j][i]=b[j][i-1]+a[i][j];
}
}
// 子矩阵的和
// for(int i=1;i<=n;i++){
// for(int j=1;j<=m;j++){
// cout<<b[i][j]<<" ";
// }
// cout<<endl;
// }
for(int i=1;i<=m;i++){
for(int j=i;j<=m;j++){
fun(i,j);
}
}
cout<<res;
return 0;
}
四、积木画

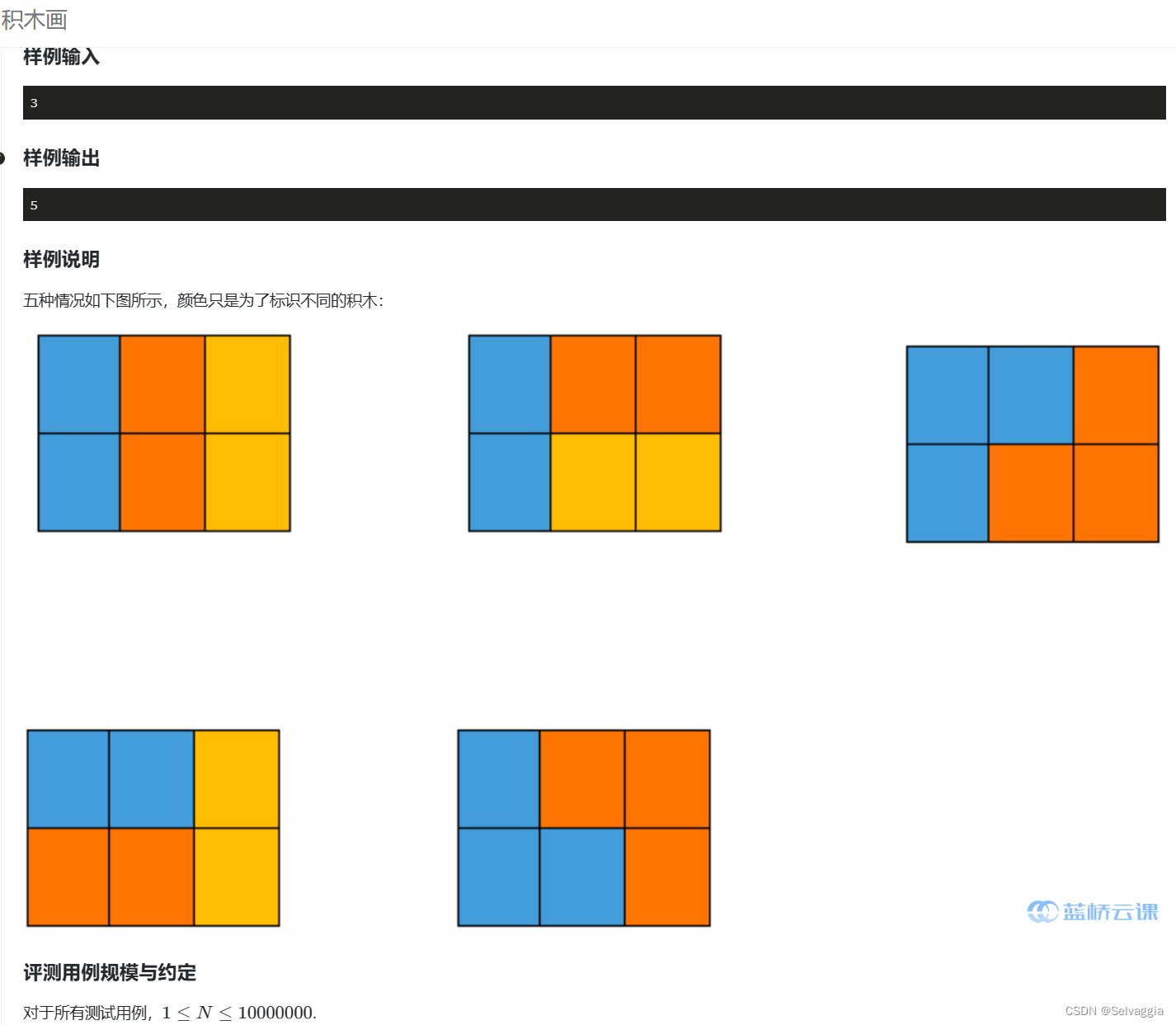
我一直以为我是对的来着(0%通过率,excuse me?呜呜呜)
fine,我看完n=3的情况下意识地以为 组合情况 要么 长方形单独拼,L形单独拼,或者是 长方形和L形混拼(而且下意识觉得两种混拼的形式只有n=3情况中枚举的这么几种),但显然简单化了(稍微动脑想想,n=5,一个L形两个长方形,这种组合情况就超出了n=3枚举的那些情况
#include <bits/stdc++.h>
using namespace std;
#define int long long int
int n,m,k;
const int mod=1000000007;
const int N=10000005;
int dp[N];
signed main(){
cin>>n;
dp[1]=1;
dp[2]=2;
dp[3]=5;
for(int i=4;i<=n;i++){
dp[i]=(dp[i-1]*1%mod+dp[i-2]*2%mod+dp[i-3]*5%mod)%mod;
}
cout<<dp[n];
return 0;
}
递归还是讲究一个状态转移,那么对于第 i i i 列可能会有哪几种情况呢?

(,阴影部分表示第
i
−
1
i-1
i−1 列已经拼好的状态,由于长方形和L形都只占两列,只需要观察第
i
−
1
i-1
i−1 列和第
i
i
i 列)
最后所求的方案数 等值于
d
p
[
n
]
[
4
]
dp[n][4]
dp[n][4]
不用担心除了第n列之外的列上下没有被覆盖满,因为看我们的状态转移图,转移方式无一不会使得第
i
−
1
i-1
i−1 列存在未被覆盖的情况,由此拼图方式递推,推到第
i
i
i 列时,不管第
i
i
i 列状态咋样,第
i
−
1
i-1
i−1 列一定被覆盖满了
正当我以为我要AC的时候,没有一声不好意思,竟让我崩溃至此
当需要开很大的数组(这里高达
1
e
7
1e7
1e7 ),尽量不要开longlong,实在不行将中途结果用强制转化成longlong的方法防止爆int,其次就是空间本来就已经不够了,数组下标还是不要作妖从1开始,从0开始节省一点

这里给256M
一、数组太大,超内存
#define int long long int
const int N=10000005;
int dp[N][5];
vector<vector<int>> dp(n + 1, vector<int>(5));
数开八位的真敢啊你,清一色的runerror,以后超过六位数就用vector(等等, 不对,vector似乎更占空间,看这题最后的一块题解,同样不开long long,vector反而不行了,这里能过30%不过是因为是根据n的大小针对性开的,有部分测试样例n比较小
二、初始化
没错的,都是内存的错
dp[1][4]=1;
dp[1][0]=1;
但为什么这个能过35%
即便避开了上面两个任意让人过%0的点,也只有勉强的30%
#include <bits/stdc++.h>
using namespace std;
#define int long long int
int n,m,k;
const int mod=1000000007;
// const int N=10000005;
// int dp[N][5];
signed main(){
cin>>n;
vector<vector<int>> dp(n + 1, vector<int>(5));
// dp[1][4]=1;
// dp[1][0]=1;
dp[0][4] = 1;
for(int i=1;i<=n;i++){
dp[i][1]=(dp[i-1][4])%mod;
dp[i][2]=(dp[i-1][1]+dp[i-1][3])%mod;
dp[i][3]=(dp[i-1][1]+dp[i-1][2])%mod;
dp[i][4]=(dp[i-1][4]+dp[i-1][3]+dp[i-1][2]+dp[i-1][1])%mod;
}
cout<<dp[n][4];
return 0;
}
AC代码 人已疯,仍然不知道在数组越界的情况下是怎么AC的,都要怀疑自己二维数组的表示一直以来是错的了
#include <bits/stdc++.h>
using namespace std;
#define LL long long int
int n,m,k;
const int mod=1000000007;
const int N=10000005;
LL dp[N][3];//改成4 变 35%,。全是超过内存限制
signed main(){
cin>>n;
// vector<vector<LL>> dp(n + 1, vector<LL>(4));这种数组声明 30% 运行错误or超内存
//忘记LL直接0%,二维长度改成3 全军覆没0%,运行错误(数组越界
//难道两种数组声明二维长度的含义不同?
dp[0][3] = 1;
for (int i = 1; i <= n; i++) {
dp[i][0] = dp[i - 1][3];
dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % mod;
dp[i][2] = (dp[i - 1][0] + dp[i - 1][1]) % mod;
dp[i][3] = (dp[i - 1][0] + dp[i - 1][1] + dp[i - 1][2] + dp[i - 1][3]) % mod;
}
cout<< dp[n][3];
return 0;
}
如果要是开long long 的dp,则会因为空间太大,错误。要是开int的dp数组,又会因为数据类型不够大,在多个int数据相加时,会超出int的范围,导致答案错误…
真正的解决办法
当需要开很大的数组(这里高达 1 e 8 1e8 1e8 ),尽量不要开longlong,实在不行将中途结果用强制转化成longlong的方法防止爆int,其次就是空间本来就已经不够了,数组下标还是不要作妖从1开始,从0开始节省一点
两种初始化方法都行
dp[1][0] = 1;
dp[1][1] = 0;
dp[1][2] = 0;
dp[1][3] = 1;
for(int i=2;i<=n;i++){
dp[0][3] = 1;
for(int i=1;i<=n;i++){
#include <bits/stdc++.h>
using namespace std;
#define ll long long int
int n,m,k;
const int mod=1000000007;
const int N=10000005;
int dp[N][4];
signed main(){
cin>>n;
// vector<vector<int>> dp(n + 1, vector<int>(4));
// dp[1][3]=1;
// dp[1][0]=1;
dp[0][3] = 1;
for(int i=1;i<=n;i++){
dp[i][0]=((ll)dp[i-1][3])%mod;
dp[i][1]=((ll)dp[i-1][0]+(ll)dp[i-1][2])%mod;
dp[i][2]=((ll)dp[i-1][0]+(ll)dp[i-1][1])%mod;
dp[i][3]=((ll)dp[i-1][3]+(ll)dp[i-1][2]+(ll)dp[i-1][1]+(ll)dp[i-1][0])%mod;
}
cout<<dp[n][3];
return 0;
}
问题又来了,即使不开 longlong数组,这里用vector声明二维数组的时候又只能过35%,我不理解

力扣原题-动态规划解释
找规律解释(类似这种的动态规划找方法数都有规律?)
顺子日期
#include <iostream>
using namespace std;
int a[10];
int mon[15]={0,31,28,31,30,31,30,31,31,30,31,30,31};
bool ok(int x){
int y=x/10000;
int m=(x%10000)/100;
int d=x%100;
if(m<1||m>12)return false;
if(d<1)return false;
if(d>mon[m])return false;
return true;
}
int main()
{
int res=0;
for(int i=20220101;i<=20221231;i++){
if(!ok(i))continue;
int cnt=0;
int x=i;
while(x){
a[cnt++]=x%10;
x/=10;
}//翻转了,判断是否 321
for(int j=0;j<6;j++){
if(a[j+1]==a[j]-1&&a[j+2]==a[j]-2){
res++;
break;
}
}
}
cout<<res;
return 0;
}
X进制减法

样例输入
11
3
10 4 0
3
1 2 0
样例输出
94


首先是找规律,第
i
i
i 位的权重是累乘
1
1
1 ~
i
−
1
i-1
i−1 的所有进制
最小的差值,我下意识以为要暴力搜索所有权值的组合情况,因为毕竟虽然
A
>
=
B
A>=B
A>=B ,难免可能统一位上
A
[
i
]
<
B
[
i
]
A[i]<B[i]
A[i]<B[i]
但也许是贪心思想,每一位都取最低的权值,就能得到最小的差值
暴力搜索版(过了30%,剩下的超时了)
#include <bits/stdc++.h>
using namespace std;
#define ll long long int
const int mod=1000000007;
const int N=100005;
int n,x,y;
int a[N],b[N],c[N];
ll res=0x3f3f3f3f;
int X[N];
void dfs(int u){
if(u==x+1){
ll tmp=a[1];
ll base=1;
for(int i=2;i<=x;i++){
base=base*X[i-1]%mod;
tmp=(tmp+a[i]*base)%mod;
}
res=min(tmp,res);
return ;
}
for(int i=2;i<=n;i++){
if(i>=c[u]){
X[u]=i;
dfs(u+1);
}
}
}
signed main(){
scanf("%d",&n);
scanf("%d",&x);
for(int i=x;i>=1;i--)scanf("%d",&a[i]);
scanf("%d",&y);
for(int i=y;i>=1;i--)scanf("%d",&b[i]);
// 最小的差
// 既然A>=B ,那么x一定大于等于y
// 每一数位上的数 字要小于其进制
for(int i=1;i<=x;i++){
c[i]=max(a[i],b[i])+1;//进制大于等于c[i]
a[i]=a[i]-b[i];
if(c[i]<2)c[i]=2;
}
dfs(1);
cout<<res;
return 0;
}
贪心AC版
解释一
因为每一位进制都会 乘到 A 和 B里面,当 base 越大的时候 A 和 B都会越大,但是因为 A >= B 的,所以 A 的增长速率是始终大于 B 的, 所以 base越大,A - B 的差值就越大,所以我们只要每次取 base 最小,就能满足 A - B 的差值最小了,又因为每一位的值都是由前面每一位的进制乘起来的
解释二
借位思想,极限思维, 一旦碰到
A
[
i
]
<
B
[
i
]
A[i]<B[i]
A[i]<B[i]就向高位借位,由于
A
>
=
B
A>=B
A>=B,最后一定可以使得 每个位置都有
A
[
i
]
>
=
B
[
i
]
A[i]>=B[i]
A[i]>=B[i]
解释三
秦九韶算法
#include <bits/stdc++.h>
using namespace std;
#define ll long long int
const int mod=1000000007;
const int N=100005;
int n,x,y;
int a[N],b[N],c[N];
ll res=0;
signed main(){
scanf("%d",&n);
scanf("%d",&x);
for(int i=x;i>=1;i--)scanf("%d",&a[i]);
scanf("%d",&y);
for(int i=y;i>=1;i--)scanf("%d",&b[i]);
// 最小的差
// 既然A>=B ,那么x一定大于等于y
// 每一数位上的数 字要小于其进制
ll base=1;
for(int i=1;i<=x;i++){
c[i]=max(a[i],b[i])+1;//进制大于等于c[i]
a[i]=a[i]-b[i];//不要改变了a[i]的含义又去用原a[i]的值 不要交换两句顺序
if(c[i]<2)c[i]=2;
res=(res+a[i]*base)%mod;
base=base*c[i]%mod;
}
cout<<res;
return 0;
}