回溯算法是一种暴力的搜索方式；回溯法一般与递归同时存在。

回溯法，一般可以解决如下几种问题：

• 组合问题：N个数里面按一定规则找出k个数的集合
• 切割问题：一个字符串按一定规则有几种切割方式
• 子集问题：一个N个数的集合里有多少符合条件的子集
• 排列问题：N个数按一定规则全排列，有几种排列方式
• 棋盘问题：N皇后，解数独等；

回溯法解决的问题都可以抽象为树形结构。因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度，都构成的树的深度。

集合的大小确定了树的宽度，递归的深度构成了树的深度。

 

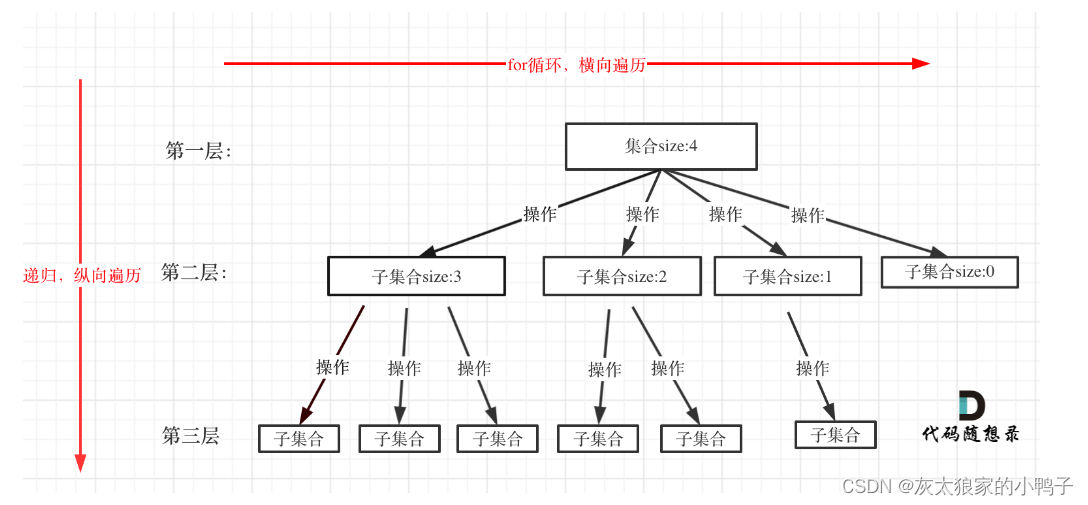
回溯算法的模板：

类似于递归三部曲：

参数（一般函数的返回值是void）、终止条件、单层递归的条件；

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}