轮盘赌选择原理

轮盘赌选择法（roulette wheel selection）是最简单也是最常用的选择方法，在该方法中，各个个体的选择概率和其适应度值成比例，适应度越大，选中概率也越大。

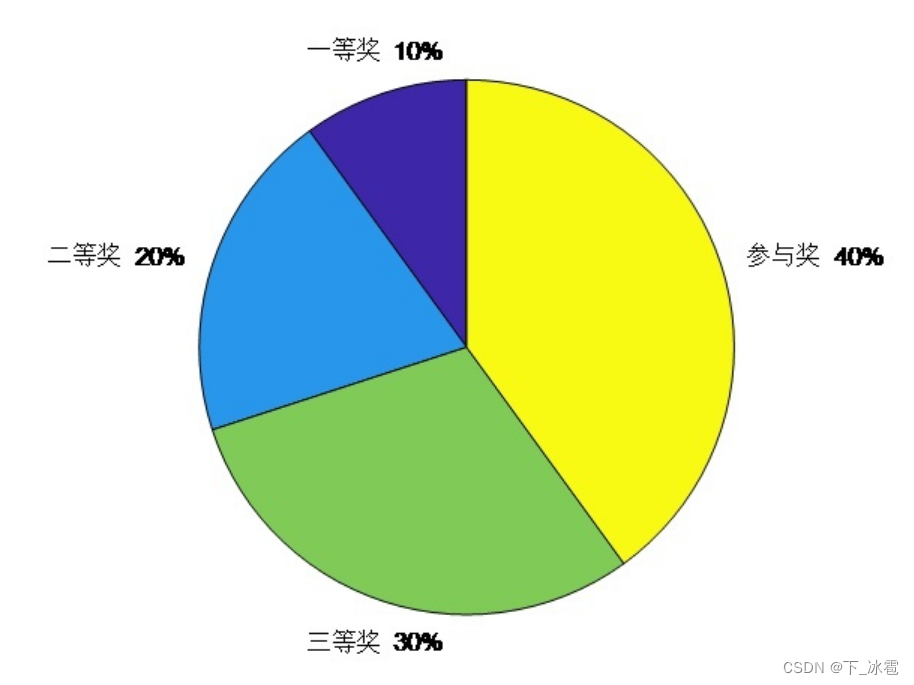
从图中可以看出一等奖、二等奖、三等奖和四等奖的概率分别为10%、20%、30%、40%，和为100%。

个体	0	1	2	3
概率	0.1	0.2	0.3	0.4

python代码实现如下：

import numpy as np

# 轮盘赌选择，list1为 list []
def roulette1(list1):
    # 产生 [0, 1) 的随机数
    r = np.random.rand()
    s = 0
    for i, v in enumerate(list1):
        s += v
        if s > r:
        	# 返回个体索引{0，1，2，3}
            return i
    return len(list1) - 1

我们测试一下roulette1，测试代码如下：

from unittest import TestCase

class Test(TestCase):
    def test_roulette1(self):
        l1 = [0.1, 0.2, 0.3, 0.4]
        result1 = [0, 0, 0, 0]
        # 执行1000次，记录每个个体的选择结果
        for i in range(1000):
            index = roulette1(l1)
            result1[index] += 1
        print('result1 =', result1)

result1 = [109, 198, 304, 389]

可以看出比例接近{0.1，0.2，0.3，0.4}。

但是对于和不为100%的情况该怎么办呢？可以将每个个体的概率进行归一化处理，即每个个体的概率除以概率之和。这样做其实比较麻烦。

也可以采用另一种方法。即在取随机数的时候不取 [0,1)的随机数，而是取 [0, s) 的随机数，s为所有个体概率之和，比如每个个体概率如下表所示：

个体	0	1	2	3
概率	0.05	0.01	0.15	0.2

所有个体概率之和为0.5，在计算时只需要取[0，0.5)的随机数即可。
python代码如下：

import numpy as np

def roulette2(list1):
    # 产生 [0, sum(list1)) 的随机数
    r = np.random.uniform(0, np.sum(list1))
    s = 0
    for i, v in enumerate(list1):
        s += v
        if s > r:
            return i
    return len(list1) - 1

同样的，测试一下：

from unittest import TestCase

class Test(TestCase):
	def test_roulette2(self):
        l2 = [0.05, 0.1, 0.15, 0.2]
        result2 = [0, 0, 0, 0]
        # 执行1000次，记录每个个体的选择结果
        for i in range(1000):
            index = roulette2(l2)
            result2[index] += 1
        print('result2 =', result2)

result2 = [105, 201, 296, 398]

可以看出比例接近{0.1，0.2，0.3，0.4}。

那么个体的排列顺序对概率是否有影响呢？没有影响。我们可以测试一下。

from unittest import TestCase

class Test(TestCase):
    def test_roulette3(self):
    	# 将个体顺序调换
        l3 = [0.15, 0.2, 0.05, 0.1]
        result3 = [0, 0, 0, 0]
        for i in range(1000):
            index = roulette2(l3)
            result3[index] += 1
        print('result3 =', result3)