第四章 串

4.1 串的定义

4.1.1 串的相关概念

1. 串：即字符串（String）是由零个或多个字符组成的有限序列。一般记为S=‘a1a2…an’ (n>=0)

   其中S是串名，单引号（注：有的地方用双引号，如Java、C，有的地方用单引号，如Python）括起来的字符序列是串的值；ai可以是字母、数字或其他字符。

2. 串的长度：串中字符的个数 n，n = 0 时的串称为空串（用$\varnothing$表示）。

3. 子串：串中任意个连续的字符组成的子序列。

4. 主串：包含子串的串。

5. 字符在主串中的位置：字符在串中的序号。(注意：位序从1开始而不是从0开始)

6. 子串在主串中的位置：子串的第一个字符在主串中的位置 。

7. 空串 vs 空格串 M=‘’ M是空串 N=’ ’ N是由三个空格字符组成的字符串，每个空格字符占1B

8. 串 vs 线性表

   ① 串是一种特殊的线性表，数据元素之间呈线性关系

   ② 串的数据对象限定为字符集（如中文字符、英文字符、数字字符、标点字符等）

   ③ 串的基本操作，如增删改查等通常以字串为操作对象

4.1.2 串的基本操作

1. StrAssign(&T, chars)：赋值操作。把串 T 赋值为 chars。
2. StrCopy(&T, S)：复制操作。由串 S 复制得到串 T。
3. StrEmpty(S)：判空操作。若 S 为空串，则返回 TRUE，否则返回 FALSE。
4. StrLength(S)：求串长。返回串 S 中元素的个数。
5. ClearString(&S)：清空操作。将 S 清为空串。
6. DestroyString(&S)：销毁串。将串 S 销毁（回收存储空间）。
7. Concat(&T, S1, S2)：串联接。用 T 返回由 S1 和 S2 联接而成的新串 。
8. SubString(&Sub, S, pos, len)：求子串。用 Sub 返回串 S 的第 pos 个字符起长度为 len 的子串。
9. Index(S, T)：定位操作。若主串 S 中存在与串 T 值相同的子串，则返回它在主串 S 中第一次出现的位置；否则函数值为 0。
10. StrCompare(S, T)：比较操作。若 S>T，则返回值>0；若 S=T，则返回值=0；若 S<T，则返回值<0。

4.1.3 串的存储结构

1、静态数组实现（定长顺序存储）

#define MAXLEN 255     //预定义最大串长为255
typedef struct {
    char ch[MAXLEN];    // 每个分量存储一个字符
    int length;         // 串的实际长度
} SString;

2、动态数组实现（堆分配存储）

typedef struct {
    char *ch;       // 按串长分配存储区，ch指向串的基地址
    int length;     // 串的长度
} HString;
HString S;
S.ch=(char *)malloc(MAXLEN*sizeof(char));  //用完需要手动free
S.length=0;

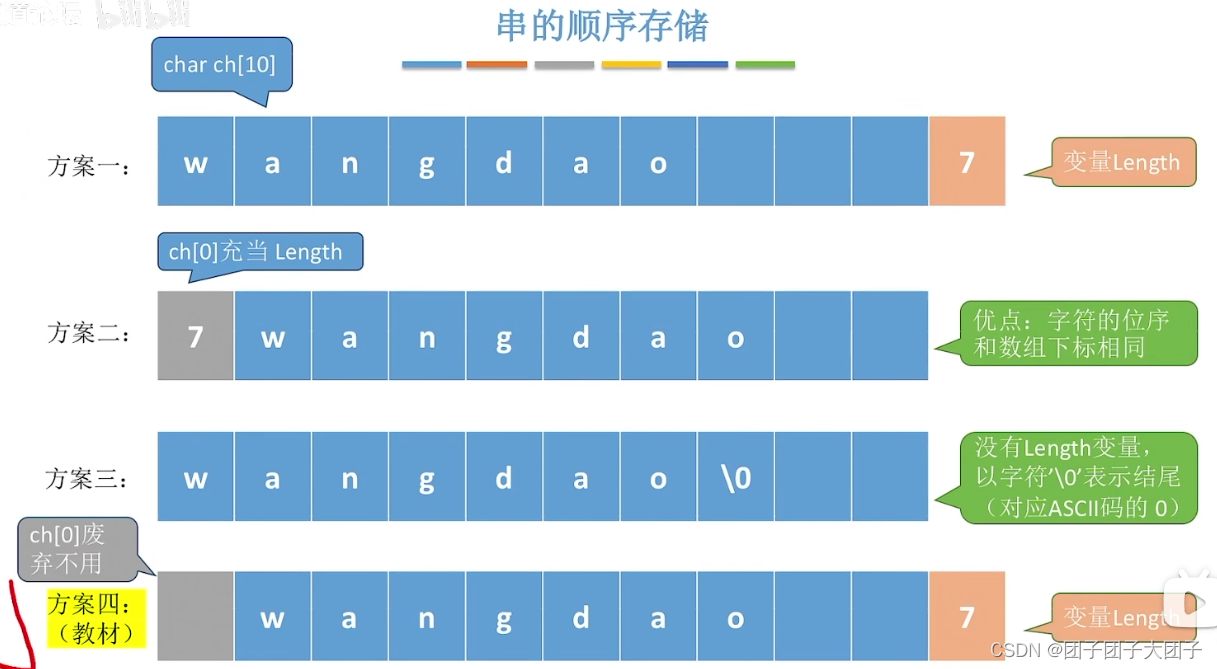
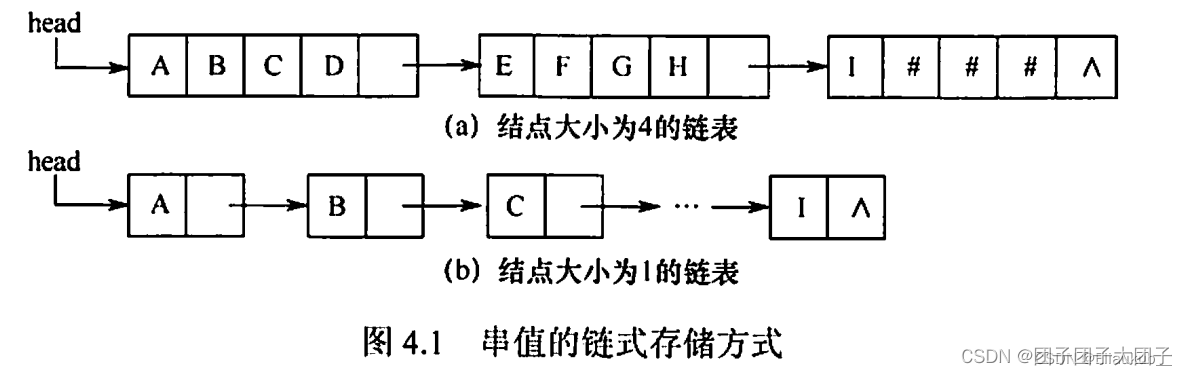
3、块链存储表示

默认情况下存储密度低，每个节点都只能存储一个字符

解决方法：一个结点存储多个字符

typedef struct StringNode{
    char ch;  //存储密度低，每个字符1B，每个指针4B
    struct StringNode * next;
}StringNode,* String;

typedef struct StringNode{
    char ch[4];
    struct StringNode *next;
}StringNode,* String;      //存储密度提高

4.2 串的模式匹配

串的模式匹配：在主串中找到与模式串相同的子串，并返回其所在位置。

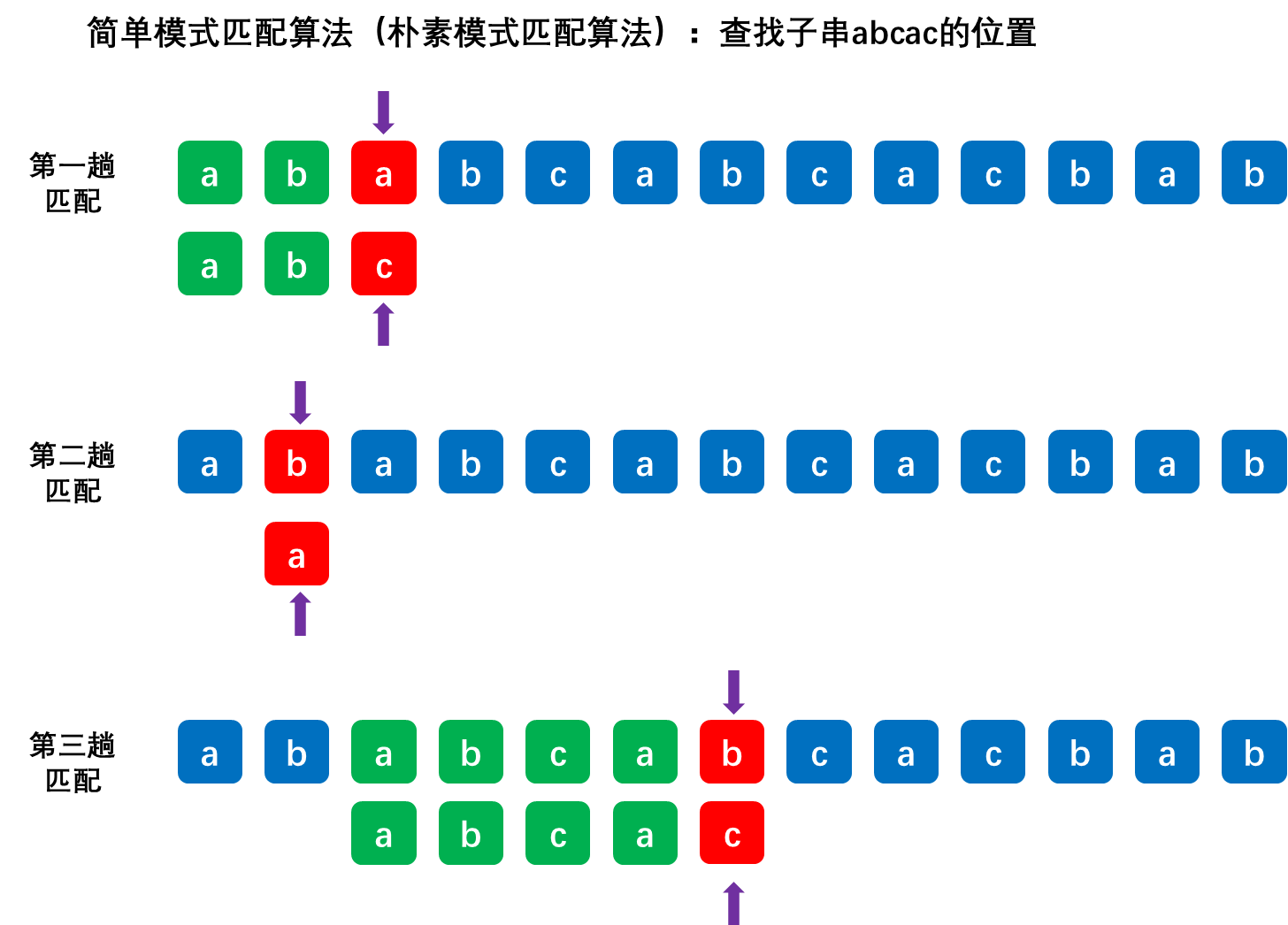
4.2.1 简单的模式匹配算法

思想：将主串中与模式串长度相同的字串拿出来，挨个与模式串对比

当子串与模式串某个对应字符不匹配时，就立即放弃当前子串，转而检索下一个子串

一个示例：

分析：

简单模式匹配算法的最坏时间复杂度是O(nm)，即每个子串都要对比到最后一个字符，如下面这种情况：

• 主串：1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2
• 子串：1 1 1 1 1 1 1 1 2

其中，n和m分别是主串和模式串的长度。

最好的情况（对于每个子串都只需对比一次）：

• 匹配成功：O(m)
• 匹配失败：O(n-m+1)=O(n-m)≈O(n)

4.2.2 KMP算法

朴素模式匹配算法的缺点：当某些子串与模式串能部分匹配时，主串的扫描指针i经常回溯，导致时间开销增加。

要了解子串的结构，首先需要了解以下几个概念：前缀、后缀和部分匹配值。

前缀：除了最后一个字符外，字符串的所有头部子串

后缀：除了第一个字符外，字符串的所有尾部子串

‘ab’的前缀是{a}，后缀是{b}，{a}∩{b}=∅，最长相等前后缀长度为0

'aba’的前缀为{a, ab}，后缀为{a, ba}, {a, ab }∩{a, ba}={a)，最长相等前后缀长度为1。

'abab '的前缀{a, ab,aba}∩后缀{b, ab, bab }={ab}，最长相等前后缀长度为2。

'ababa '的前缀{a, ab,aba, abab }∩后缀{a , ba, aba, baba }={a, aba}，公共元素有两个，最长相等前后缀长度为3。

故字符串’ababa’的部分匹配值为00123

接下来详解一下上面这个例子：

由上述方法求子串’abcac’的部分匹配值：

'ab’的前缀{a},后缀{b} {a}∩{b} = ∅

'abc’的前缀{a,ab}, 后缀{c, bc} {a,ab}∩{c, bc} = ∅

'abca’的前缀{a,ab,abc},后缀{a,ca,bca} {a,ab,abc}∩{a,ca,bca} = {a}

'abcac’的前缀{a,ab,abc,abca},后缀{c,ac,cac,bcac} {a,ab,abc}∩{c,ac,cac,bcac} = ∅

将其部分匹配值写成数组形式，就得到了部分匹配值（PM）的表：

编号	1	2	3	4	5
S	a	b	c	a	c
PM	0	0	0	1	0

接下来可以使用PM表来进行字符串匹配，其过程如下

KMP算法的原理

当c与b不匹配时，已匹配’abca’的前缀a和后缀a为最长公共元素。已知前缀a与b、c均不同，与后缀a相同，故无须比较，直接将子串移动“已匹配的字符数–对应的部分匹配值”，用子串前缀后面的元素与主串匹配失败的元素开始比较即可。

对算法的改进

已知:右移位数=已匹配的字符数-对应的部分匹配值。写成：
$$Move=(j-1)-PM[j-1]$$
现在这种情况下，我们在匹配失败时，需要去查找它前一个元素的部分匹配值，这样使用起来有点不方便，故我们可以将PM表右移一位，这样哪个元素匹配失败，则直接看它自己的部分匹配值即可。

将上例的PM表右移一位，则得到了next数组

编号	1	2	3	4	5
S	a	b	c	a	c
next	-1	0	0	0	1

我们注意到：

1）第一个元素右移以后空缺的用-1来填充，因为若是第一个元素匹配失败，则需要将子串向右移动一位，而不需要计算子串移动的位数。
2）最后一个元素在右移的过程中溢出，因为原来的子串中，最后一个元素的部分匹配值是其下一个元素使用的，但显然已没有下一个元素，故可以舍去。

这样，上式就改写为：
$$Move=(j-1)-next[j]$$
就相当于将子串的比较指针回退到：
$$j=j-Move=j-((j-1)-next[j])=next[j]+1$$
但为了让公式更加简洁，我们将next数组整体加1

next数组也可以写成:

编号	1	2	3	4	5
S	a	b	c	a	c
next	0	1	1	1	2

最终子串指针变化公式为：
$$j=next[j]$$

在实际匹配过程中，子串在内存里是不会移动的，而是指针在变化，书中画图举例只是为了让问题描述得更加形象。next[j]的含义是:在子串的第j个字符与主串发生失配时，则跳到子串的next[j]位置重新与主串当前位置进行比较。

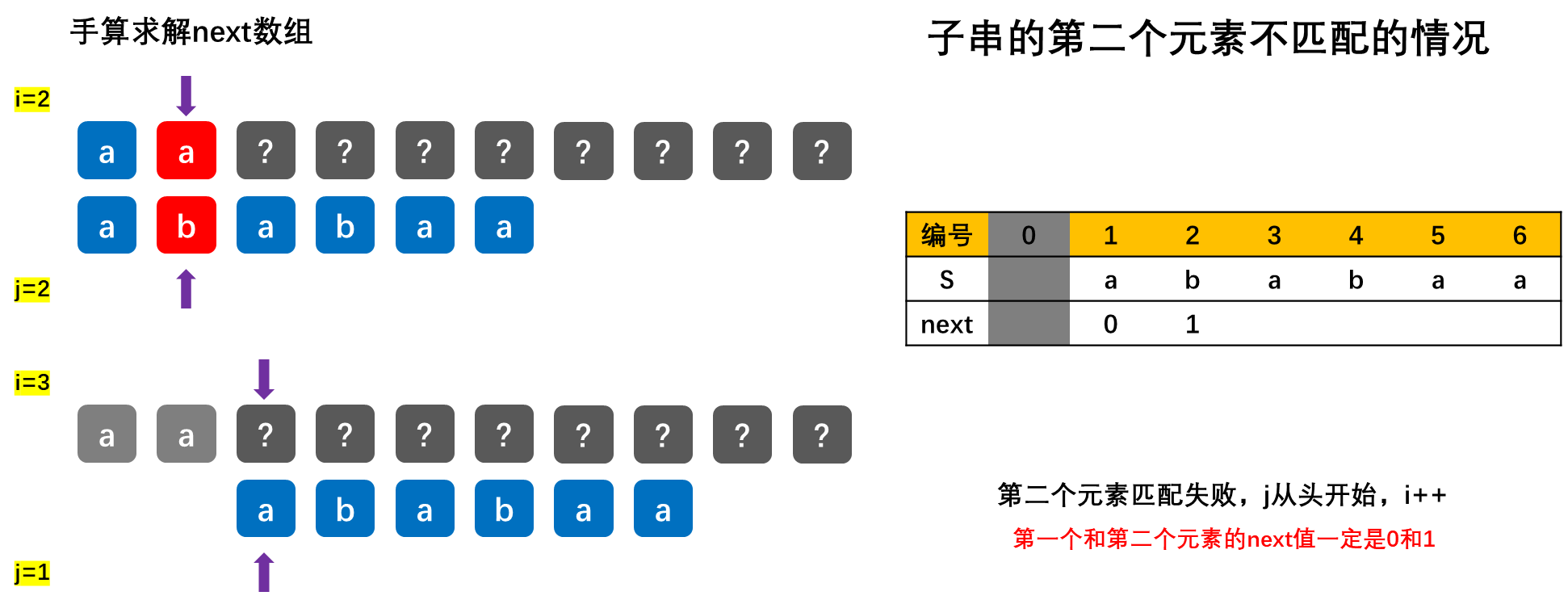
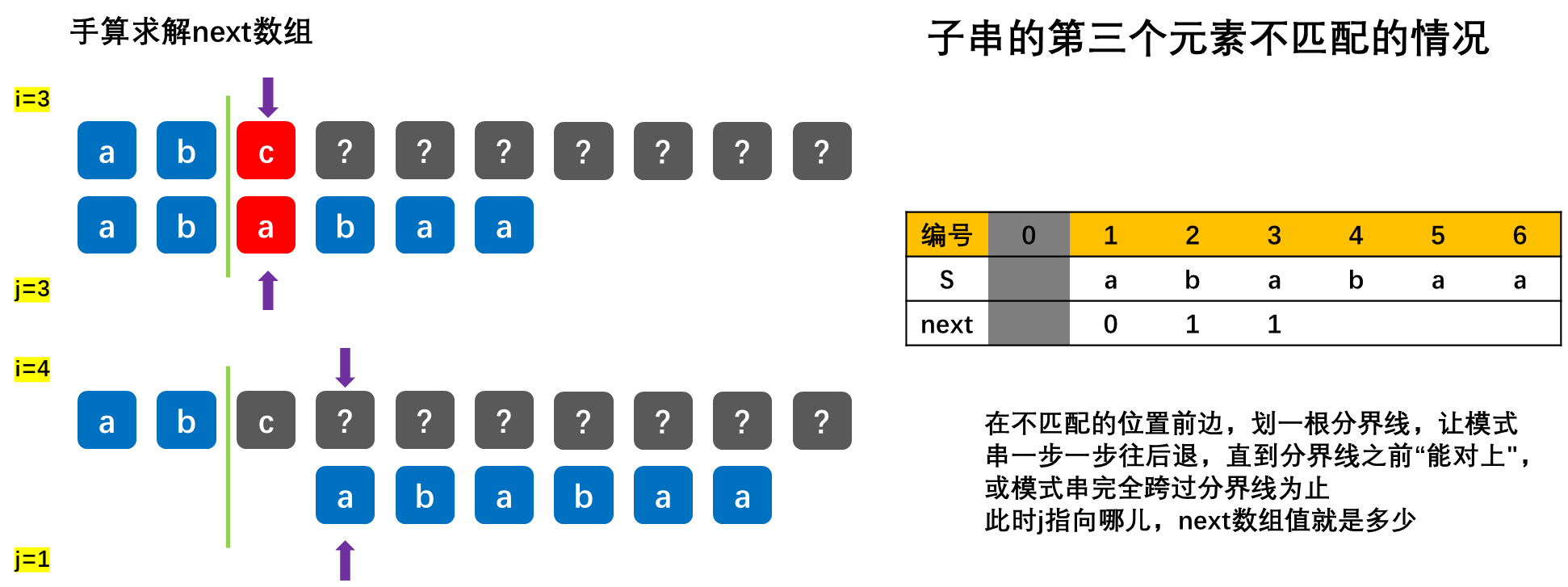
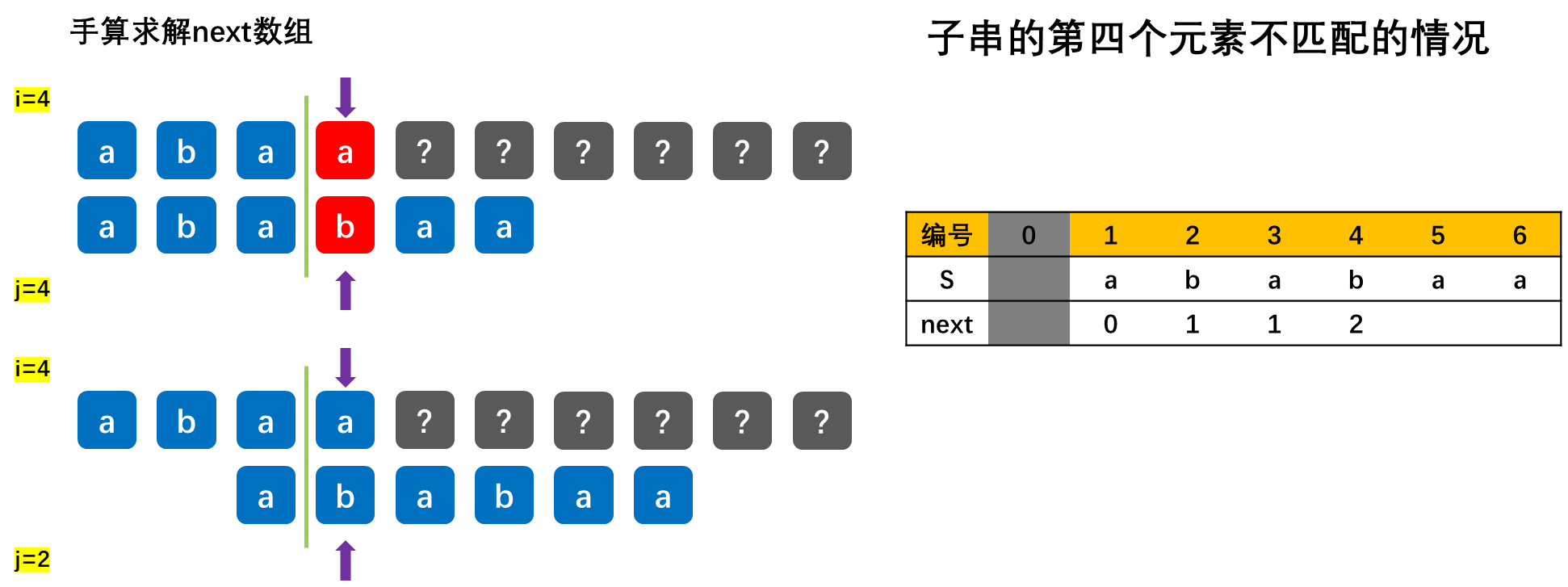
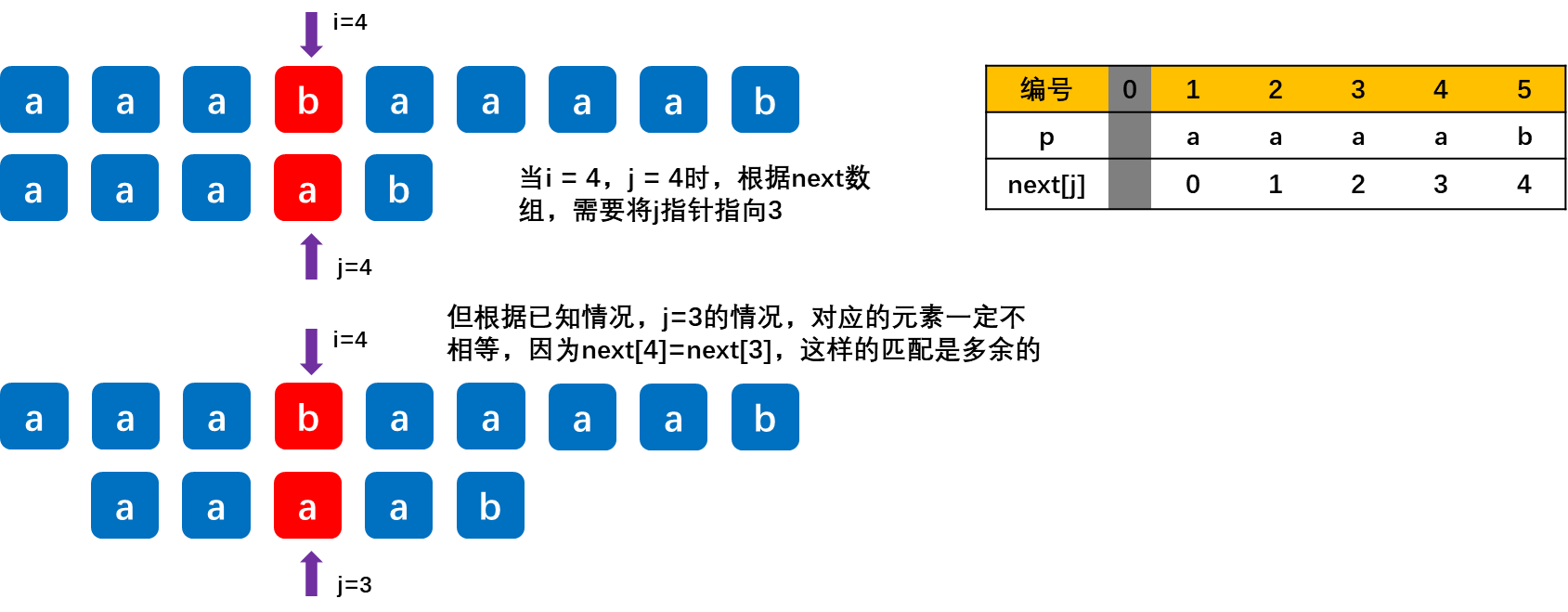
【重要】求next数组，根据如下示例来学习：

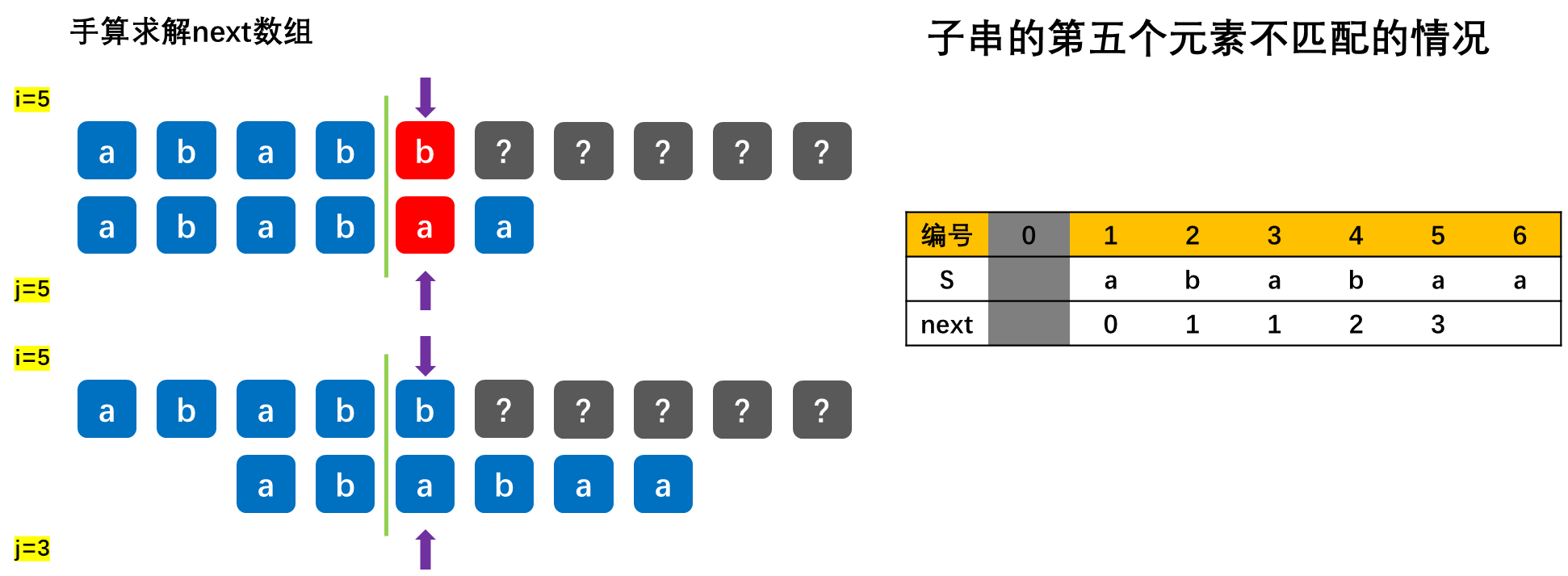
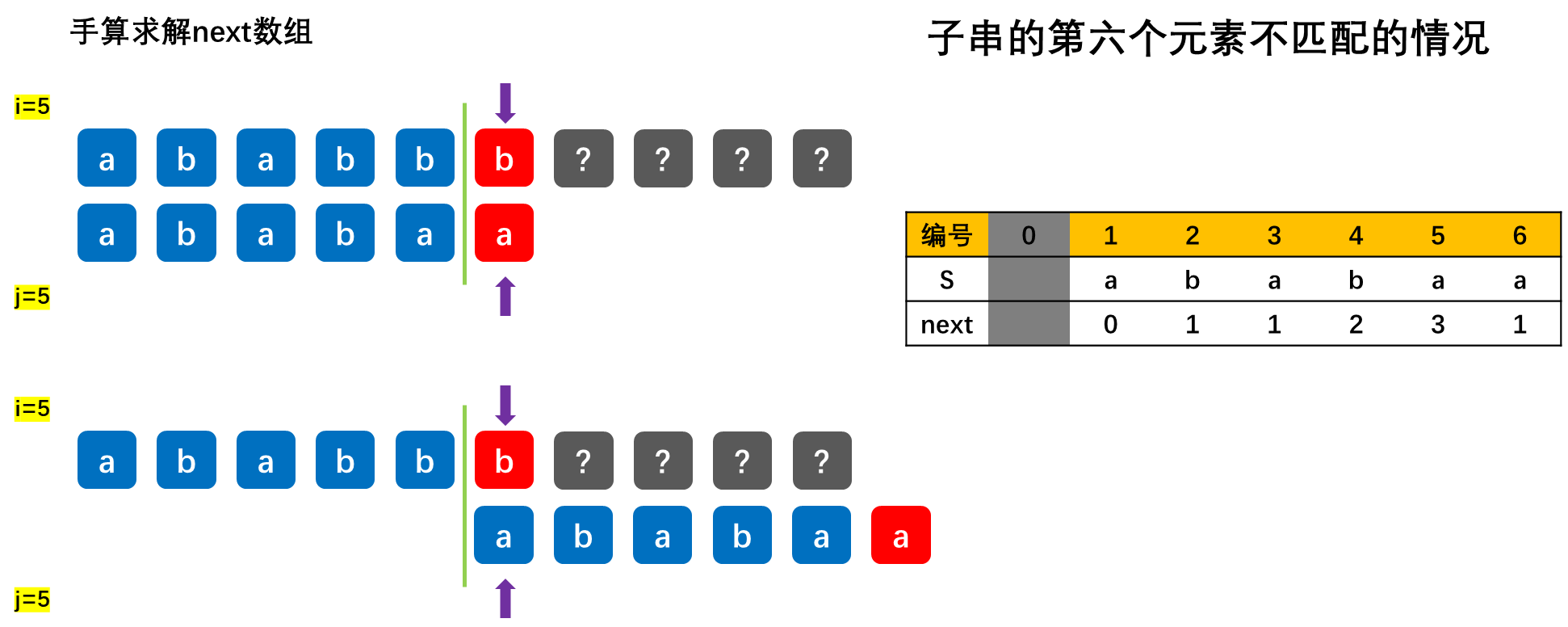
KMP算法的进一步优化

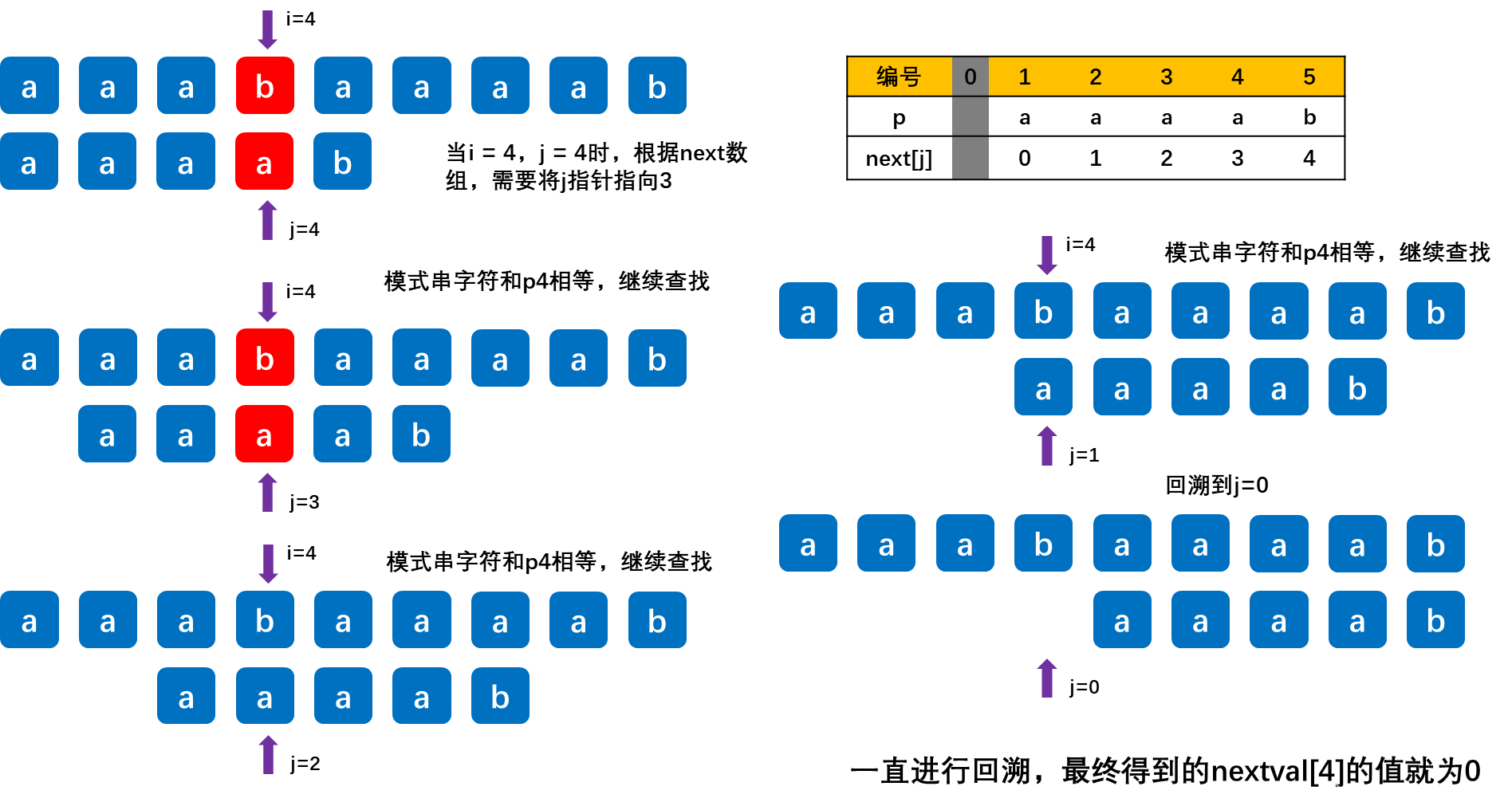
问题的产生：

所以引入了nextval数组，对KMP算法进行进一步优化。

故我们在模式串中，当前模式串p和对应的next数组p_next的模式串值相等时，继续查找对应p_next模式串的next数组对应的模式串，直到模式串对应的值不相等。

以下是匹配过程：