目录
一、填空题
(一)最小的十六进制(答案:2730)
(二)Excel的列(答案:BYT)
(三)相等日期(答案:70910)
(四)多少种取法(答案:189)
(五)最大连通分块(答案:148)
二、编程题
(一)哪一天
(二)信号覆盖
(三)清理水草
(四)最长滑行
(五)区间最小值
一、填空题
(一)最小的十六进制(答案:2730)
问题描述
请找到一个大于 2022 的最小数,这个数转换成十六进制之后,所有的数位(不含前导 0)都为字母(A 到 F)。
请将这个数的十进制形式作为答案提交。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
可以不使用变成,直接使用计算机即可.
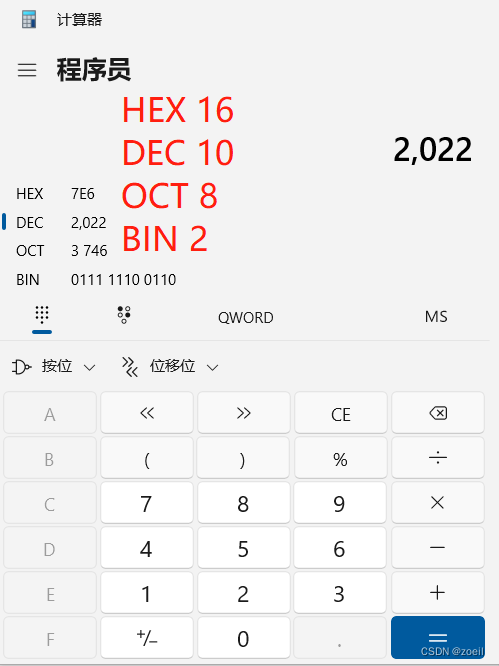
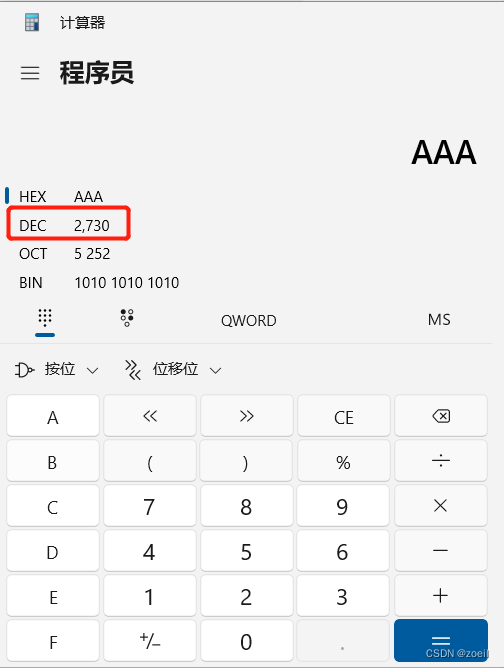
可以看到202216进制为7E6,那么要所有位数都为字母且最小,则为 AAA
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
#define fi first
#define se second
typedef long long LL;
typedef pair<int, int> PII;
string get(int x) {
string s = "";
while(x) {
int t = x % 16;
x /= 16;
if(t > 9) s += (t + 'A' - 10);
else s += (t + '0');
}
reverse(s.begin(), s.end());
return s;
}
bool check(string s) {
for(int i = 0; i < s.size(); i ++)
if(s[i] < 'A')
return false;
return true;
}
int main() {
for(int i = 2022; i ; i ++) {
string hex = get(i);
if(check(hex)) {
cout << i << endl;
break;
}
}
return 0;
}(二)Excel的列(答案:BYT)
问题描述
在 Excel 中,列的名称使用英文字母的组合。前 26 列用一个字母,依次为 A 到 Z,接下来 26*26 列使用两个字母的组合,依次为 AA 到 ZZ。
请问第 2022 列的名称是什么?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个由大写字母组成的字符串,在提交答案时只填写这个字符串,填写多余的内容将无法得分。
可以直接口算,因为26*26=676,26*26*26=17576,所以2022需要三位数表示,口算过程:
2022 % 26 = 20 == T
2022 /= 26 == 77
77 % 26 == 25 == Y
77 /= 26 == 2
2 == B
答案:BYT代码差不多的思路,这里就不写了
(三)相等日期(答案:70910)
问题描述
对于一个日期,我们可以计算出年份的各个数位上的数字之和,也可以分别计算月和日的各位数字之和。请问从 1900 年 1 月 1 日至 9999 年 12 月 31 日,总共有多少天,年份的数位数字之和等于月的数位数字之和加日的数位数字之和。
例如,2022年11月13日满足要求,因为 2+0+2+2=(1+1)+(1+3) 。
请提交满足条件的日期的总数量。这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
#define fi first
#define se second
typedef long long LL;
typedef pair<int, int> PII;
int month[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
int get(int x) {
int res = 0;
while(x) {
res += x % 10;
x /= 10;
}
return res;
}
int main() {
int ans = 0;
for(int i = 1900; i <= 9999; i ++) {
int syear = get(i);
bool is_leap = !(i % 400) || (i % 100 && !(i % 4));
for(int j = 1; j <= 12; j ++) {
if(j == 2 && is_leap) month[2] = 29;
else month[2] = 28;
for(int k = 1; k <= month[j]; k ++)
{
int smd = get(j) + get(k);
if(smd == syear) {
ans ++;
}
}
}
}
cout << ans << endl;
return 0;
}(四)多少种取法(答案:189)
问题描述
小蓝有 30 个数,分别为:99, 22, 51, 63, 72, 61, 20, 88, 40, 21, 63, 30, 11, 18, 99, 12, 93, 16, 7, 53, 64, 9, 28, 84, 34, 96, 52, 82, 51, 77 。
小蓝可以在这些数中取出两个序号不同的数,共有 30*29/2=435 种取法。
请问这 435 种取法中,有多少种取法取出的两个数的乘积大于等于 2022 。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
#define fi first
#define se second
typedef long long LL;
typedef pair<int, int> PII;
int a[] = {99, 22, 51, 63, 72, 61, 20, 88, 40, 21, 63, 30, 11, 18, 99, 12, 93, 16, 7, 53, 64, 9, 28, 84, 34, 96, 52, 82, 51, 77};
int main() {
int res = 0;
for(int i = 0; i < 30; i ++)
for(int j = i + 1; j < 30; j ++)
if(i != j && a[i] * a[j] >= 2022)
res ++;
cout << res << endl;
return 0;
}(五)最大连通分块(答案:148)
问题描述
小蓝有一个 30 行 60 列的数字矩阵,矩阵中的每个数都是 0 或 1 。
110010000011111110101001001001101010111011011011101001111110
010000000001010001101100000010010110001111100010101100011110
001011101000100011111111111010000010010101010111001000010100
101100001101011101101011011001000110111111010000000110110000
010101100100010000111000100111100110001110111101010011001011
010011011010011110111101111001001001010111110001101000100011
101001011000110100001101011000000110110110100100110111101011
101111000000101000111001100010110000100110001001000101011001
001110111010001011110000001111100001010101001110011010101110
001010101000110001011111001010111111100110000011011111101010
011111100011001110100101001011110011000101011000100111001011
011010001101011110011011111010111110010100101000110111010110
001110000111100100101110001011101010001100010111110111011011
111100001000001100010110101100111001001111100100110000001101
001110010000000111011110000011000010101000111000000110101101
100100011101011111001101001010011111110010111101000010000111
110010100110101100001101111101010011000110101100000110001010
110101101100001110000100010001001010100010110100100001000011
100100000100001101010101001101000101101000000101111110001010
101101011010101000111110110000110100000010011111111100110010
101111000100000100011000010001011111001010010001010110001010
001010001110101010000100010011101001010101101101010111100101
001111110000101100010111111100000100101010000001011101100001
101011110010000010010110000100001010011111100011011000110010
011110010100011101100101111101000001011100001011010001110011
000101000101000010010010110111000010101111001101100110011100
100011100110011111000110011001111100001110110111001001000111
111011000110001000110111011001011110010010010110101000011111
011110011110110110011011001011010000100100101010110000010011
010011110011100101010101111010001001001111101111101110011101
如果从一个标为 1 的位置可以通过上下左右走到另一个标为 1 的位置,则称两个位置连通。与某一个标为 1 的位置连通的所有位置(包括自己)组成一个连通分块。
请问矩阵中最大的连通分块有多大?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
宽搜即可
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
#define fi first
#define se second
typedef long long LL;
typedef pair<int, int> PII;
char g[35][65];
bool st[35][65];
int n = 30, m = 60;
int dx[] = {1, 0, -1, 0}, dy[] = {0, 1, 0, -1};
int bfs(int u, int v) {
int ans = 1;
st[u][v] = true;
queue<PII> q;
q.push({u, v});
while(q.size()) {
auto t = q.front();
q.pop();
for(int i = 0; i < 4; i ++) {
int x = dx[i] + t.fi, y = dy[i] + t.se;
if(x < 1 || x > n || y < 1 || y > m) continue;
if(st[x][y]) continue;
if(g[x][y] == '1') {
st[x][y] = true;
q.push({x, y});
ans ++;
}
}
}
return ans;
}
int main() {
memset(st, 0, sizeof st);
for(int i = 1; i <= 30; i ++)
for(int j = 1; j <= 60; j ++)
cin >> g[i][j];
int res = 0;
for(int i = 1; i <= 30; i ++)
for(int j = 1; j <= 60; j ++)
if(!st[i][j] && g[i][j] == '1')
{
res = max(res, bfs(i, j));
}
cout << res << endl;
return 0;
}二、编程题
(一)哪一天
问题描述
给定一天是一周中的哪天,请问 n 天后是一周中的哪天?
输入格式
输入第一行包含一个整数 w,表示给定的天是一周中的哪天,w 为 1 到 6 分别表示周一到周六,w 为 7 表示周日。
第二行包含一个整数 n。
输出格式
输出一行包含一个整数,表示 n 天后是一周中的哪天,1 到 6 分别表示周一到周六,7 表示周日。
样例输入
6
10
样例输出
2
评测用例规模与约定
对于所有评测用例,1 <= n <= 1000000。
day等于7得时需要特判一下输出7
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
#define fi first
#define se second
typedef long long LL;
typedef pair<int, int> PII;
int main() {
int day, w;
cin >> day >> w;
w %= 7;
day += w;
day %= 7;
cout << (day == 0 ? 7 : day) << endl;
return 0;
} (二)信号覆盖
问题描述
小蓝负责一块区域的信号塔安装,整块区域是一个长方形区域,建立坐标轴后,西南角坐标为 (0, 0), 东南角坐标为 (W, 0), 西北角坐标为 (0, H), 东北角坐标为 (W, H)。其中 W, H 都是整数。
他在 n 个位置设置了信号塔,每个信号塔可以覆盖以自己为圆心,半径为 R 的圆形(包括边缘)。
为了对信号覆盖的情况进行检查,小蓝打算在区域内的所有横纵坐标为整数的点进行测试,检查信号状态。其中横坐标范围为 0 到 W,纵坐标范围为 0 到 H,总共测试 (W+1) * (H+1) 个点。
给定信号塔的位置,请问这 (W+1)*(H+1) 个点中有多少个点被信号覆盖。输入第一行包含四个整数 W, H, n, R,相邻整数之间使用一个空格分隔。
接下来 n 行,每行包含两个整数 x, y,表示一个信号塔的坐标。信号塔可能重合,表示两个信号发射器装在了同一个位置。输出一行包含一个整数,表示答案。
样例输入
10 10 2 5
0 0
7 057
对于所有评测用例,1 <= W, H <= 100,1 <= n <= 100, 1 <= R <= 100, 0 <= x <= W, 0 <= y <= H。
编程题 2 枚举每个点到每个哨站的距离 10000*100 = 1e6 不会爆
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
#define fi first
#define se second
typedef long long LL;
typedef pair<int, int> PII;
int w, h, n, r;
PII p[105];
bool st[105][105];
int main() {
cin >> w >> h >> n >> r;
for(int i = 0; i < n; i ++)
{
int x, y;
scanf("%d%d", &x, &y);
p[i] = {x, y};
st[x][y] = true;
}
for(int i = 0; i <= w; i ++)
for(int j = 0; j <= h; j ++)
{
for(int k = 0; k < n; k ++) {
if(st[i][j]) break;
double dist = sqrt(abs(p[k].fi - i) * abs(p[k].fi - i) + abs(p[k].se - j) * abs(p[k].se - j) );
if(dist <= r) {
st[i][j] = true;
break;
}
}
}
int res = 0;
for(int i = 0; i <= w; i ++)
for(int j = 0; j <= h; j ++)
{
if(st[i][j]) res ++;
}
cout << res << endl;
return 0;
}(三)清理水草
问题描述
小蓝有一个 n * m 大小的矩形水域,小蓝将这个水域划分为 n 行 m 列,行数从 1 到 n 标号,列数从 1 到 m 标号。每行和每列的宽度都是单位 1 。
现在,这个水域长满了水草,小蓝要清理水草。
每次,小蓝可以清理一块矩形的区域,从第 r1 行(含)到第 r2 行(含)的第 c1 列(含)到 c2 列(含)。
经过一段时间清理后,请问还有多少地方没有被清理过。输入第一行包含两个整数 n, m,用一个空格分隔。
第二行包含一个整数 t ,表示清理的次数。
接下来 t 行,每行四个整数 r1, c1, r2, c2,相邻整数之间用一个空格分隔,表示一次清理。请注意输入的顺序。输出一行包含一个整数,表示没有被清理过的面积。
样例输入1
2 3
2
1 1 1 3
1 2 2 22
30 20
2
5 5 10 15
6 7 15 9519
对于所有评测用例,1 <= r1 <= r2 <= n <= 100, 1 <= c1 <= c2 <= m <= 100, 0 <= t <= 100。
编程题 3 二维前缀和
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
#define fi first
#define se second
typedef long long LL;
typedef pair<int, int> PII;
int n, m;
int g[105][105];
void insert(int x1, int y1, int x2, int y2) {
g[x1][y1] += 1;
g[x2 + 1][y1] -= 1;
g[x1][y2 + 1] -= 1;
g[x2 + 1][y2 + 1] += 1;
}
int main() {
int t;
cin >> n >> m >> t;
int x1, x2, y1, y2;
for(int i = 0; i < t; i ++) {
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
insert(x1, y1, x2, y2);
}
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= m; j ++)
g[i][j] += g[i - 1][j] + g[i][j - 1] - g[i - 1][j - 1];
int res = 0;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= m; j ++)
if(!g[i][j]) res ++;
cout << res << endl;
return 0;
}(四)最长滑行
问题描述
小蓝准备在一个空旷的场地里面滑行,这个场地的高度不一,小蓝用一个 n 行 m 列的矩阵来表示场地,矩阵中的数值表示场地的高度。
如果小蓝在某个位置,而他上、下、左、右中有一个位置的高度(严格)低于当前的高度,小蓝就可以滑过去,滑动距离为 1 。
如果小蓝在某个位置,而他上、下、左、右中所有位置的高度都大于等于当前的高度,小蓝的滑行就结束了。
小蓝不能滑出矩阵所表示的场地。
小蓝可以任意选择一个位置开始滑行,请问小蓝最多能滑行多远距离。
输入格式
输入第一行包含两个整数 n, m,用一个空格分隔。
接下来 n 行,每行包含 m 个整数,相邻整数之间用一个空格分隔,依次表示每个位置的高度。
输出格式
输出一行包含一个整数,表示答案。
样例输入
4 5
1 4 6 3 1
11 8 7 3 1
9 4 5 2 1
1 3 2 2 1
样例输出
7
样例说明
滑行的位置一次为 (2, 1), (2, 2), (2, 3), (3, 3), (3, 2), (4, 2), (4, 3)。
评测用例规模与约定
对于 30% 评测用例,1 <= n <= 20,1 <= m <= 20,0 <= 高度 <= 100。
对于所有评测用例,1 <= n <= 100,1 <= m <= 100,0
自己写的时候没想到记忆化搜索,对于这块知识点了解的也比较少,直接使用dfs暴力了
// 编程题 4 暴力递归
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
#define fi first
#define se second
typedef long long LL;
typedef pair<int, int> PII;
int n, m;
int g[105][105];
bool st[105][105];
int res = 0;
int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0};
void dfs(int u, int v, int cnt) {
res = max(res, cnt);
for(int i = 0; i < 4; i ++) {
int x = dx[i] + u, y = dy[i] + v;
if(x < 1 || x > n || y < 1 || y > n) continue;
if(g[x][y] <= g[u][v]) continue;
if(st[x][y]) continue;
st[x][y] = true;
dfs(x, y, cnt + 1);
st[x][y] = false;
}
}
int main() {
cin >> n >> m;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= m; j ++)
{
scanf("%d", &g[i][j]);
}
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= m; j ++)
{
st[i][j] = true;
dfs(i, j, 1);
st[i][j] = false;
}
cout << res << endl;
return 0;
}网上了解到的记忆化搜索
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
#define fi first
#define se second
typedef long long LL;
typedef pair<int, int> PII;
int n, m, res;
int g[105][105];
int dist[105][105];
int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0};
int dfs(int u, int v) {
if(dist[u][v] != -1) return dist[u][v];
dist[u][v] = 1;
for(int i = 0; i < 4; i ++) {
int x = dx[i] + u, y = dy[i] + v;
if(x < 1 || x > n || y < 1 || y > n) continue;
if(g[x][y] <= g[u][v]) continue;
dist[u][v] = max(dist[u][v], dfs(x, y) + 1);
}
return dist[u][v];
}
int main() {
cin >> n >> m;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= m; j ++)
{
scanf("%d", &g[i][j]);
}
memset(dist, -1, sizeof dist);
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= m; j ++)
{
res = max(res, dfs(i, j));
}
cout << res << endl;
return 0;
}(五)区间最小值
小蓝有一个序列a[1], a[2]. .... a[n].
给定一个正整数k,请问对于每一个1到n之间的序号i,a[i-k], a[i-k+1].... a[i+k]这2k+1个数中的最小值是多少?当某个下标超过1到n的范围时,数不存在,求最小值时只取存在的那些值。
输入格式
输入的第一行包含一整数n。
第二行包含n个整数,分别表示a[1], a[2]. ... a[n]。第三行包含一个整数k。
输出格式
输出一行,包含n个整数,分别表示对于每个序号求得的最小值。
样例输入
5
5 2 7 4 3
1
样例输出
2 2 2 3 3
评测用例规模与约定
对于30%的评测用例,1<= n<= 1000,1 <= a[i]<=1000。
对于50%的评测用例,1<= n<= 10000,1 <= a[]<=10000。
对于所有评测用例,1<= n<= 1000000,1 <= a[i]<=100000。
可转化为求每个数左边2k范围内最小的数字,使用单调队列即可
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
#define fi first
#define se second
typedef long long LL;
typedef pair<int, int> PII;
const int N = 1000005;
int a[N];
int q[N], tt = -1, hh = 0;
int main() {
int n, k;
cin >> n;
for(int i = 0; i < n; i ++) {
scanf("%d", &a[i]);
}
cin >> k;
for(int i = 0; i < n; i ++) {
while(tt >= hh && a[q[tt]] >= a[i]) tt --;
while(tt >= hh && i - q[hh] + 1 > 2 * k + 1) hh ++;
q[++ tt] = i;
if(i >= k)
printf("%d ", a[q[hh]]);
}
for(int i = 0; i < k; i ++)
printf("%d ", a[q[hh]]);
return 0;
} 赛后看到网上有使用ST表的,蒟蒻完全没学过
总结:
萌新一个,有错误或者有更好的做法请各位大佬评论区提出和讨论