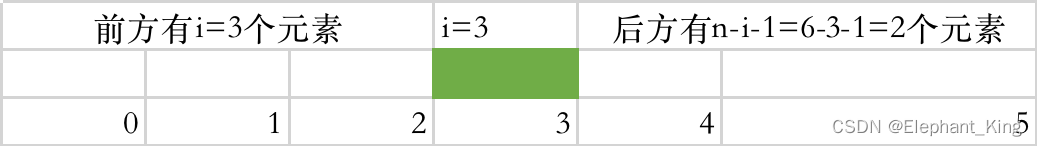个人主页：平行线也会相交
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创
收录于专栏【数据结构初阶（C实现）】

时间复杂度（就是一个函数）的计算，在算法中的基本操作的执行次数。就是算法的时间复杂度。

1

void Func1(int N)
{
	int count = 0;
	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < N; j++)
		{
			count++;
		}
	}
	for (int k = 0; k < 2 * N; k++)
	{
		count++;
	}
	int M = 10;
	while (M--)
	{
		count++;
	}
	printf("%d\n", count);
}

Func1执行的基本操作次数：F(N)=N^2+2*N+10。Func1的时间复杂度就是O（N^2）。

2

void Func2(int N)
{
	int count = 0;
	for (int k = 0; k < 2 * N; k++)
	{
		count++;
	}
	int M = 10;
	while (M--)
	{
		count++;
	}
	printf("%d\n", count);
}

Func2的时间复杂度是O(N)。

3

void Func3(int N,int M)
{
	int count = 0;
	for (int k = 0; k < M; k++)
	{
		count++;
	}
	for (int k = 0; k < N; k++)
	{
		count++;
	}
	printf("%d\n", count);
}

Func3的时间复杂度是：O(M+N)。

4

void Func4(int N)
{
	int count = 0;
	for (int k = 0; k < 100; k++)
	{
		count++;
	}
	printf("%d\n", count);
}

对于这种运行次数可以确定为常数次的时间复杂度就是O(1)。

5

const char* strchr(const char* str, int character)
{
	while (*str)
	{
		if (*str == character)
		{
			return str;
		}
		str++;
	}
}

最好情况：1次找到。
最坏情况：N次找到。
平均情况：N/2次找到。
由于在实际算法种关注的是算法最坏情况的运行情况，所以说数组中搜索数据时间复杂度为O(N)。

6

int BinarySearch(int* a, int n, int x)
{
	assert(a);
	int begin = 0;
	int end = n - 1;
	while (begin <= end)
	{
		int mid = begin + ((end - begin) >> 1);
		if (a[mid] > x)
		{
			end = mid - 1;
		}
		else if (a[mid] < x)
		{
			begin = mid + 1;
		}
		else
		{
			return mid;
		}
	}
	return -1;
}

二分查找就是用来查找你要查找的数据的，如果找到了，就返回所要查找数据的下标。
先来看一下最好情况：O（1），即查找一次就找到了。

看一下最坏情况：log以2为底，N的对数。

最好情况是1次很好理解，即把数据折半一次就找到了。
我们来看一下最坏的情况：我们首先要知道，查找一次，数据就要折半一次，查找一次，数据就要折半一次；所以当你一直查找，即一直折半直到折半到只有一个数据的时候，此时要么找到了，要么就没找到（没找到就是这些数据中根本就没有你所要查找的数据）。
比如：假设N是数组中元素的个数，x表示最坏情况的查找次数。查找一次就折半一次，即N/2，查找第二次：N/2/2；查找第三次：N/2/2/2，所以你要查找几次就需要除以几个2，直到最后查找到最后数组中只剩下一个元素的时候，即N/2/2/2/2……/2（除以x个2）=1；
把该式子整理一下就变成了这样：2^x=N，x=log以2为底N的对数。即：

7

//计算阶乘递归Fac的时间复杂度
long long Fac(size_t N)
{
	if (N == 0)
	{
		return 1;//0!=1
	}
	else
	{
		return Fac(N - 1) * N;
	}
}

时间复杂度是O（N），准确来说是O（N+1），只不过那个1忽略不计了。

8

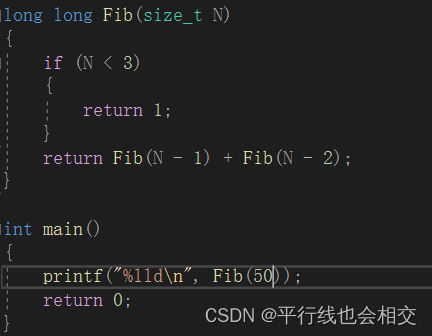
//计算斐波那契数列Fib的时间复杂度
long long Fib(size_t N)
{
	if (N < 3)
	{
		return 1;
	}
	return Fib(N - 1) + Fib(N - 2);
}

但是这个算法很慢，当N是50的时候就要运行很长时间才行。

9

void BubbleSort(int* a, int n)
{
	assert(a);
	int i = 0;
	for (i = 0; i < n-1; i++)
	{
		int j = 0;
		int count = 0;
		for (j = 0; j < n - 1 - i; j++)
		{
			if (a[j] > a[j + 1])
			{
				int tmp = a[j];
				a[j] = a[j + 1];
				a[j + 1] = tmp;
				count = 1;
			}
		}
		if (count == 0)
		{
			break;
		}
	}
}

最好情况就是冒泡排序的第一趟就好了即O(N)。
最坏情况：O(N^2)。

好了，以上就是一些时间复杂度的一些计算，就到这里吧各位。
再见啦！！！