题目链接
1049 数列的片段和
题目描述
给定一个正数数列,我们可以从中截取任意的连续的几个数,称为片段。例如,给定数列 { 0.1, 0.2, 0.3, 0.4 },我们有 (0.1) (0.1, 0.2) (0.1, 0.2, 0.3) (0.1, 0.2, 0.3, 0.4) (0.2) (0.2, 0.3) (0.2, 0.3, 0.4) (0.3) (0.3, 0.4) (0.4) 这 10 个片段。
给定正整数数列,求出全部片段包含的所有的数之和。如本例中 10 个片段总和是 0.1 + 0.3 + 0.6 + 1.0 + 0.2 + 0.5 + 0.9 + 0.3 + 0.7 + 0.4 = 5.0。
输入格式:
输入第一行给出一个不超过 10
5
的正整数 N,表示数列中数的个数,第二行给出 N 个不超过 1.0 的正数,是数列中的数,其间以一个空格分隔。
输出格式:
在一行中输出该序列所有片段包含的数之和,精确到小数点后 2 位。
输入样例:
4
0.1 0.2 0.3 0.4
输出样例:
5.00
题目大意
解题思路
首先我们看到范围,可以知道这道题暴力的话是一定会超限的,因为暴力最少要用两重for循环,对于10^5^ 这种数量级,双重for循环时间复杂度达到了10^10^这种数量级,根据经验来讲千万级别(10^7^)是比较安全的,到了亿级别(10^8^)就开始有风险了,在向上的数量级不出意外都会超限
这道题非常考验临场反应能力,其实这道题代码含量不高,但是对数学的要求是有的,想出规律以后代码是非常简单的,首先第一反应是暴力,但是范围并不允许,所以就是要找规律,我记得我第一遍做的时候也是没做出来,到后面好好想了想,想到了之前做到的这个题【全网最细PAT题解】【PAT乙】1040 有几个PAT当时的思路是以当前位置为起点,然后判断前后各有多少种情况,然后利用到本题上也是行得通的,下面来讲一下思路
思路
 假设数组长度为
假设数组长度为6,我们现在判断下标为3的这个元素,我们要做的是找到,从哪个元素开始能包括i=3这个位置的元素
- 首先从
i前面的三个元素来看

从i前面的某个元素(途中假设是从0开始)开头能包含i能包含i的共有(n-i)=3个元素,同理前面一共有i个元素,所以从i前面包含i的共有i*(n-i)次 - 然后判断i之后的元素

这里其实相当于从i后面的元素开始到i(注意不能超过i,因为超过i就如下图所示例子,算作从2为开始到第五个,就在第一种判断前i个的例子重合了)

所以后(n-i-1)个元素,每个元素只有一次能包括i,所以总共是(n-i-1)个
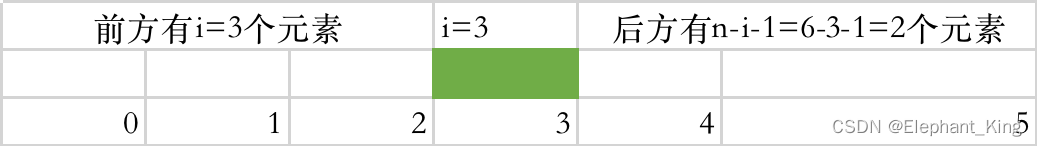
- 加上
i本身的一个
所以共有(i*(n-i))+(n-i-1)+1约分后为(i+1)(n-i),也就是我的题解中给出的表达式形式
本题还有一个注意事项,就是最后的总和是不能直接用double的,因为测试数据中有超过double范围的,我这里用的是long double,注意一下保留两位的long double输出printf中是%Ld
题解
#include<bits/stdc++.h>
using namespace std;
int main(){
//注意使用long double
long double sum=0.0;
long double data;
int n;
cin>>n;
for(int i=0;i<n;i++){
cin>>data;
//关于这个公式的推导,题解中给出了详细饿解释
sum+=data*(i+1)*(n-i);
}
//注意输出形式
printf("%.2Lf",sum);
}