NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis | NeRF: 用于视图合成的神经辐射场的场景表示 | 2020年
出自文献:Mildenhall B, Srinivasan P P, Tancik M, et al. Nerf: Representing scenes as neural radiance fields for view synthesis[C]//European Conference on Computer Vision. Springer, Cham, 2020: 405-421.
摘要
- 我们提出一种方法,使用较少的视图(view)作为输入,对一个连续、隐含的体积场景函数(volumetric scene function)进行优化,从而实现了关于复杂场景的新视图合成的最先进的结果。
- 我们的算法用全连接深度网络来表示场景,其输入是 5D 坐标:空间位置 ( x , y , z ) (x,y,z) (x,y,z) 和视角方向(viewing direction)$ (θ,ϕ)$;其输出是体积密度(volume density)和该空间位置上发射出来的辐射亮度(radiance,与视角相关)。
- 通过沿着相机光线(camera rays)获取 5D 坐标,使用经典的立体渲染(volume rendering)技术,我们将输出的颜色和密度投影到图像上,从而实现视图合成。
- 由于立体渲染是可导的,神经网络的优化,只需要提供一系列确定相机位姿的图像。
1 介绍
-
我们的工作,用新的方法解决了在
视图合成(view synthesis)
中长期以来的问题。
- 我们直接优化一个连续的 5D 场景表示(scene representation)的参数(网络权重),根据捕获到图像,最小化渲染误差。
- 我们把静态场景表示为连续的 5D 函数(指输入是 5D ),输出在各个空间点 ( x , y , z ) (x,y,z) (x,y,z) 和各个方向 ( θ , ϕ ) (θ,ϕ) (θ,ϕ) 发射出来的辐射亮度和密度(就像可导的透明度,控制穿过 ( x , y , z ) (x,y,z) (x,y,z) 的射线,可以累加多少辐射亮度)。
- 我们的方法是优化一个深度全连接的神经网络,没有用到卷积层,全连接神经网络又称多层感知器(MLP);我们用这个 MLP 来表示这样的函数:根据一个 5D 坐标 ( x , y , z , θ , ϕ ) (x,y,z,θ,ϕ) (x,y,z,θ,ϕ),回归输出一个体积密度和视角相关的 RGB 颜色。
-
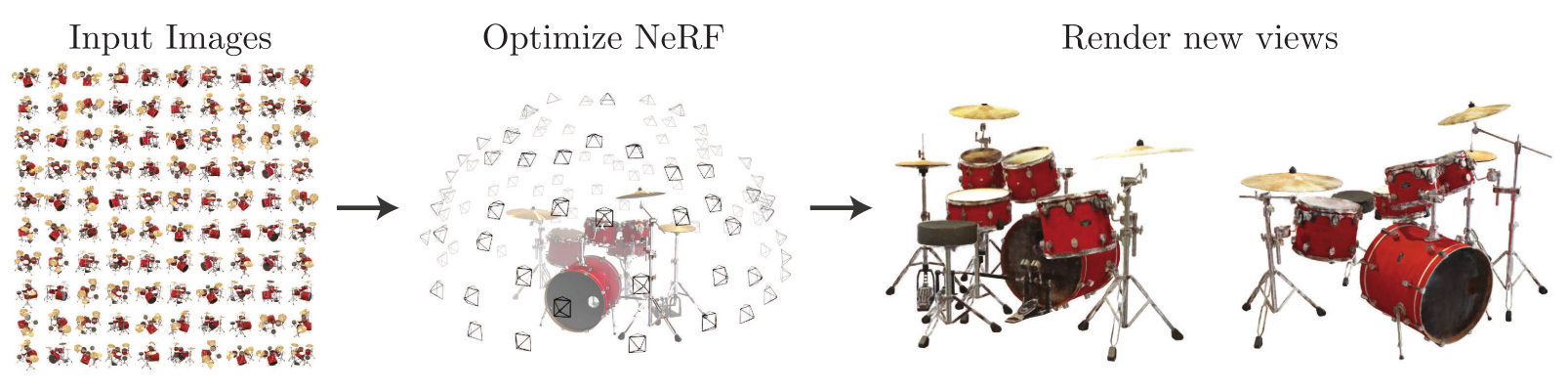
整个流水线如下图所示:
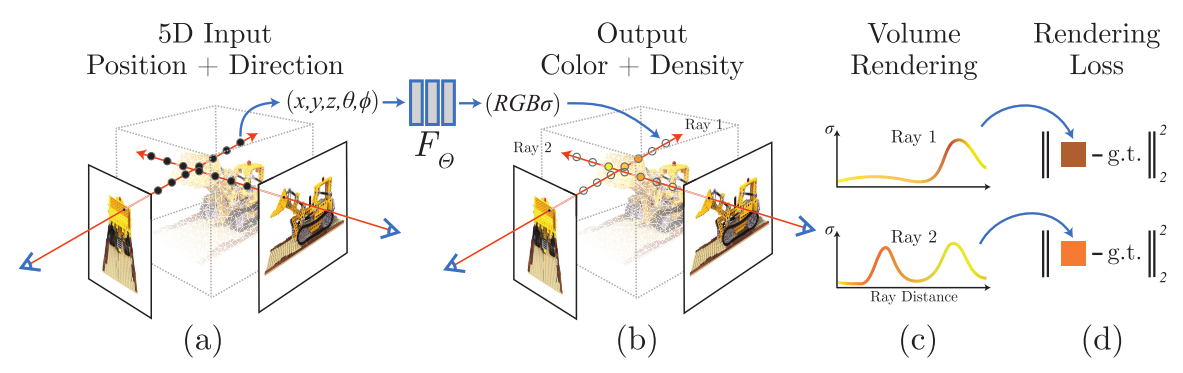
- 为了根据某一视角(viewpoint),渲染出这个神经辐射场(Neural Radiance Field, NeRF),我们:
-
- 使相机光线穿过场景,生成一组 3D 采样点;
- 让这些 3D 点和对应的 3D 视角方向作为神经网络的输入,生成一组颜色和密度;
- 使用经典的立体渲染技术,累加这些颜色和密度,得到 2D 图像。
- 由于以上过程是可导的,我们可以使用梯度下降来优化模型,最小化
观测图像与模型回归计算的图像之间的误差。- 这可以鼓励神经网络学习的场景模型具有一致性(coherent),即在包含场景内容的位置,可以得到较大的体积密度,和准确的颜色。
- 我们发现对于复杂的场景,用简单的方法优化 NeRF 效果不理想:
- 很难得到高分辨率的收敛结果;
- 也不能高效利用相机光线所需的采样点。
- 于是,我们这样解决以上问题:
- 用一个位置编码(positional encoding)对输入 5D 坐标进行变换,使得 MLP 可以表示高频函数;
- 提出层次化的采样流程(hierarchical sampling procedure),减少所需的采样点。
- 我们的方法保留了体积表示的优点:
- 可以表示复杂的几何和外观;
- 可以通过投影图像进行梯度下降的优化。
- 重要的是,我们的方法克服了体积表示的一个关键问题:在表示高分辨率的复杂场景时,离散的体素网格的存储空间成本非常高。
- 总结下来,本文的贡献如下:
- 包含复杂几何和材质的连续场景的表示方法:使用参数化为 MLP 的 5D 神经辐射场;
- 基于立体渲染技术的可导的渲染流程,用于网络的优化。其中还包括层次化的采样策略,专注于可见的场景内容(visible scene content),充分利用了 MLP 的容量。
- 使用位置编码,将输入 5D 坐标映射到更高维的空间,让 NeRF 可以学习表示高频的场景内容。
2 相关工作
3 神经辐射场的场景表示
我们把一个连续的场景表示为一个 5D 向量值函数(vector-valued function):
- 输入是 3D 位置 x = ( x , y , z ) x=(x,y,z) x=(x,y,z) 和 2D 视角方向 ( θ , ϕ ) (θ,ϕ) (θ,ϕ)
- 输出是发射颜色 c = ( r , g , b ) c=(r,g,b) c=(r,g,b) 和体积密度 σ σ σ。
在实际中,我们把视角方向表示为 3D 笛卡尔单位向量
d
d
d。我们用一个 MLP 网络来近似这个连续的 5D 场景表示:
F
Θ
:
(
x
,
d
)
→
(
c
,
σ
)
F_{\Theta}:(\mathbf{x}, \mathbf{d}) \rightarrow(\mathbf{c}, \sigma)
FΘ:(x,d)→(c,σ)
我们优化该网络的权重,使之对于每个输入 5D 坐标,都会得到对应的密度和有方向的发射颜色。
我们约束了预测体积密度 σ 的网络的输入仅仅是位置 X,而预测 RGB 颜色 C 的网络的输入是位置和视角方向,通过这种方式可以鼓励网络学习到多视角连续的表示。
- 在具体实现上,MLP F Θ F_{\Theta} FΘ 首先用 8 层的全连接层(使用 ReLU 激活函数,每层有 256 个通道),处理 3D 坐标 x x x,得到 σ σ σ 和一个 256 维的特征向量。
- 这个 256 维的特征向量,与视角方向一起拼接起来,喂给另一个全连接层(使用 ReLU 激活函数,每层有 128 个通道),输出方向相关的 RGB 颜色。
图 3 可以观察到,我们的方法可以表示出非朗伯体效应(non-Lambertian effects)。从图 4 可以观察到,如果训练模型时没有视角的依赖(只有 X 一个输入),那么模型会很难表示出高光(specularity)。


4 辐射场的立体渲染
我们的 5D 神经辐射场把场景表示为:任意空间点上的体积密度和有方向的辐射亮度。使用经典的立体渲染的原理,我们可以渲染出任意射线穿过场景的颜色。体积密度
σ
(
x
)
σ(x)
σ(x) 可以解释为:光线停留在位置 X� 处的无穷小粒子的可导概率。在最近和最远边界为
t
n
t_n
tn 和
t
f
t_f
tf 的条件下,相机光线
r
(
t
)
=
o
+
t
d
r(t)=o+td
r(t)=o+td 的颜色
C
(
r
)
C(r)
C(r)为:
C
(
r
)
=
∫
t
n
t
f
T
(
t
)
σ
(
r
(
t
)
)
c
(
r
(
t
)
,
d
)
d
t
,
where
T
(
t
)
=
exp
(
−
∫
t
n
t
σ
(
r
(
s
)
)
d
s
)
\begin{equation} C(\mathbf{r})=\int_{t_{n}}^{t_{f}} T(t) \sigma(\mathbf{r}(t)) \mathbf{c}(\mathbf{r}(t), \mathbf{d}) d t, \text { where } T(t)=\exp \left(-\int_{t_{n}}^{t} \sigma(\mathbf{r}(s)) d s\right) \end{equation}
C(r)=∫tntfT(t)σ(r(t))c(r(t),d)dt, where T(t)=exp(−∫tntσ(r(s))ds)
函数 $T(t) $表示沿着光线从 t n t_n tn 到 t t t 所累积的透明度(accumulated transmittance) ,即 光线从 t n t_n tn 出发到 t t t,穿过该路径的概率。视图的渲染需要求这个积分 C ( r ) C(r) C(r),它是就是虚拟相机穿过每个像素的相机光线,所得到的颜色。
我们使用求积法(quadrature)进行积分的数值求解。确定性的求积分不太适合 MLP,我们采用的是**分层抽样(stratified sampling)**的方法。我们把
[
t
n
,
t
f
]
[t_n,t_f]
[tn,tf]分成均匀分布的小区段,接着对每个小区段进行均匀采样:
t
i
∼
U
[
t
n
+
i
−
1
N
(
t
f
−
t
n
)
,
t
n
+
i
N
(
t
f
−
t
n
)
]
\begin{equation} t_{i} \sim \mathcal{U}\left[t_{n}+\frac{i-1}{N}\left(t_{f}-t_{n}\right), t_{n}+\frac{i}{N}\left(t_{f}-t_{n}\right)\right] \end{equation}
ti∼U[tn+Ni−1(tf−tn),tn+Ni(tf−tn)]
我们使用采样的样本,用积分法则来计算
C
(
r
)
C(r)
C(r):
C
^
(
r
)
=
∑
i
=
1
N
T
i
(
1
−
exp
(
−
σ
i
δ
i
)
)
c
i
,
where
T
i
=
exp
(
−
∑
j
=
1
i
−
1
σ
j
δ
j
)
\begin{equation} \hat{C}(\mathbf{r})=\sum_{i=1}^{N} T_{i}\left(1-\exp \left(-\sigma_{i} \delta_{i}\right)\right) \mathbf{c}_{i}, \text { where } T_{i}=\exp \left(-\sum_{j=1}^{i-1} \sigma_{j} \delta_{j}\right) \end{equation}
C^(r)=i=1∑NTi(1−exp(−σiδi))ci, where Ti=exp(−j=1∑i−1σjδj)
其中,
δ
i
=
t
i
+
1
−
t
i
\delta_{i}=t_{i+1}-t_{i}
δi=ti+1−ti 是相邻样本之间的距离。
5 神经辐射场的优化
前面所述的核心算法,还不够实现最先进的效果。因此我们还引入了两项优化措施,帮助模型能够表征高分辨率的复杂场景:
- 输入坐标的位置编码(positional encoding):帮助 MLP 能够表示高频函数;
- 层次化的采样方案(hierarchical sampling procedure),可以有效地采样模型的高频表示。
5.1 位置编码(positional encoding)
尽管神经网络理论上可以逼近任意函数,但我们发现,用网络 F Θ F_{\Theta} FΘ 直接处理输入坐标 x y z θ ϕ xyzθϕ xyzθϕ,很难表示出高频的细节。这符合 Rahaman 等人最近的工作,他们证明了深度网络倾向于学习到频率较低的函数。他们还证明,使用高频函数,把输入映射到更高维的空间中,再喂给神经网络,可以更好地拟合具有高频变化的数据。
我们把这部分理论应用到了神经场景表示,重新构建函数 F Θ F_{\Theta} FΘ,作为两个函数的组合函数: F Θ = F Θ ′ ∘ γ F_{\Theta}=F_{\Theta}^{\prime} \circ \gamma FΘ=FΘ′∘γ,该方法可以明显提高性能。
在这里,γ 表示一个从 R \mathbb{R} R 到更高维空间 R 2 L \mathbb{R}^{2L} R2L 的映射, F Θ ′ F_{\Theta}^{\prime} FΘ′是普通的 MLP。
我们使用的编码函数为:
γ
(
p
)
=
(
sin
(
2
0
π
p
)
,
cos
(
2
0
π
p
)
,
⋯
,
sin
(
2
L
−
1
π
p
)
,
cos
(
2
L
−
1
π
p
)
)
\begin{equation} \gamma(p)=\left(\sin \left(2^{0} \pi p\right), \cos \left(2^{0} \pi p\right), \cdots, \sin \left(2^{L-1} \pi p\right), \cos \left(2^{L-1} \pi p\right)\right) \end{equation}
γ(p)=(sin(20πp),cos(20πp),⋯,sin(2L−1πp),cos(2L−1πp))
该函数分别应用于
X
X
X 的三个坐标,以及视角方向单位向量
d
d
d 的三个坐标。
在本文示例中,对于 γ ( x ) γ(x) γ(x)设 L = 10 L=10 L=10;对于 γ ( d ) γ(d) γ(d) 设 L = 4 L=4 L=4。
与 Transformer 架构中使用的位置编码不同,我们这里的编码函数,是为了把连续的输入坐标映射到更高维的空间,好让 MLP 能够更好地近似高频的函数。
5.2 分层体积采样(Hierachical volume sampling)
我们的渲染策略,会沿着相机光线的 N 个查询点(query points),密集地计算神经辐射场。这种策略并不高效:空闲空间和遮挡的区域,并没有对渲染图像起作用,但是依然会进行重复地采样。我们借鉴了立体渲染的早起工作,提出了层次化表示来提升渲染效率:根据期望的渲染效果,来按比例地分配采样点。
于是我们并没有使用单个网络来表示场景,我们会同时优化两个网络:粗糙网络和精细网络。我们首先使用分层抽样,来采样第一个集合,包含 N c N_c Nc 个位置点,用方程(2)和(3)来计算粗糙网络。根据粗糙网络的输出,我们可以沿着光线生成更明智的采样点。
重写式子(3)中的粗糙网络
C
^
c
(
r
)
\hat{C}_{c}(\mathbf{r})
C^c(r):
C
^
c
(
r
)
=
∑
i
=
1
N
c
w
i
c
i
,
w
i
=
T
i
(
1
−
exp
(
−
σ
i
δ
i
)
)
\begin{equation} \hat{C}_{c}(\mathbf{r})=\sum_{i=1}^{N_{c}} w_{i} c_{i}, \quad w_{i}=T_{i}\left(1-\exp \left(-\sigma_{i} \delta_{i}\right)\right) \end{equation}
C^c(r)=i=1∑Ncwici,wi=Ti(1−exp(−σiδi))
把这些权重进行标准化:
w
^
i
=
w
i
/
∑
j
=
1
N
c
w
j
\hat{w}_{i}=w_{i} / \sum_{j=1}^{N_{c}} w_{j}
w^i=wi/∑j=1Ncwj。
我们使用逆变换采样(inverse transform sampling),从该分布采样出第二个集合,包含 N f N_f Nf 个位置。我们用第一个采样点集合和第二个采样点集合的并集上,计算我们的精细网络,最后使用所有 N c + N f N_c+N_f Nc+Nf 个样本,用方程(3)计算最终的光线颜色 C ^ f ( r ) \hat{C}_{f}(\mathbf{r}) C^f(r)。
使用这种方法,可以分配更多的样本点在包含场景内容的区域内。它解决了与**重要性抽样(importance sampling)**相同的目标。
5.3 实现细节
6 结果
6.1 数据集
6.2 对比
6.3 讨论
6.4 Ablation studies
7 结论
- 关于使用 MLP 作为连续函数,用来表示物体和场景的研究,我们克服了过去工作的不足。与过去基于 CNN 的常用方法相比,我们用 5D 神经辐射场(用 MLP 表示的函数,其输入是 3D 位置和 2D 视角方向,输出体积密度和视角相关的辐射亮度)来表示场景,生成了更好的渲染效果。
- 未来方向
- 尽管我们提出了分层体积采样的策略,实现用于渲染的高效采样,但未来仍然有很多研究工作的空间,来更高效地实现神经辐射场的优化和渲染。
- 后期工作的另一个方向是可解释性:诸如体素和网格的表示方法,可以很容易地推断渲染质量和失效模式(failure modes),但是当我们以深度神经网络的权重,对场景进行编码时,就不清楚如何分析这些问题。
- 我们希望本文的工作,可以推动基于真实世界图像的图形学流水线的发展,通过真实物体和场景的图像,复杂的场景都可以由神经辐射场来组成。


![[经验分享]gpt-3.5-Turbo|unity中实现http接口调用gpt新接口以及信息处理的实现案例分享](https://img-blog.csdnimg.cn/img_convert/35b82fcdfff6cc865aa0822e7ee2df54.png)



![[SSD科普] 固态硬盘物理接口SATA、M.2、PCIe常见疑问,如何选择?](https://img-blog.csdnimg.cn/img_convert/bd935ef409ed41ac81d233e736274501.png)