线段树模板初讲

引入

线段树是算法竞赛中常用的用来维护 区间信息 的数据结构。
线段树可以在$O(\log N)$ 的时间复杂度内实现单点修改、区间修改、区间查询（区间求和，求区间最大值，求区间最小值）等操作。
线段树所维护的信息，需要满足区间加法。
区间加法：如果一个区间 [l,r]
（线段树中一个点表示一个区间）满足区间加法的意思是一个区间 [l,r]的线段树维护的信息（即区间最大值，区间最小值，区间和，区间 gcd
等），可以由两个区间 [l,mid]和 [mid+1,r] 合并而来。

数据结构

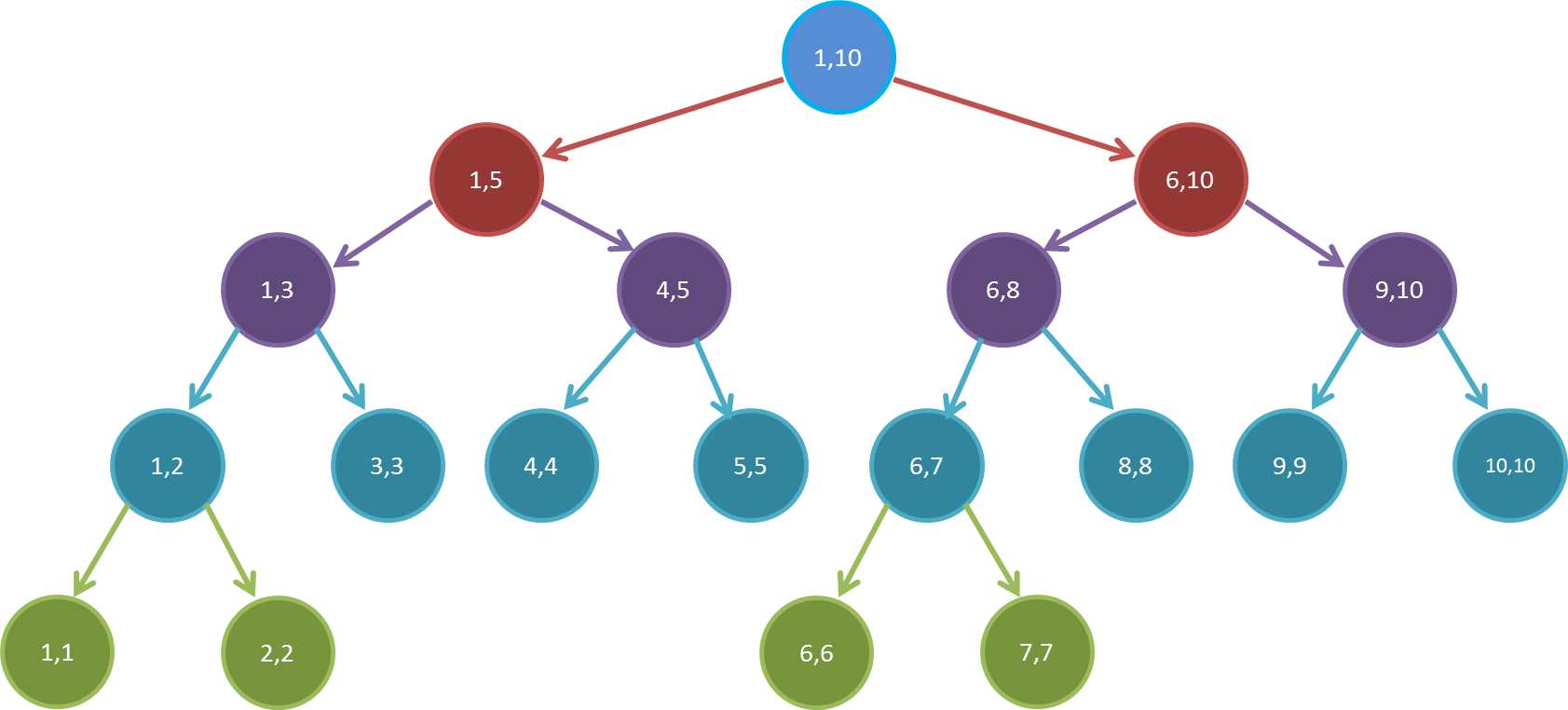
线段树特点

1. 每个节点表示一个区间$[l,r]$，并记录着区间中的一些性质。
2. 对于一个节点x，其区间为$[l,r]$，且$l\ne r$， $mid=\lfloor \frac{l+r}{2}\rfloor$。其子节点为$x<<1$和$x<<1|1$，它们的区间分别为$[l,mid]$、$[mid+1,r]$。
3. 其存储方式是堆的形式，也就是节点存于数组，父节点和子节点是2倍关系。
4. 线段树的存储数组大小一般是$4n$

线段树结构的Python实现

# 节点的定义
def Tree :
	def __init__(self) :
		# 用于描述节点表示区间
		self.l = 0
		self.r = 0
		# 节点表示区间的性质
		self.v = 0
		# 懒标记
		self.add = 0
tr = [Tree() for _ in range(N * 4)]

操作(以求和为例)

pushup

具体作用：根据子节点推导父节点的性质的值

def pushup(u) :
	tr[u].v = tr[u << 1].v + tr[u << 1 | 1].v

build

具体作用：根据已给信息构建线段树，也可以说是初始化。

def build(u, l, r) :
	tr[u].l, tr[u].r = l, r # 初始化节点区间
	if l == r : # 叶子节点，递归出口
		tr[u].v = a[l]
		return
	# 非叶子节点，继续递归构造子孙节点
	mid = l + r >> 1
	build(u << 1, l, mid)
	build(u << 1 | 1, mid + 1, r)
	pushup(u) # 用子节点更新当前节点的值

单点操作，区间查询

modify

对于单点修改，大致流程是，沿着包含目标节点的路径，找到目标节点并修改，最后回溯，用子节点将往上的节点更新。

def modify(u, x, d) :
	# 找到目标节点并修改
	if tr[u].l == x and tr[u].r == x :
		tr[u].v = d
		return
	# 未找到目标节点，继续延伸
	mid = tr[u].l + tr[u].r >> 1
	if x <= mid : # 节点在左半段情况
		modify(u << 1, x, d)
	else :
		modify(u << 1 | 1, x, d)
	pushup(u) # 更新当前区间节点值

query

向下递归的找区间的值。
如果目前递归的节点区间被包含在目标区间内，可以直接返回相应区间性质的值。
如果相交，与目标区间左相交或者右相交则可在相应子区间中查找被包含的区间值。

def query(u, l, r) :
	# 目前递归的节点区间被包含在目标区间内
	if l <= tr[u].l and tr[u].r <= r :
		return tr[u].v
	mid = tr[u].l + tr[u].r >> 1
	res = 0
	# 相交情况考虑
	if l <= mid : res = query(u << 1, l, r)
	if r > mid : res += query(u << 1 | 1, l, r)
	return res

区间操作，区间操作

如果要求修改区间 [l,r]，把所有包含在区间 [l,r] 中的节点都遍历一次、修改一次，时间复杂度无法承受。我们这里要引入一个叫做 「懒惰标记」 的东西。
懒惰标记，简单来说，就是通过延迟对节点信息的更改，从而减少可能不必要的操作次数。每次执行修改时，我们通过打标记的方法表明该节点对应的区间在某一次操作中被更改，但不更新该节点的子节点的信息。实质性的修改则在下一次访问带有标记的节点时才进行。

这里的懒惰标记一般只作用于当前节点的子节点区间性质计算上，并不会对本层节点有任何影响。

pushdown

作用：向下传懒标记，子节点性质根据懒标记修改，并将当前层懒标记去除。

def pushdown(u) :
	root, left, right = tr[u], tr[u << 1], tr[u << 1 | 1]
	# 向下传懒标记，子节点性质根据懒标记修改
	if root.add :
		left.add += root.add
		right.add += root.add
		left.v += (left.r - left.l + 1) * root.add
		right.v += (right.r - right.l + 1) * root.add
		root.add = 0 #将当前层懒标记去除

modify

额外操作：每次遇到目标区间包含的区间节点，进行修改性质和标记懒标记。
否则，需要进行递归处理子区间，在这之前要向下传递懒标记。

def modify(u, l, r, d) :
	# 遇到目标区间包含的区间节点
	if l <= tr[u].l and tr[u].r <= r :
		tr[u].add += d
		tr[u].v += (tr[u].r - tr[u].l + 1) * d
		return
	else :
		pushdown(u)
		mid = tr[u].l + tr[u].r >> 1
		if l <= mid : # 与左半段相交
			modify(u << 1, l, r, d)
		if r > mid : # 与右半段相交部分
			modify(u << 1 | 1, l, r, d)
		pushup(u)

query

额外操作：递归处理子区间，在这之前要向下传递懒标记。

def query(u, l, r) :
	# 目标区间包含当前节点区间
	if l <= tr[u].l and tr[u].r <= r :
		return tr[u].v
	else :
		# 下传懒标记
		pushdown(u)
		mid = tr[u].l + tr[u].r >> 1
		res = 0
		if l <= mid :
			res = query(m << 1, l, r)
		if l > mid :
			res += query(m << 1 | 1, l, r)
		return res

例题

AcWing 1275. 最大数

给定一个正整数数列 a1,a2,…,an，每一个数都在 0∼p−1之间。

可以对这列数进行两种操作：

添加操作：向序列后添加一个数，序列长度变成 n+1
；
询问操作：询问这个序列中最后 L
个数中最大的数是多少。
程序运行的最开始，整数序列为空。

一共要对整数序列进行 m
次操作。

写一个程序，读入操作的序列，并输出询问操作的答案。

输入格式
第一行有两个正整数 m,p
，意义如题目描述；

接下来 m
行，每一行表示一个操作。

如果该行的内容是 Q L，则表示这个操作是询问序列中最后 L
个数的最大数是多少；

如果是 A t，则表示向序列后面加一个数，加入的数是 (t+a) mod p
。其中，t
是输入的参数，a
是在这个添加操作之前最后一个询问操作的答案（如果之前没有询问操作，则 a=0
）。

第一个操作一定是添加操作。对于询问操作，L>0
且不超过当前序列的长度。

输出格式
对于每一个询问操作，输出一行。该行只有一个数，即序列中最后 L
个数的最大数。

数据范围
1≤m≤2×105
,
1≤p≤2×109
,
0≤t<p
输入样例：
10 100
A 97
Q 1
Q 1
A 17
Q 2
A 63
Q 1
Q 1
Q 3
A 99
输出样例：
97
97
97
60
60
97
样例解释
最后的序列是 97,14,60,96。

思路

一共两种操作

1. 向序列最后添加一个数
2. 询问序列最后L个数中最大的数
   单点操作、区间查询
   由于加入的最后一个数需要前一个最大的数来计算，所以每次都要记录前一个数。

代码

from sys import stdin
N = 200010

class Tree :
	def __init__(self) :
		self.l = 0
		self.r = 0
		self.v = 0 # 表示最大值
tr = [Tree() for _ in range(N * 4)]

def pushup(u) :
	tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v)

def build(u, l, r) :
	tr[u].l, tr[u].r = l, r
	if l == r :
		return
	mid = (l + r) >> 1
	build(u << 1, l, mid)
	build(u << 1 | 1, mid + 1, r)
	pushup(u)

def modify(u, x, c) :
	if tr[u].l == tr[u].r == x :
		tr[u].v = c
		return
	mid = tr[u].l + tr[u].r >> 1
	if x <= mid : modify(u << 1, x, c)
	else : modify(u << 1 | 1, x, c)
	pushup(u)

def query(u, l, r) :
	if l <= tr[u].l and tr[u].r <= r :
		return tr[u].v
	else :
		res = 0
		mid = tr[u].l + tr[u].r >> 1
		if mid >= l :
			res = query(u << 1, l, r)
		if r > mid :
			res = max(res, query(u << 1 | 1, l, r))
		return res

last, index = 0, 0
n, m = map(int, stdin.readline().split())

build(1, 1, n)
for i in range(n) :
	cmd = stdin.readline().split()
	op, c = cmd[0], int(cmd[1])
	if op == "Q" :
		last = query(1,index - c + 1 , index)
		print(last)
	else :
		modify(1, index + 1, (last + c) % last)
		index += 1

AcWing 243. 一个简单的整数问题2

给定一个长度为 N的数列 A，以及 M条指令，每条指令可能是以下两种之一：C l r d，表示把 A[l],A[l+1],…,A[r]都加上 d。Q l r，表示询问数列中第 l∼r个数的和。对于每个询问，输出一个整数表示答案。

输入格式
第一行两个整数 N,M。

第二行 N 个整数 A[i]。

接下来 M行表示 M条指令，每条指令的格式如题目描述所示。

输出格式
对于每个询问，输出一个整数表示答案。

每个答案占一行。

数据范围
1≤N,M≤105
,
|d|≤10000
,
|A[i]|≤109
输入样例：
10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4
输出样例：
4
55
9
15

思路

典型的区间操作，区间查询的题，懒标记出厂。

代码

from sys import stdin
N = 100010

class Tree :
	def __init__(self) :
		self.l = 0
		self.r = 0
		self.v = 0 # 表示区间和
		self.add = 0 # 懒标记

tr = [Tree() for _ in range(N * 4)]
a = [0] * N

def pushup(u) :
	tr[u].v = tr[u << 1].v + tr[u << 1 | 1].v

def pushdown(u) :
	root, left, right = tr[u], tr[u << 1], tr[u << 1 | 1]
	if root.add :
		left.add += root.add
		right.add += root.add
		left.v += (left.r - left.l + 1) * root.add
		right.v += (right.r - right.l + 1) * root.add
		root.add = 0

def build(u, l, r) :
	tr[u].l, tr[u].r = l, r
	if l == r :
		tr[u].v = a[l]
		return
	mid  = l + r >> 1
	build(u << 1, l, mid)
	build(u << 1 | 1, mid + 1, r)
	pushup(u)

def modify(u, l, r, d) :
	if l <= tr[u].l and tr[u].r <= r :
		tr[u].v += (tr[u].r - tr[u].l + 1) * d
		tr[u].add += d
		return
	pushdown(u)
	mid = tr[u].l + tr[u].r >> 1
	if l <= mid :
		modify(u << 1, l, r, d)
	if r > mid :
		modify(u << 1 | 1, l, r, d)
	pushup(u)

def query(u, l, r) :
	if l <= tr[u].l and tr[u].r <= r :
		return tr[u].v
	pushdown(u)
	mid  = tr[u].l + tr[u].r >> 1
	res = 0
	if l <= mid :
		res = query(u << 1, l, r)
	if r > mid :
		res += query(u << 1 | 1, l, r)
	return res

n, m = map(int, input().split())
a[1 : n + 1] = list(map(int, input().split()))

build(1, 1, n)

for _ in range(m) :
	cmd = stdin.readline().split()
	op, l, r = cmd[0], int(cmd[1]), int(cmd[2])
	if op == 'Q' :
		print(query(1, l, r))
	else :
		d = int(cmd[3])
		modify(1, l, r, d)

总结

线段树就是牛，上面是关于线段树的简单讲解，分别关于区间查询，区间操作，和单点操作。对于线段树更多性质的记录和结合，可以解决很多很神奇的同时，但也就会使关系复杂。这个我们下次再言。