目录

1. 移除链表元素  ★

2. K 个一组翻转链表  ★★★

3. 三角形最小路径和  ★★

---

1. 移除链表元素

给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回 新的头节点 。

示例 1：

输入：head = [1,2,6,3,4,5,6], val = 6
输出：[1,2,3,4,5]

示例 2：

输入：head = [], val = 1
输出：[]

示例 3：

输入：head = [7,7,7,7], val = 7
输出：[]

提示：

• 列表中的节点数目在范围 [0, 104] 内
• 1 <= Node.val <= 50
• 0 <= val <= 50

代码：

class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None

class Solution(object):
    def removeElements(self, head, val):
        """
        :type head: ListNode
        :type val: int
        :rtype: ListNode
        """
        p = ListNode(0)
        p.next = head
        while p.next:
            if p.next.val == val:
                if p.next == head:
                    head = head.next
                    p.next = head
                else:
                    p.next = p.next.next
            else:
                p = p.next
        return head

# %%
class LinkList:
    def __init__(self):
        self.head = None
    def initList(self, data):
        if not data: return None
        self.head = ListNode(data[0])
        p = head = self.head
        for i in data[1:]:
            node = ListNode(i)
            p.next = node
            p = p.next
        return head
    def showList(self, head):
        if head:
            print(head.val, end = '->')
            self.showList(head.next)
        else:
            print('null')

if __name__ == '__main__':
    s = Solution()
    l = LinkList()
    head = l.initList([1,2,6,3,4,5,6])
    l.showList(head)
    head = s.removeElements(head, 6)
    l.showList(head)

输出：

1->2->6->3->4->5->6->null
1->2->3->4->5->null

---

2. K 个一组翻转链表

给你一个链表，每 k 个节点一组进行翻转，请你返回翻转后的链表。

k 是一个正整数，它的值小于或等于链表的长度。

如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

进阶：

• 你可以设计一个只使用常数额外空间的算法来解决此问题吗？
• 你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：

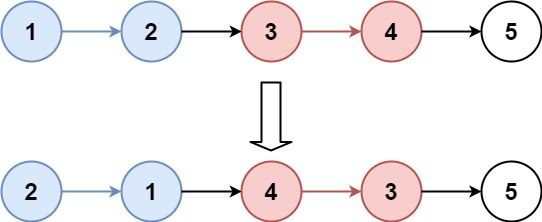
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

示例 2：

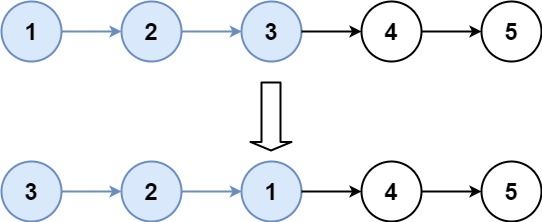
输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]

示例 3：

输入：head = [1,2,3,4,5], k = 1
输出：[1,2,3,4,5]

示例 4：

输入：head = [1], k = 1
输出：[1]

提示：

• 列表中节点的数量在范围 sz 内
• 1 <= sz <= 5000
• 0 <= Node.val <= 1000
• 1 <= k <= sz

代码：

class ListNode(object):
    def __init__(self, x):
        self.val = x
        self.next = None
class LinkList:
    def __init__(self):
        self.head = None
    def initList(self, data):
        self.head = ListNode(data[0])
        r=self.head
        p = self.head
        for i in data[1:]:
            node = ListNode(i)
            p.next = node
            p = p.next
        return r
    def convert_list(self,head):
        ret = []
        if head == None:
            return
        node = head
        while node != None:
            ret.append(node.val)
            node = node.next
        return ret

class Solution(object):
    def reverseKGroup(self, head, k):
        if head is None:
            return None
        index = 0
        lead, last = 0, 0
        pos = head
        temp = ListNode(-1)
        temp.next = head
        head = temp
        start = head
        while pos is not None:
            if index % k == k - 1:
                last = pos.next
                start = self.reverseList(start, last)
                pos = start
            pos = pos.next
            index += 1
        return head.next
    def reverseList(self, head, end):
        pos = head.next
        last = end
        next_start = pos
        while pos != end:
            head.next = pos
            last_pos = pos
            pos = pos.next
            last_pos.next = last
            last = last_pos
        return next_start

# %%
l = LinkList()
head = [1,2,3,4,5]
l1 = l.initList(head)
s = Solution()
print(l.convert_list(s.reverseKGroup(l1, k = 2)))

l2 = l.initList(head)
print(l.convert_list(s.reverseKGroup(l2, k = 3)))

输出：

[2, 1, 4, 3, 5]
[3, 2, 1, 4, 5]

---

3. 三角形最小路径和

给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

示例 1：

输入：triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出：11
解释：如下面简图所示：
2
3 4
6 5 7
4 1 8 3
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

示例 2：

输入：triangle = [[-10]]
输出：-10

提示：

• 1 <= triangle.length <= 200
• triangle[0].length == 1
• triangle[i].length == triangle[i - 1].length + 1
• -10^4 <= triangle[i][j] <= 10^4

进阶：

• 你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题吗？

代码：

class Solution(object):
    def minimumTotal(self, triangle):
        """
        :type triangle: List[List[int]]
        :rtype: int
        """
        n = len(triangle)
        dp = triangle[-1]
        for i in range(n - 2, -1, -1):
            for j in range(i + 1):
                dp[j] = triangle[i][j] + min(dp[j], dp[j + 1])
        #print(dp)
        return dp[0]

if __name__ == '__main__':
    s = Solution()

    triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
    print(s.minimumTotal(triangle))

    print(s.minimumTotal([[-10]]))

输出：

11
-10

---

附录

单链表

以“结点的序列”表示线性表称作线性链表（单链表），单链表是链式存取的结构。

链表中的数据是以结点来表示的，每个结点的构成：元素(数据元素的映象) + 指针(指示后继元素存储位置)，元素就是存储数据的存储单元，指针就是连接每个结点的地址数据。

存储方法

链接方式存储的线性表简称为链表（Linked List）。
链表的具体存储表示为：
① 用一组任意的存储单元来存放线性表的结点（这组存储单元既可以是连续的，也可以是不连续的）
② 链表中结点的逻辑次序和物理次序不一定相同。为了能正确表示结点间的逻辑关系，在存储每个结点值的同时，还必须存储指示其后继结点的地址（或位置）信息（称为指针（pointer）或链(link)）
链式存储是最常用的存储方式之一，它不仅可用来表示线性表，而且可用来表示各种非线性的数据结构。

结点结构

data域--存放结点值的数据域
next域--存放结点的直接后继的地址（位置）的指针域（链域）
链表通过每个结点的链域将线性表的n个结点按其逻辑顺序链接在一起的，每个结点只有一个链域的链表称为单链表（Single Linked List）。

头指针head和尾结点

单链表中每个结点的存储地址是存放在其前趋结点next域中，而开始结点无前趋，故应设头指针head指向开始结点。链表由头指针唯一确定，单链表可以用头指针的名字来命名。终端结点无后继，故尾结点的指针域为空，即NULL。