【深度学习】扩散模型(Diffusion Model)详解
文章目录
- 【深度学习】扩散模型(Diffusion Model)详解
- 1. 介绍
- 2. 具体方法
- 2.1 扩散过程
- 2.2 逆扩散过程
- 2.3 损失函数
- 3. 总结
- 4. 参考
1. 介绍

扩散模型有两个过程:
-
扩散过程:如上图所示,扩散过程为从右到左 X 0 → X T X_0 \rightarrow X_T X0→XT 的过程,表示对图片逐渐加噪,且 X t + 1 X_{t+1} Xt+1是在 X t X_{t} Xt上加躁得到的,其只受 X t X_{t} Xt的影响。因此扩散过程是一个马尔科夫过程。
- X 0 X_0 X0表示从真实数据集中采样得到的一张图片,对 X 0 X_0 X0添加 T T T 次噪声,图片逐渐变得模糊。当 T T T 足够大时, X T X_T XT为标准正态分布。在训练过程中,每次添加的噪声是已知的,即 q ( X t ∣ X t − 1 ) q(X_t|X_{t-1}) q(Xt∣Xt−1) 是已知的。根据马尔科夫过程的性质,我们可以递归得到 q ( X t ∣ X 0 ) q(X_t|X_0) q(Xt∣X0),即 q ( X t ∣ X 0 ) q(X_t|X_0) q(Xt∣X0) 是已知的。
其中,扩散过程最主要的是 q ( X t ∣ X 0 ) q(X_t|X_0) q(Xt∣X0) 和 q ( X t ∣ X t − 1 ) q(X_t|X_{t-1}) q(Xt∣Xt−1)的推导。
-
逆扩散过程:如上图所示,逆扩散过程为从左到右 X T → X 0 X_T \rightarrow X_0 XT→X0 的过程,表示从噪声中逐渐复原出图片。如果我们能够在给定 X t X_t Xt 条件下知道 X t − 1 X_{t-1} Xt−1 的分布,即如果我们可以知道 q ( X t − 1 ∣ X t ) q(X_{t-1}|X_t) q(Xt−1∣Xt),那我们就能够从任意一张噪声图片中经过一次次的采样得到一张图片而达成图片生成的目的。
- 显然我们很难知道 q ( X t − 1 ∣ X t ) q(X_{t-1}|X_t) q(Xt−1∣Xt),因此我们才会用 p Θ ( X t − 1 ∣ X t ) p_{Θ}(X_{t-1}|X_t) pΘ(Xt−1∣Xt) 来近似 q ( X t − 1 ∣ X t ) q(X_{t-1}|X_t) q(Xt−1∣Xt),而 p Θ ( X t − 1 ∣ X t ) p_{Θ}(X_{t-1}|X_t) pΘ(Xt−1∣Xt) 就是我们要训练的网络,在原文中就是个U-Net。而很妙的是,虽然我们不知道 q ( X t − 1 ∣ X t ) q(X_{t-1}|X_t) q(Xt−1∣Xt),但是 q ( X t − 1 ∣ X t X 0 ) q(X_{t-1}|X_tX_0) q(Xt−1∣XtX0) 却是可以用 q ( X t ∣ X 0 ) q(X_t|X_0) q(Xt∣X0) 和 q ( X t ∣ X t − 1 ) q(X_t|X_{t-1}) q(Xt∣Xt−1) 表示的,即 q ( X t − 1 ∣ X t X 0 ) q(X_{t-1}|X_tX_0) q(Xt−1∣XtX0) 是可知的,因此我们可以用 q ( X t − 1 ∣ X t X 0 ) q(X_{t-1}|X_tX_0) q(Xt−1∣XtX0) 来指导 p Θ ( X t − 1 ∣ X t ) p_{Θ}(X_{t-1}|X_t) pΘ(Xt−1∣Xt) 进行训练。
其中,逆扩散过程最主要的是 q ( X t − 1 ∣ X t X 0 ) q(X_{t-1}|X_tX_0) q(Xt−1∣XtX0)的推导。
2. 具体方法
在上面的介绍中,我们已经明确了要训练 p Θ ( X t − 1 ∣ X t ) p_{Θ}(X_{t-1}|X_t) pΘ(Xt−1∣Xt),但是目标函数如何确定?
有两个很直接的想法:
- 负对数的最大似然概率,即 − l o g p Θ ( X 0 ) -logp_{Θ}(X_0) −logpΘ(X0);
- 真实分布与预测分布的交叉熵,即 − E q ( X 0 ) l o g p Θ ( X 0 ) -E_{q(X_0)}logp_{Θ}(X_0) −Eq(X0)logpΘ(X0)。
但是这两种方法都很难去求解(求积分)和优化。因此扩散模型参考了VAE,不去优化这两个东西,而是优化他们的变分上界(variational lower bound),定义
L
V
L
B
L_{VLB}
LVLB,如下:

即
L
V
L
B
L_{VLB}
LVLB 减小就代表着
−
l
o
g
p
Θ
(
X
0
)
-logp_{Θ}(X_0)
−logpΘ(X0) 和
−
E
q
(
X
0
)
l
o
g
p
Θ
(
X
0
)
-E_{q(X_0)}logp_{Θ}(X_0)
−Eq(X0)logpΘ(X0) 的上界减小。且经过推导,$L_{VLB}又可写成如下形式:
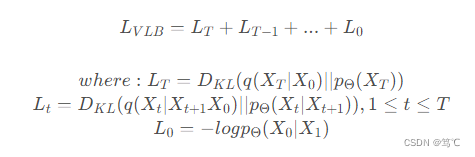
由上式不难发现, L t L_{t} Lt就是逆扩散过程中 q ( X t ∣ X t + 1 X 0 ) q(X_{t}|X_{t+1}X_0) q(Xt∣Xt+1X0) 和 p Θ ( X t ∣ X t + 1 ) p_{Θ}(X_{t}|X_{t+1}) pΘ(Xt∣Xt+1) 的 K L KL KL 散度,即用 q ( X t ∣ X t + 1 X 0 ) q(X_{t}|X_{t+1}X_0) q(Xt∣Xt+1X0) 来指导 p Θ ( X t ∣ X t + 1 ) p_{Θ}(X_{t}|X_{t+1}) pΘ(Xt∣Xt+1) 进行训练。这部分主要就是(1)式和(2)式的推导,细节部分见下文的损失函数。
2.1 扩散过程
如上图所示,扩散过程为从右到左 X 0 → X T X_0 \rightarrow X_T X0→XT 的过程,表示对图片逐渐加噪。
- X t + 1 X_{t+1} Xt+1是在 X t X_{t} Xt上加躁得到的,其只受 X t X_{t} Xt的影响。因此扩散过程是一个马尔科夫过程。
下面,我们对扩散过程进行推导:
由于每一步扩散的步长受变量
{
β
t
∈
(
0
,
1
)
}
t
=
1
T
\{β_{t} \in (0,1)\}_{t=1}^{T}
{βt∈(0,1)}t=1T 的影响。
q
(
X
t
∣
X
t
−
1
)
q(X_{t}|X_{t-1})
q(Xt∣Xt−1) 可写为如下形式,即给定
X
t
−
1
X_{t-1}
Xt−1 的条件下,
X
t
X_{t}
Xt服从均值为
1
−
β
t
X
t
−
1
\sqrt{1-β_{t}}X_{t-1}
1−βtXt−1,方差为
β
t
I
β_{t}I
βtI的正态分布:
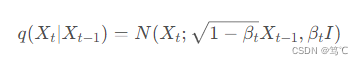
用重参数化技巧表示
X
t
X_{t}
Xt,令
α
t
=
1
−
β
t
α_{t}=1-β_{t}
αt=1−βt ,令
Z
t
∼
N
(
0
,
I
)
,
t
≥
0
Z_{t} \sim N(0,I), t \ge 0
Zt∼N(0,I),t≥0,即:
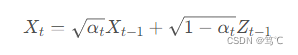
其中,
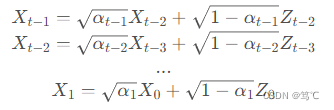
可以得到,令
α
ˉ
t
=
∏
i
=
1
t
α
i
\bar{α}_{t}= {\textstyle \prod_{i=1}^{t}α_{i}}
αˉt=∏i=1tαi :
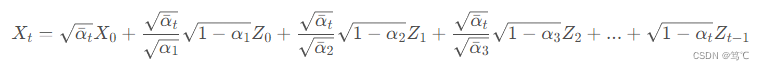
设随机变量
Z
ˉ
t
−
1
\bar{Z}_{t-1}
Zˉt−1 为:
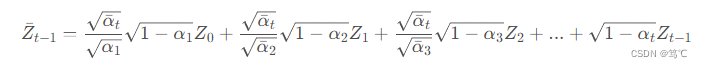
则
Z
ˉ
t
−
1
\bar{Z}_{t-1}
Zˉt−1 的期望和方差如下:
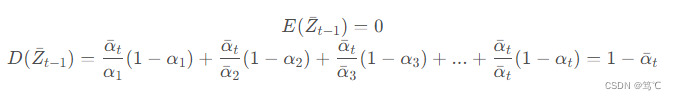
因此,
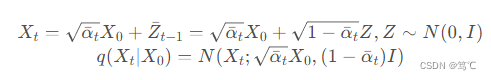
至此,我们推出了 q ( X t ∣ X t − 1 ) q(X_{t}|X_{t-1}) q(Xt∣Xt−1) 和 q ( X t ∣ X 0 ) q(X_{t}|X_{0}) q(Xt∣X0),完成了扩散过程。
2.2 逆扩散过程
如上图所示,逆扩散过程为从左到右 X T → X 0 X_T \rightarrow X_0 XT→X0 的过程,表示从噪声中逐渐复原出图片。
- 如果我们能够在给定 X t X_t Xt 条件下知道 X t − 1 X_{t-1} Xt−1 的分布,即如果我们可以知道 q ( X t − 1 ∣ X t ) q(X_{t-1}|X_t) q(Xt−1∣Xt),那我们就能够从任意一张噪声图片中经过一次次的采样得到一张图片而达成图片生成的目的。
- 显然我们很难知道 q ( X t − 1 ∣ X t ) q(X_{t-1}|X_t) q(Xt−1∣Xt),因此我们才会用 p Θ ( X t − 1 ∣ X t ) p_{Θ}(X_{t-1}|X_t) pΘ(Xt−1∣Xt) 来近似 q ( X t − 1 ∣ X t ) q(X_{t-1}|X_t) q(Xt−1∣Xt),而 p Θ ( X t − 1 ∣ X t ) p_{Θ}(X_{t-1}|X_t) pΘ(Xt−1∣Xt) 就是我们要训练的网络。
虽然我们不知道 q ( X t − 1 ∣ X t ) q(X_{t-1}|X_t) q(Xt−1∣Xt),但是 q ( X t − 1 ∣ X t X 0 ) q(X_{t-1}|X_tX_0) q(Xt−1∣XtX0) 却是可以用 q ( X t ∣ X 0 ) q(X_t|X_0) q(Xt∣X0) 和 q ( X t ∣ X t − 1 ) q(X_t|X_{t-1}) q(Xt∣Xt−1) 表示的,即 q ( X t − 1 ∣ X t X 0 ) q(X_{t-1}|X_tX_0) q(Xt−1∣XtX0) 是可知的。
- 因此我们可以用 q ( X t − 1 ∣ X t X 0 ) q(X_{t-1}|X_tX_0) q(Xt−1∣XtX0) 来指导 p Θ ( X t − 1 ∣ X t ) p_{Θ}(X_{t-1}|X_t) pΘ(Xt−1∣Xt) 进行训练。
下面我们对逆扩散过程进行推导:
先对
q
(
X
t
−
1
∣
X
t
X
0
)
q(X_{t-1}|X_tX_0)
q(Xt−1∣XtX0)进行推导:
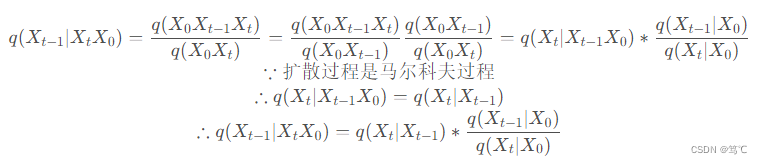
现在,我们已经把
q
(
X
t
−
1
∣
X
t
X
0
)
q(X_{t-1}|X_tX_0)
q(Xt−1∣XtX0)用
q
(
X
t
∣
X
0
)
q(X_t|X_0)
q(Xt∣X0)和
q
(
X
t
∣
X
t
−
1
)
q(X_t|X_{t-1})
q(Xt∣Xt−1) 进行表示,下面对
q
(
X
t
−
1
∣
X
t
X
0
)
q(X_{t-1}|X_tX_0)
q(Xt−1∣XtX0) 的表达式进行推导:
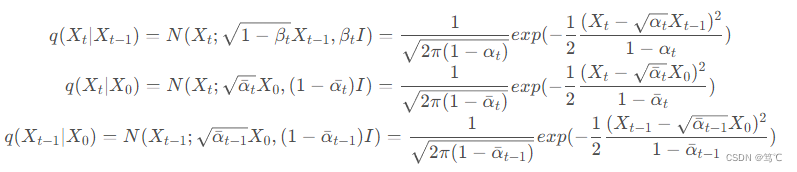
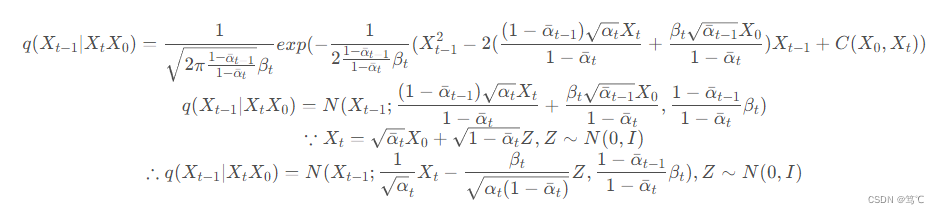
至此,我们得到了
q
(
X
t
−
1
∣
X
t
X
0
)
q(X_{t-1}|X_tX_0)
q(Xt−1∣XtX0)的分布表达式,完成了逆扩散过程。
2.3 损失函数
我们已经明确了要训练 p Θ ( X t − 1 ∣ X t ) p_{Θ}(X_{t-1}|X_t) pΘ(Xt−1∣Xt),那要怎样进行训练?有两个很直接的想法:
- 一个是负对数的最大似然概率,即 − l o g p Θ ( X 0 ) -logp_{Θ}(X_0) −logpΘ(X0);
- 另一个是真实分布与预测分布的交叉熵,即 − E q ( X 0 ) l o g p Θ ( X 0 ) -E_{q(X_0)}logp_{Θ}(X_0) −Eq(X0)logpΘ(X0)。
然而,类似于VAE,由于我们很难对噪声空间进行积分,因此直接优化 − l o g p Θ -logp_{Θ} −logpΘ 或 E q ( X 0 ) l o g p Θ ( X 0 ) E_{q(X_0)}logp_{Θ}(X_0) Eq(X0)logpΘ(X0)都是很困难的。
因此我们不直接优化它们,而是优化它们的变分上界
L
V
L
B
L_{VLB}
LVLB,其定义如下:
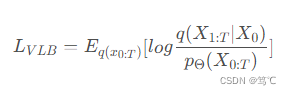
下面证明
L
V
L
B
L_{VLB}
LVLB 是
−
l
o
g
p
Θ
(
X
0
)
-logp_{Θ}(X_0)
−logpΘ(X0) 和
−
E
q
(
X
0
)
l
o
g
p
Θ
(
X
0
)
-E_{q(X_0)}logp_{Θ}(X_0)
−Eq(X0)logpΘ(X0) 的上界,即证明
L
V
L
B
≥
−
l
o
g
p
Θ
(
X
0
)
L_{VLB} \ge -logp_{Θ}(X_0)
LVLB≥−logpΘ(X0) 和
L
V
L
B
≥
−
E
q
(
X
0
)
l
o
g
p
Θ
(
X
0
)
L_{VLB} \ge -E_{q(X_0)}logp_{Θ}(X_0)
LVLB≥−Eq(X0)logpΘ(X0):
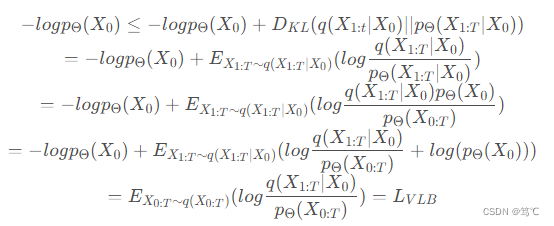
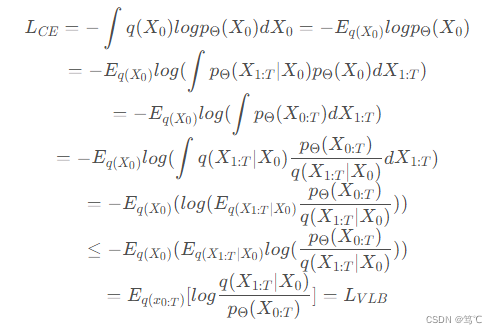
至此,证明了
L
V
L
B
L_{VLB}
LVLB 是
−
l
o
g
p
Θ
(
X
0
)
-logp_{Θ}(X_0)
−logpΘ(X0)和
−
E
q
(
X
0
)
l
o
g
p
Θ
(
X
0
)
-E_{q(X_0)}logp_{Θ}(X_0)
−Eq(X0)logpΘ(X0)的上界。进而,对
L
V
L
B
L_{VLB}
LVLB进行化简,得到:

从
L
t
L_{t}
Lt 即可看出,对
p
Θ
(
X
t
∣
X
t
+
1
)
p_{Θ}(X_{t}|X_{t+1})
pΘ(Xt∣Xt+1) 的监督就是最小化
p
Θ
(
X
t
∣
X
t
+
1
)
p_{Θ}(X_{t}|X_{t+1})
pΘ(Xt∣Xt+1) 和
q
(
X
t
∣
X
t
+
1
X
0
)
q(X_t|X_{t+1}X_0)
q(Xt∣Xt+1X0) 的KL散度。
3. 总结
总结来说,扩散模型的目的是希望学习出一个
p
Θ
(
X
t
−
1
∣
X
t
)
p_{Θ}(X_{t-1}|X_t)
pΘ(Xt−1∣Xt),即能够从噪声图恢复出原图。
为了达到这一个目的,我们使用
q
(
X
t
−
1
∣
X
t
X
0
)
q(X_{t-1}|X_tX_0)
q(Xt−1∣XtX0) 来监督
p
Θ
(
X
t
−
1
∣
X
t
)
p_{Θ}(X_{t-1}|X_t)
pΘ(Xt−1∣Xt) 进行训练,而
q
(
X
t
−
1
∣
X
t
X
0
)
q(X_{t-1}|X_tX_0)
q(Xt−1∣XtX0) 是可以用
q
(
X
t
∣
X
0
)
q(X_t|X_0)
q(Xt∣X0)和
q
(
X
t
∣
X
t
−
1
)
q(X_t|X_{t-1})
q(Xt∣Xt−1) 进行表示的,即
q
(
X
t
−
1
∣
X
t
X
0
)
q(X_{t-1}|X_tX_0)
q(Xt−1∣XtX0)是已知的。
4. 参考
【1】https://blog.csdn.net/Little_White_9/article/details/124435560
【2】https://lilianweng.github.io/posts/2021-07-11-diffusion-models/
【3】https://arxiv.org/abs/2105.05233
【4】https://arxiv.org/abs/1503.03585
【5】https://arxiv.org/abs/2006.11239








![[1.1_1]计算机系统概述——操作系统的概念、功能和目标](https://img-blog.csdnimg.cn/img_convert/c06e19f2aa66fdabcc8e9e32293a3bdc.png)
![[架构之路-126]-《软考-系统架构设计师》-操作系统-5-虚拟化技术、Docker与虚拟机比较](https://img-blog.csdnimg.cn/img_convert/6682a532785ae32d6f4d992ea27d2458.png)