目录

0.前言

1. 用数组表示存储一棵完全二叉树

2. 数组表示的完全二叉树的性质

3. 堆的基本概念

3.1 堆的核心性质

3.2 堆顶的性质

3.3 堆的单支性质

3.4 堆的左右支关系

4.  用代码实现堆

4.1 堆类的实现

4.2  堆的初始化

4.3 堆的销毁

4.4 获取堆顶的数据

4.5 堆判空

4.6 堆的大小

4.7 堆内元素的交换

4.8* 堆的插入

4.8.1 问题引入

4.8.2* 向上调整

4.8.3 堆插入的代码

4.9* 堆的删除

4.9.1 情景引入

4.9.2* 向下调整

4.9.3 堆的删除代码实现

---

0.前言

5堆的实现 · onlookerzy123456qwq/data_structure_practice_primer - 码云 - 开源中国 (gitee.com)https://gitee.com/onlookerzy123456qwq/data_structure_practice_primer/tree/master/5%E5%A0%86%E7%9A%84%E5%AE%9E%E7%8E%B0本文所有代码都已放到gitee，可以自取。

我们之前在博客当中，知道了如何构建一棵二叉树的方式3. 如何用代码表示一棵树，完全二叉树作为一种特殊的二叉树，我们也是可以用数组表示出来的！那如何表示呢？数据结构 堆 是一棵完全二叉树，那堆又有什么性质，如何在数组中实现堆呢？本文讲带你一一解答！

1. 用数组表示存储一棵完全二叉树

2.3 完全二叉树对于完全二叉树来说，完全二叉树的所有节点，在顺序上，是连续的，没有跳跃间隔的！！！

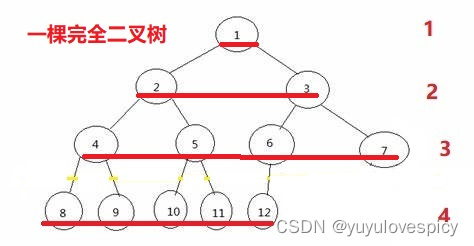
所以我们可以从第一层的第一个节点，自上层到下层，同一层自最左节点到最右节点，到最后一层的最后一个节点，都是连续的，没有跳跃间隔的，如上述节点是1 2 3 4 5 6 7......12。

所以对于一棵完全二叉树，所有的节点都是连续的，数组就是一个连续的没有跳跃间隔的存储结构，所以对于一棵完全二叉树，我们可以抽象为一个数组，给每一个节点数据都设计一个下标index，依次从上层到下层，同一层从最左到最右，连续存储到数组当中，如下图例子：

 我们就是这样用数组表示一棵完全二叉树的。为什么这么说？因为只要你知道了一个节点的在完全二叉树的位置，比如你是第3层的第2个节点，那从第一层的第一个根节点开始数（连续的没有间隔跳跃的），你就是第 2^2 - 1 + 2 == 5，即你是第5个节点。所以就可以快速定位你这个节点在数组当中存储的位置就是第5个元素，下标就是[4]。

也就是说，完全二叉树的所有的节点从上往下，从左到右，是连续的依次的按照下标连续存储的。

2. 数组表示的完全二叉树的性质

我们现在每一个节点存储在数组里，他们的就可以用一个下标index来定位，从下标代表的角度出发，那节点与节点之间的下标有关系吗？尤其是父节点和子节点直接有关系吗？兄弟节点之间有关系吗？我们直接上结论：

1. 根节点的下标始终为0。

2. 如果一个节点的下标是parent_i，那么它的左孩子的存储下标left_child是parent_i * 2 + 1，右孩子的存储下标right_child就是parent_i * 2 + 2。

（当然需要保证这个节点有左孩子 / 右孩子，不能超过下标的范围哦！）

3. 如果一个节点的下标是child，那么不管这个节点是左孩子，还是右孩子，它的父亲的下标一定就是（child - 1）/ 2。

（当然根节点除外，它没有父亲）

4. 如果一个节点的下标是index，那么在同一层中，它的左边的 亲兄弟 / 堂兄弟，的下标就是index-1，它的右边的 亲兄弟 / 堂兄弟，的下标就是index+1。

（当然存在三个特殊情况，一个是index是最后一个节点，右边不存在 亲兄弟/堂兄弟；另一个是我index节点是当前层的第一个节点，index-1就是上一层的最后一个节点；还有一个是我index节点是当前层的最后一个节点，那index+1就是下一层的第一个节点）

随便举个例子，B的存储下标是1，那我们快速定位B的左孩子和右孩子的下标：left_child = 1*2 + 1 == 3，right_child = 1*2 + 2 == 4，图中左孩子D节点的下标就是3，右孩子E节点的下标就是4。

节点D的下标是3，那在同一层中，3+1 = 4，我的右边相邻的 亲兄弟 / 堂兄弟，就是E（下标为4），3 - 1 = 2，那就是上一层的最后一个节点C（下标为2）。

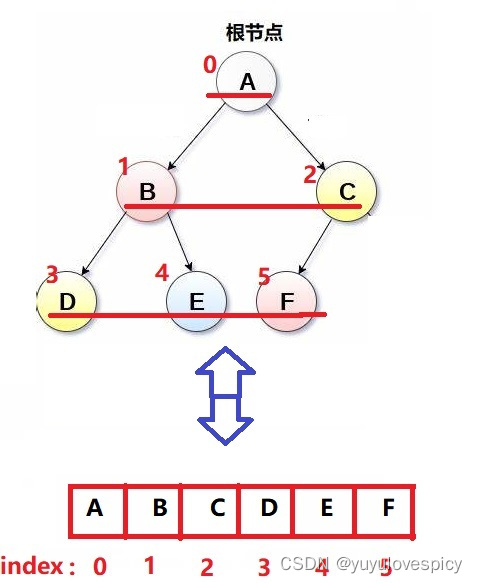
从上面，我们知道，只要你知道了一个节点在数组中存储的下标，那你就可以直接锁定这个节点的父亲，左孩子，右孩子，的存储下标。这也进一步说明我们用一个数组来表示完全二叉树的合理！！！

堆这个数据结构就是一棵完全二叉树，所以我们也是以这样，即数组的方式代表存储一个堆。

3. 堆的基本概念

3.1 堆的核心性质

堆，是一种特殊的完全二叉树，是一种非常实用的数据结构，跟进程地址空间的堆区没有任何的关系。

堆，分为大堆和小堆，大堆和小堆是相互反着的。

大堆永远保持：上面的父节点大于下面的左右孩子节点，即每一对“三角关系”：父亲 左孩子 右孩子，都满足，父亲 > 左孩子 && 父亲 > 右孩子。上克下。

小堆永远保持：上面的父节点小于下面的左右孩子节点，即每一对“三角关系”：父亲 左孩子 右孩子，都满足，父亲 < 左孩子 && 父亲 < 右孩子。下克上。

只要满足上述关系的完全二叉树，你就是堆。

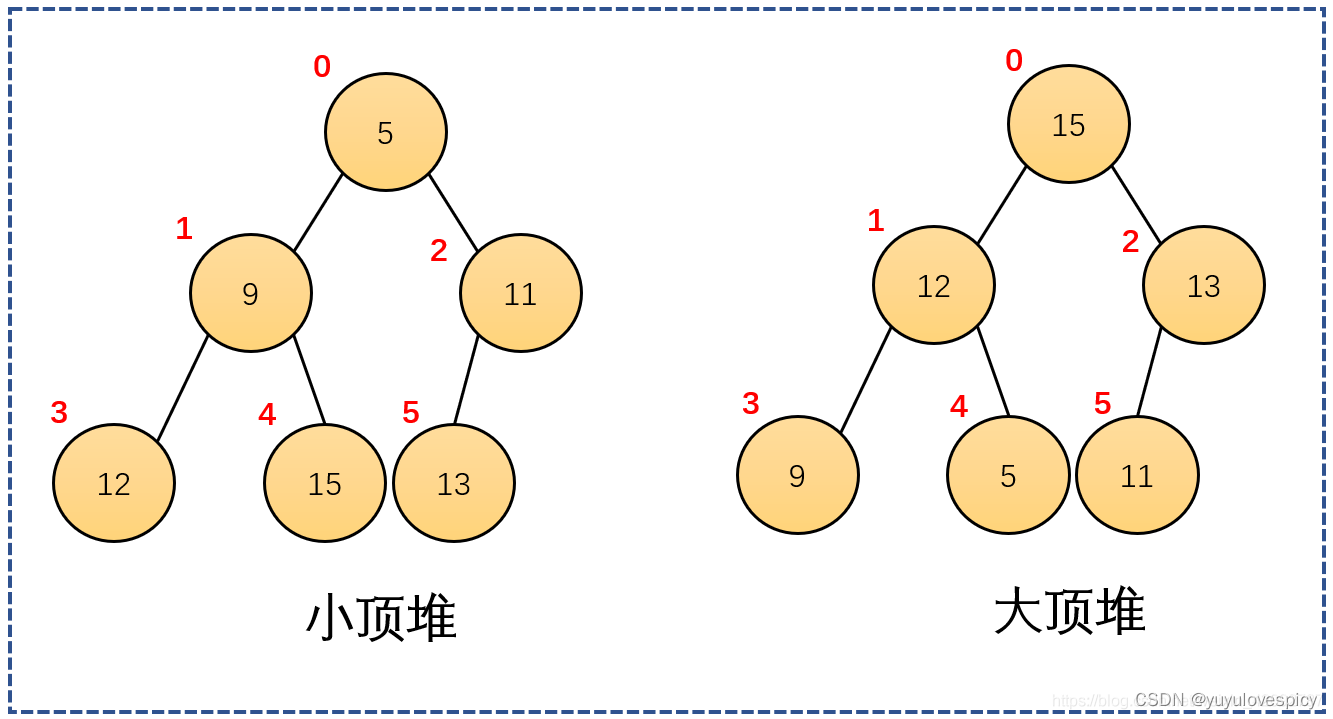
 如图，大堆，15节点的左右孩子12 13都是小于父亲15的；12节点的左右孩子9  5都是小于父亲12的；3节点的左孩子11，也是小于父亲13的。

同时，既然所有的三角关系都满足上述性质，那么其实你单拎出来任何一棵大堆/小堆的子树（注意拎出来的一棵完全二叉树），那么其实这棵子树也必然是大堆/小堆。

3.2 堆顶的性质

这里我们可以看到一个很明显的结论，大堆的根节点，我们称之为堆顶，永远是所有节点当中最大的。这是因为堆顶大于其左右孩子，而这左右孩子又继续作为父亲，继续往下扩散，继续大于他的左右孩子，这样依次往下扩散，我们很容易得出大堆堆顶的数据就是最大的。

同理，我们知道，小堆的堆顶，也永远是所有节点当中最小的。

3.3 堆的单支性质

根据堆的基本三角关系性质，然后我们又可以得出一个结论，在大堆当中，一个单支当中，上面的永远大于下面的，类比现实就是太太太爷爷永远比太太爷爷大，太太爷爷永远比太爷爷大，太爷爷永远比爷爷大，爷爷比爸爸大。

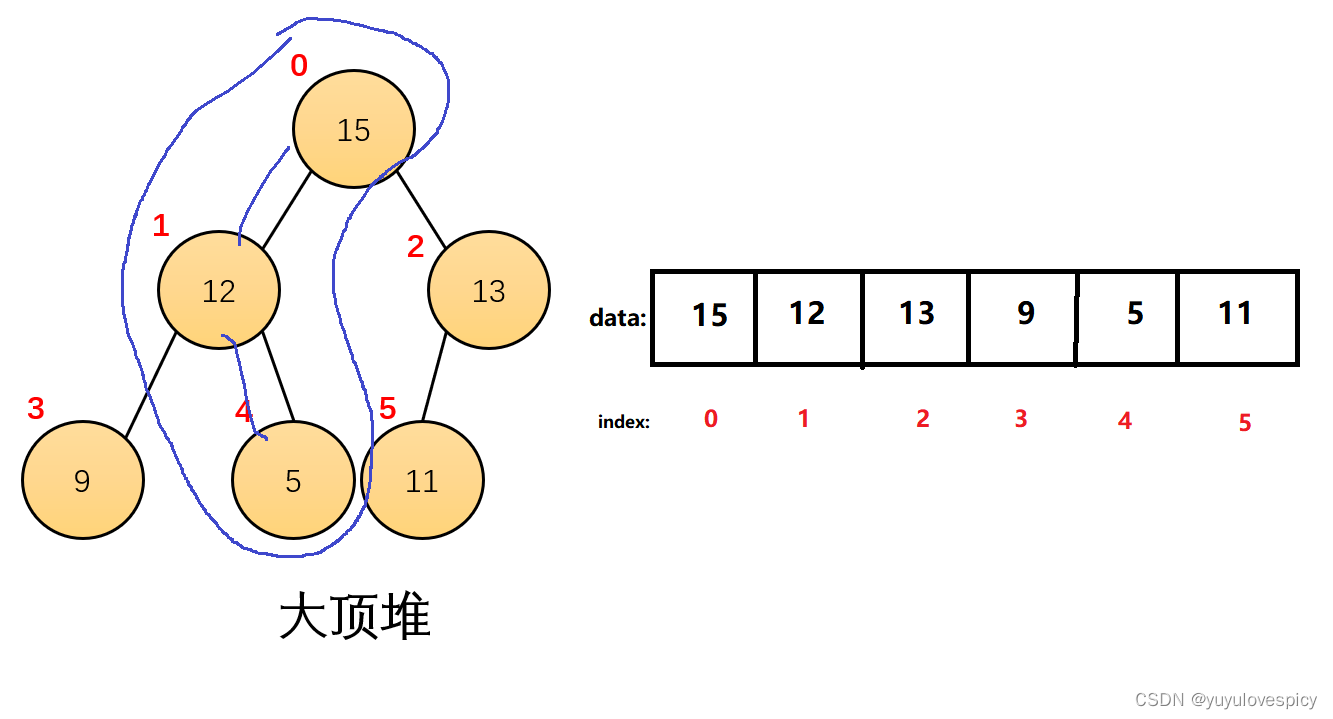
 同理在小堆的任何一个单支当中，上面的永远小于下面的。

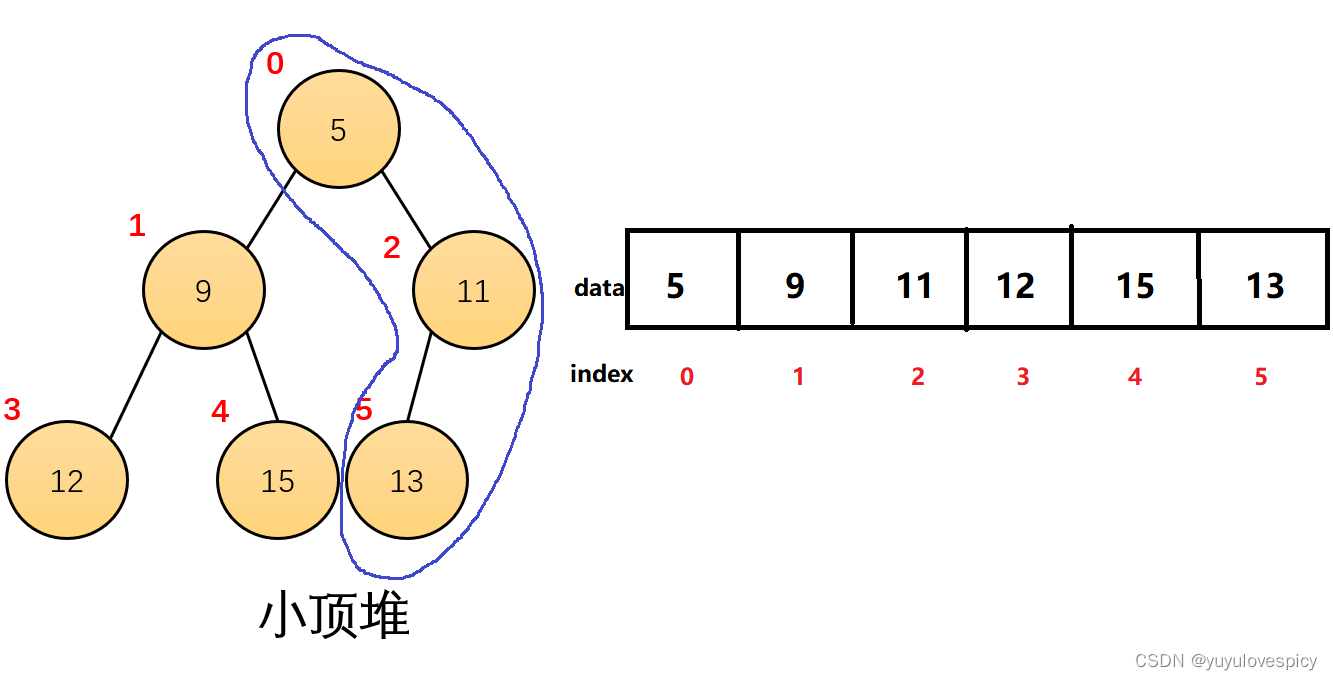
3.4 堆的左右支关系

 刚才我们看的都是同一支的上下节点的关系，那同层的左右的节点之间的大小对比关系呢？答：没有任何关系，同层的左右节点之间的大小，左节点大还是右节点大，这个是不确定事件。即同级别的分支和分支之间的大小之间没有任何的关系。如果非要说关系，那就是他们这些左右支里的值都比根小，但是事实上，左右支的大小对比关系，就是没有关系。

如下图中的左右支，这两个支没有大小对比关系。因为我们可以把12节点 和 13节点，直接交换位置，那么这其实也是一个大堆，大小对比关系都是不定的！

4.  用代码实现堆

4.1 堆类的实现

我们如何封装表示一个堆呢？事实上，堆这个完全二叉树，我们是用数组结构来实现的，所以我们可以直接封装一个数组就可以了。但是这样就是定长的了，不能够进行动态的增长，所以说我们不选择定义一个静态的数组int a[N]。而是封装一个顺序表即可！(1条消息) 数据结构的起航，用C语言实现一个简约却不简单的顺序表！（零基础也能看懂）_yuyulovespicy的博客-CSDN博客

//范式类型
typedef int HPDataType;
//实现堆（一种完全二叉树，节点在逻辑上一定是连续的），我们采用数组结构进行存储表示比较合适。
typedef struct Heap {
	HPDataType* _a; //数组-存储基本节点
	int _size;		//元素节点个数
	int _capacity;	//数组容量
}Heap;

我们的堆的相关接口，必须要传入的是Heap对象的指针，因为C语言，我们函数进行传参都是传值传参，我们传入的都是传入对象的拷贝！！！

4.2  堆的初始化

在一开始定义出来这个struct Heap对象的时候，它的内部的成员变量，都是随机值，_a是野指针，_size，_capacity都是随机值。所以我们必须要创建一个堆对象之后，就要完成堆的初始化。

void HeapInit(Heap* ph)
{
	//传入有效堆实体(指针非空)
	assert(ph);
	ph->_a = NULL;
	ph->_size = ph->_capacity = 0;
}

4.3 堆的销毁

我们创建一个堆，是在堆区开辟了连续的物理空间，申请的堆区空间需要我们主动释放，不然就会导致内存泄漏。所以在进程退出之前，我们必须要清理这个堆对象的资源。

void HeapDestroy(Heap* ph)
{
	//传入有效堆实体(指针非空)
	assert(ph);
	//释放所有堆区空间
	free(ph->_a);
	//置空内部
	ph->_a = NULL;
	ph->_size = ph->_capacity = 0;
	//外部置空ph
}

但是这里，我们传入的是这个Heap对象的指针的拷贝！并不是Heap对象指针实体。所以这里我们需要在外部对这个Heap对象指针实体进行主动的置空。

4.4 获取堆顶的数据

我们的堆，是一棵完全二叉树，并按照数组结构进行依次存储的。

 所以我们可以很容易知道，堆顶的数据，就是根节点，它在数组当中的存储下标就是index=0处的位置。

这里我们进一步强调堆顶的数据的重要性：根据我们的刚刚讨论的堆顶的性质，大堆的堆顶是所有元素当中的最大值，小堆的堆顶是所有元素当中的最小值，所以实际上堆顶代表着这整个堆的“脸面”，我们后面的TOPK问题就是通过堆顶来进行实现的。

HPDataType HeapTop(Heap* ph)
{
	//传入有效堆实体(指针非空)
	assert(ph);
	//非空有有效数据才可以返回
	assert(ph->_size > 0);
	//返回栈顶元素
	return ph->_a[0];
}

4.5 堆判空

我们的这个对是以顺序表进行架构的，这个_size成员的大小就代表了这个顺序表的数据个数，所以判堆是否为空，直接返回_size==0即可。

bool HeapEmpty(Heap* ph)
{
	return ph->_size == 0;
}

4.6 堆的大小

即返回当前堆，即完全二叉树的有效数据的个数。

int HeapSize(Heap* ph)
{
	assert(ph);
	return ph->_size;
}

4.7 堆内元素的交换

就是交换堆内的两个有效数据，我们这里实现出来，后面的向上调整/向下调整，会有大用。

void Swap(HPDataType* pa, HPDataType* pb)
{
	//交换两个元素的大小
	HPDataType tmp = *pa;
	*pa = *pb;
	*pb = tmp;
}

4.8* 堆的插入

4.8.1 问题引入

我们可以往堆里直接插入一共新元素，我们的堆首先是一棵完全二叉树，所有的数据不能有跳跃间隔，故我们的插入不能随便找一个空位置插入，应该所有的元素紧凑连接起来，所以现在插入的位置就先在尾插入了，如果我们直接尾插，那么就会变成下面这样：

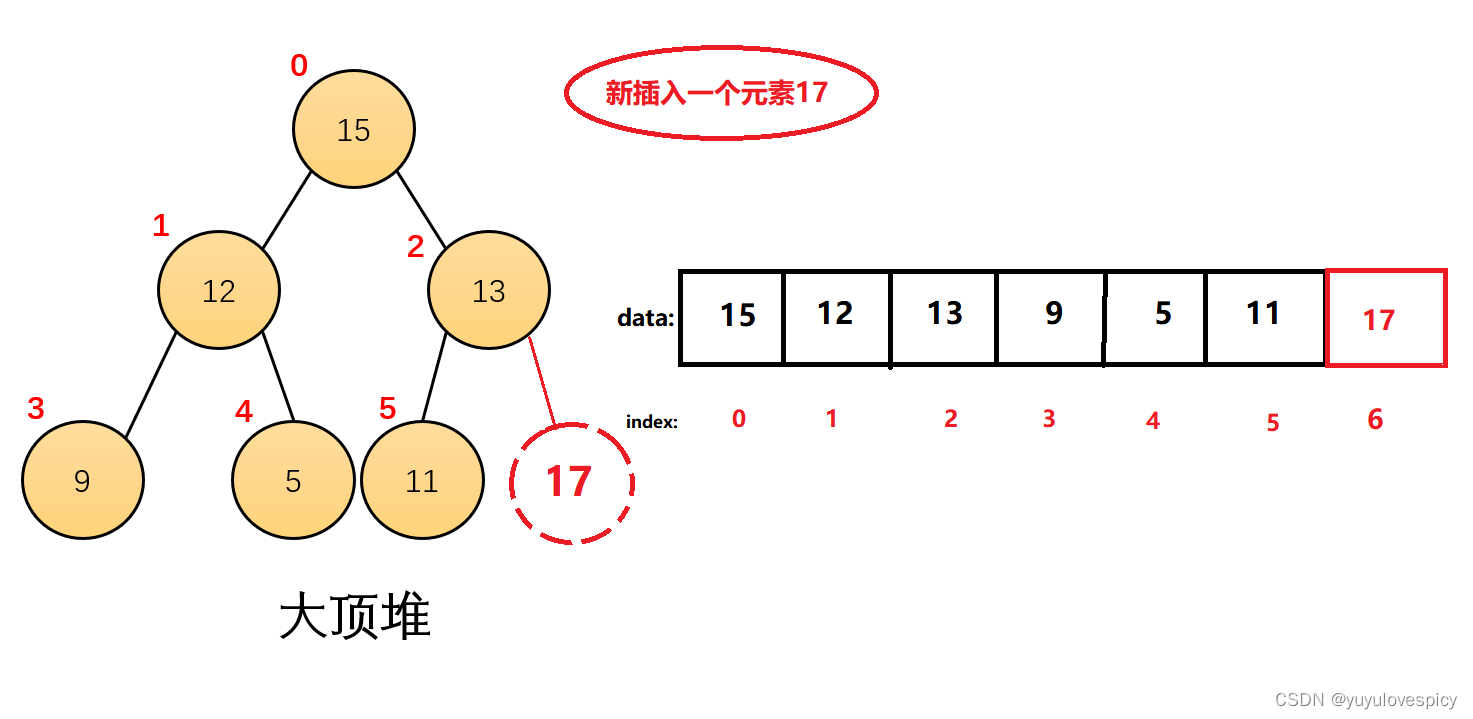
 现在这个大堆，就不再是大堆了！大堆中，所有的三角关系，都是父亲大于左右孩子，而我们新插入的17这个节点元素，就会导致不再满足大堆的性质了。父亲13不再大于孩子17了。

我们出现问题的点就在于这个17的位置是不合法的。所以说我们接下来所做的应该是调整这个17的位置，使得这个大堆，还满足大堆的性质。这就是我们堆中的AdjustUp向上调整！

4.8.2* 向上调整

大堆满足的是一个上下分支，上面的节点数据大于下面的节点数据；同级的左右分支之间，大小是没有关系。我们AdjustUp向上调整，所针对的对象，是这个新插入节点往上到根的这个上下分支（如下图圈中的分支）。

 我们向上调整的逻辑过程是：如果我child比parent更大，那child和parent的值就交换，把child这个大值交换上去，然后继续循环迭代；如果我child比parent更小，那就停止迭代循环，向上调整更新完成。

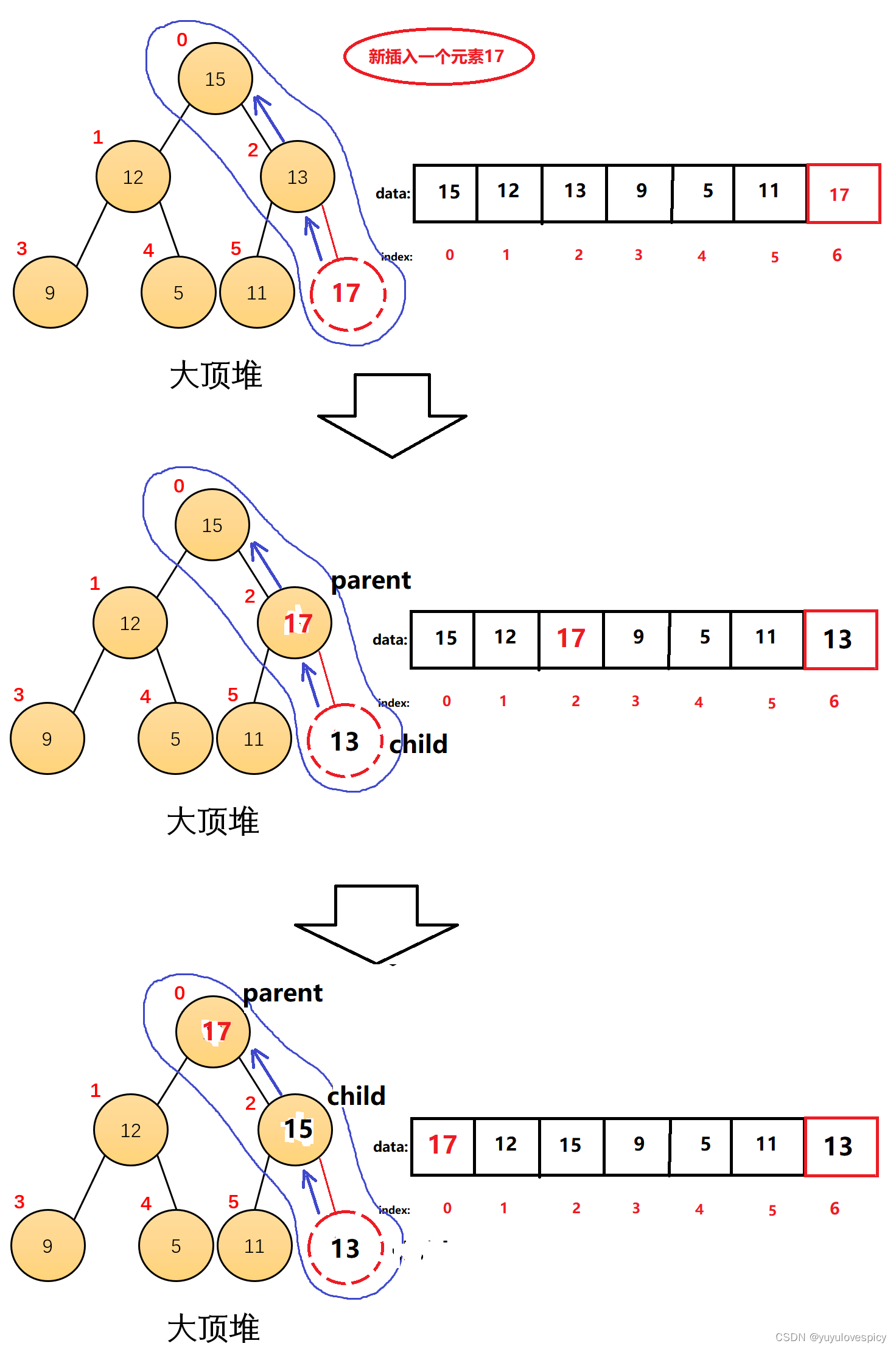
 我们根据思路得出代码:

然后我们再结合的数组结构实现的完全二叉树的结构,知道如何从父亲节点下标到左右孩子节点下标的转变，以及如何从左右孩子下标到父亲节点下标的转变。

//在完全二叉树a中,对pos位置的元素进行向上调整 为堆
void AdjustUp(int* a, int pos)
{
	assert(a);
	assert(pos >= 0);
	//完全二叉树(堆)中,parent=(child-1)/2,left_child=parent*2+1,right_child=parent*2+2 
	int child = pos;
	int parent = (child - 1) / 2;
	//向上调整的最坏情况是从pos尾调整到root[0]才调整完毕,即child[pos,0)
	while (child > 0)
	{
		//小堆调整主要使用<，大堆调整主要使用>。(统一用小堆实现)
		//小者往上调整
		if (a[child] < a[parent])
		{
			Swap(a + child, a + parent);
		}
		else //大小结构合理,调整完毕
		{
			break;
		}
		//往上层更新迭代父子
		child = parent;
		parent = (child - 1) / 2;
	}
}

4.8.3 堆插入的代码

所以堆的插入代码就很简单，就是插入之后，对这个新插入的节点进行向上调整。（当然啦，插入就要涉及扩容，所以我们需要检查扩容）。

void HeapPush(Heap* ph, HPDataType x)
{
	//传入有效堆实体(指针非空)
	assert(ph);
	//检查扩容
	if (ph->_size == ph->_capacity)
	{
		int newcapacity = (ph->_capacity == 0) ? 8 : ph->_capacity * 2;
		//扩容
		HPDataType* ptmp = (HPDataType*)realloc(ph->_a,sizeof(HPDataType) * newcapacity);
		if (ptmp == NULL)
		{
			perror("realloc");
			exit(1);
		}
		ph->_a = ptmp;
		ph->_capacity = newcapacity;
	}
	//先进行尾插
	ph->_a[ph->_size] = x;
	ph->_size++;
	//对尾插的数据进行向上调整
	AdjustUp(ph->_a, ph->_size-1);
}

4.9* 堆的删除

4.9.1 情景引入

堆的删除，是删除堆顶节点。可是我们不能直接删除堆顶的数据，因为我们既要维持完全二叉树的结构（即在数组存储上是连续的没有间隔的），同时我们也要维持堆的性质：父亲大于左右孩子 / 父亲小于左右孩子 的关系。

我们不能直接删除堆顶的数据，因为堆顶的数据的下标是[0]，我们使用的是数组形式组织的完全二叉树，直接头删就是O（N）的时间复杂度，效率过低。但是顺序表的尾删效率是极高的O（1）。

所以说，堆，采用的是替换法删除，我们是把要删除的堆顶节点数据，与该完全二叉树的最后一个节点的数据进行交换，然后我们直接删除最后一个节点即可。这样我们就的确删除了这个堆顶数据15。

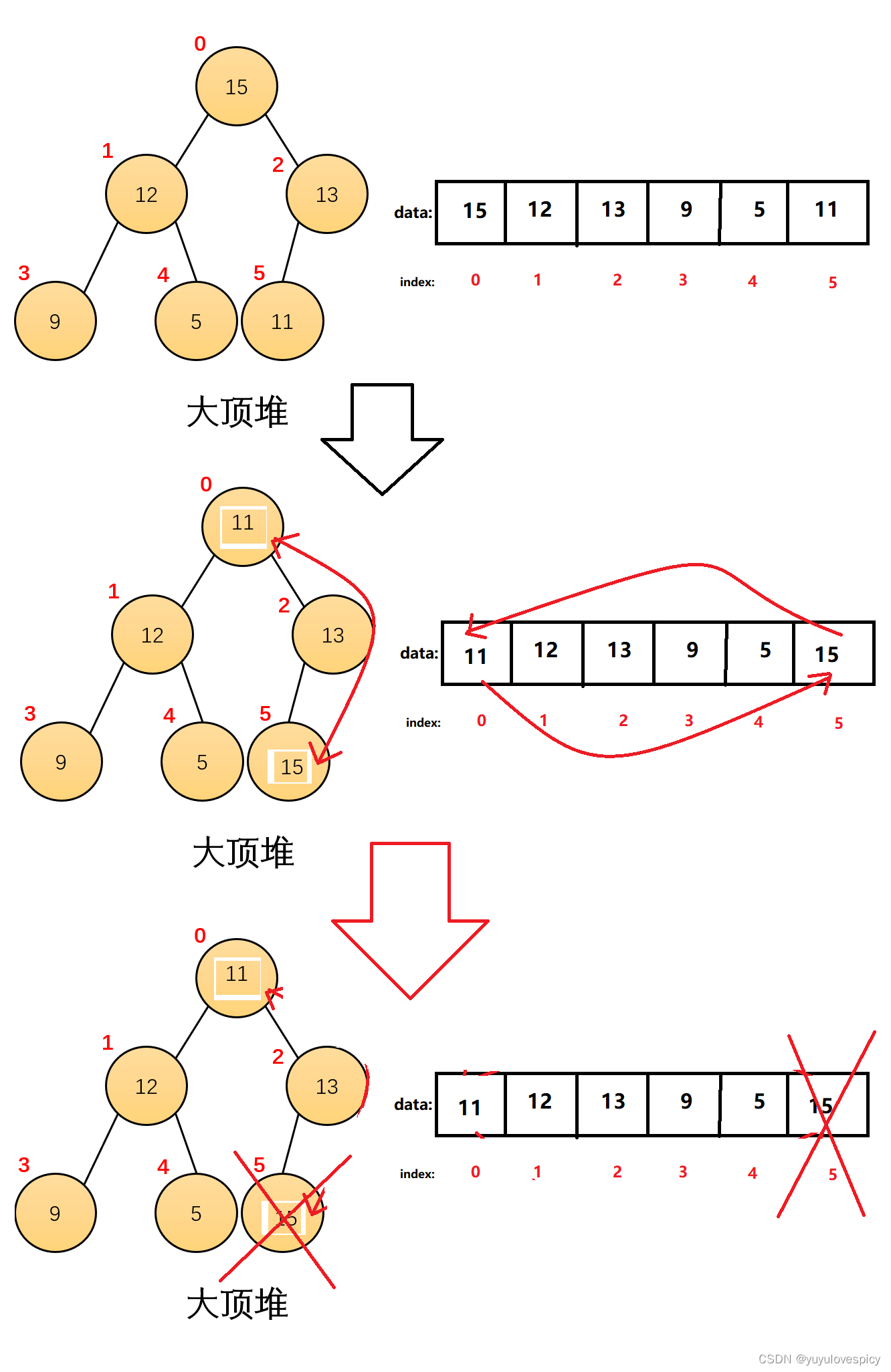
 然后使用这个但是删除之后呢？删除之后，虽然还是一棵完全二叉树，但是就不再是一个堆了！如图中，现在大堆顶替换成了11，而堆顶的左右孩子是12，13，大堆的parent（11）居然是小于下面的左右孩子12，13。这肯定是不对的，所以这里我们就请出AdjustDown向下调整来解决这个问题。

4.9.2* 向下调整

对于大堆来说，向下调整的思路就是：在这个parent，leftchild，rightchild这个三角关系当中，我们向下调整肯定是让这三角当中的最大值作为parent，两个较小值作为左右孩子child。

所以我们第一步是选取左右孩子当中的较大值节点child，当然也存在右孩子不存在的情况，我们需要特殊讨论，当然有不存在左右孩子的情况，那就说明我们已经向下调整到底，即调整完毕了。

第二步是，将parent和选出来的较大的child孩子，进行比较：如果child大孩子比parent父亲还大，那么我们就交换大孩子child和parent父亲的值，完成一次向下调整，然后继续迭代向下。而如果child大孩子比parent父亲还小，也即parent更大，符合大堆性质，那此时就调整结束。

 所以就产生代码：

//对pos位置的元素 在大小为sz的完全二叉树a中向下调整 为堆
void AdjustDown(int* a, int sz, int pos)
{
	assert(a);
	//小堆调整主要使用<，大堆调整主要使用>。(统一用小堆实现)
	/*parent向下调整,把parent child_left child_right中最小的放在parent的位置，发生交换则继续向下调整直至到最后一层*/
	int parent = pos;
	//使用child首先默认表示左孩子
	int child = parent * 2 + 1;
	//调整到最后一层停止向下调整
	while (child <= sz - 1)
	{
		//找出左右孩子中较小<的孩子去交换调整(当然首先右孩子要存在)
		if ((child + 1) <= sz - 1 && a[child + 1] < a[child])
		{
			//此时child代表右孩子去交换
			++child;
		}
		//如果parent小于<其中孩子，为了维护小堆结构需交换继续向下调整
		if (a[child] < a[parent])
		{
			Swap(a + parent, a + child);
		}
		else //parent可以作为左右孩子父亲，大小结构合理，则停止调整。
		{
			break;
		}
		//继续向下迭代
		parent = child;
		child = parent * 2 + 1;
	}
}

4.9.3 堆的删除代码实现

按照我们刚刚的思路，先替换法删除，然后，对新的换到堆顶的数据进行向下调整。

void HeapPop(Heap* ph)
{
	//传入有效堆实体(指针非空)
	assert(ph);
	//有有效数据存在才可以删除
	assert(!HeapEmpty(ph));
	/*栈的删除是对栈顶元素a[0]的删除*/
	//采用首尾置换删除法
	//1.交换首尾元素,删除尾部
	ph->_a[0] = ph->_a[ph->_size - 1];
	ph->_size--;
	//2.对新栈顶数据进行向下调整
	AdjustDown(ph->_a, ph->_size, 0);
}