note
- 基于图同构网络(GIN)的图表征网络。为了得到图表征首先需要做节点表征,然后做图读出。GIN中节点表征的计算遵循WL Test算法中节点标签的更新方法,因此它的上界是WL Test算法。
在图读出中,我们对所有的节点表征(加权,如果用Attention的话)求和,这会造成节点分布信息的丢失。 - 为了研究图神经网络的表达力问题,产生一个重要模型——图同构模型,
Weisfeiler-Lehman测试就是检测两个图是否在拓扑结构上图同构的近似方法;该测试最大的特点是:对每个节点的子树的聚合函数采用的是单射(Injective)的散列函数。
——由该特点我们可以通过设计一个单射聚合聚合函数来设计与WL一样强大的图卷积网络(同时,图同构网络有强大的图区分能力,适合图分类任务)。
文章目录
- note
- 零、Recap部分
- 一、GIN图同构网络
- 1.1 WL Graph Kernel
- 1.2 基于图同构网络(GIN)的图表征网络的实现
- 1.基于图同构网络的图表征模块(GINGraphRepr Module)
- 图表征模块运行流程
- 2.基于图同构网络的节点嵌入模块(GINNodeEmbedding Module)
- 3.GINConv--图同构卷积层
- 4.AtomEncoder 与 BondEncoder
- 1.3 The power of pooling
- 1.4 dgl中的GIN层代码
- 二、Expressive of Power GNNs
- 1.Motivation
- 2.文章内容
- 3.背景:Weisfeiler-Lehman Test (WL Test)
- (1)图同构性测试算法WL Test
- 背景介绍
- WL举例说明(以一维为栗子)
- 第一步:聚合
- 第二步:标签散列(哈希)
- 注:怎样的聚合函数是一个单射函数?
- 第三步:给节点重新打上标签。
- 第四步:数标签
- 第五步:判断同构性
- (2)WL Subtree Kernel图相似性评估(定量化)
- 4.小结
- 三、General Tips
- 附:时间安排
- Reference
零、Recap部分
一、GIN图同构网络
1.1 WL Graph Kernel
对节点颜色进行更新:
c
(
k
+
1
)
(
v
)
=
HASH
(
c
(
k
)
(
v
)
,
{
c
(
k
)
(
u
)
}
u
∈
N
(
v
)
)
c^{(k+1)}(v)=\operatorname{HASH}\left(c^{(k)}(v),\left\{c^{(k)}(u)\right\}_{u \in N(v)}\right)
c(k+1)(v)=HASH(c(k)(v),{c(k)(u)}u∈N(v))
1.2 基于图同构网络(GIN)的图表征网络的实现
基于图同构网络的图表征学习主要包含以下两个过程:
- 首先计算得到节点表征;
- 其次对图上各个节点的表征做图池化(Graph Pooling),或称为图读出(Graph Readout),得到图的表征(Graph Representation)。
自顶向下的学习顺序:GIN图表征—>节点表征
1.基于图同构网络的图表征模块(GINGraphRepr Module)
GIN图同构网络模型的构建
- 能实现判断图同构性的图神经网络需要满足,只在两个节点自身标签一样且它们的邻接节点一样时,图神经网络将这两个节点映射到相同的表征,即映射是单射性的。
- 可重复集合/多重集(Multisets):元素可重复的集合,元素在集合中没有顺序关系 。一个节点的所有邻接节点是一个可重复集合,一个节点可以有重复的邻接节点,邻接节点没有顺序关系。因此GIN模型中生成节点表征的方法遵循WL Test算法更新节点标签的过程。
在生成节点的表征后仍需要执行图池化(或称为图读出)操作得到图表征,最简单的图读出操作是做求和。由于每一层的节点表征都可能是重要的,因此在图同构网络中,不同层的节点表征在求和后被拼接,其数学定义如下,
h
G
=
CONCAT
(
READOUT
(
{
h
v
(
k
)
∣
v
∈
G
}
)
∣
k
=
0
,
1
,
⋯
,
K
)
h_{G} = \text{CONCAT}(\text{READOUT}\left(\{h_{v}^{(k)}|v\in G\}\right)|k=0,1,\cdots, K)
hG=CONCAT(READOUT({hv(k)∣v∈G})∣k=0,1,⋯,K)
采用拼接而不是相加的原因在于不同层节点的表征属于不同的特征空间。未做严格的证明,这样得到的图的表示与WL Subtree Kernel得到的图的表征是等价的。
图表征模块运行流程
(1)首先采用GINNodeEmbedding模块对图上每一个节点做节点嵌入(Node Embedding),得到节点表征;
(2)然后对节点表征做图池化得到图的表征;
(3)最后用一层线性变换对图表征转换为对图的预测。
2.基于图同构网络的节点嵌入模块(GINNodeEmbedding Module)
此节点嵌入模块基于多层GINConv实现结点嵌入的计算。此处我们先忽略GINConv的实现。输入到此节点嵌入模块的节点属性为类别型向量,

3.GINConv–图同构卷积层
图同构卷积层的数学定义如下:
x
i
′
=
h
Θ
(
(
1
+
ϵ
)
⋅
x
i
+
∑
j
∈
N
(
i
)
x
j
)
\mathbf{x}^{\prime}_i = h_{\mathbf{\Theta}} \left( (1 + \epsilon) \cdot \mathbf{x}_i + \sum_{j \in \mathcal{N}(i)} \mathbf{x}_j \right)
xi′=hΘ
(1+ϵ)⋅xi+j∈N(i)∑xj
由于输入的边属性为类别型,因此我们需要先将类别型边属性转换为边表征。我们定义的GINConv模块遵循“消息传递、消息聚合、消息更新”这一过程。
4.AtomEncoder 与 BondEncoder
由于在当前的例子中,节点(原子)和边(化学键)的属性都为离散值,它们属于不同的空间,无法直接将它们融合在一起。通过嵌入(Embedding),我们可以将节点属性和边属性分别映射到一个新的空间,在这个新的空间中,我们就可以对节点和边进行信息融合。
1.3 The power of pooling
- use element-wise sum pooling, instead of mean-/max-pooling
1.4 dgl中的GIN层代码
dgl的GINConv层:在这里插入代码片
"""Torch Module for Graph Isomorphism Network layer"""
# pylint: disable= no-member, arguments-differ, invalid-name
import torch as th
from torch import nn
from .... import function as fn
from ....utils import expand_as_pair
class GINConv(nn.Module):
def __init__(self,
apply_func,
aggregator_type,
init_eps=0,
learn_eps=False):
super(GINConv, self).__init__()
self.apply_func = apply_func
self._aggregator_type = aggregator_type
if aggregator_type == 'sum':
self._reducer = fn.sum
elif aggregator_type == 'max':
self._reducer = fn.max
elif aggregator_type == 'mean':
self._reducer = fn.mean
else:
raise KeyError('Aggregator type {} not recognized.'.format(aggregator_type))
# to specify whether eps is trainable or not.
if learn_eps:
self.eps = th.nn.Parameter(th.FloatTensor([init_eps]))
else:
self.register_buffer('eps', th.FloatTensor([init_eps]))
def forward(self, graph, feat, edge_weight=None):
r"""
Description
-----------
Compute Graph Isomorphism Network layer.
Parameters
----------
graph : DGLGraph
The graph.
feat : torch.Tensor or pair of torch.Tensor
If a torch.Tensor is given, the input feature of shape :math:`(N, D_{in})` where
:math:`D_{in}` is size of input feature, :math:`N` is the number of nodes.
If a pair of torch.Tensor is given, the pair must contain two tensors of shape
:math:`(N_{in}, D_{in})` and :math:`(N_{out}, D_{in})`.
If ``apply_func`` is not None, :math:`D_{in}` should
fit the input dimensionality requirement of ``apply_func``.
edge_weight : torch.Tensor, optional
Optional tensor on the edge. If given, the convolution will weight
with regard to the message.
Returns
-------
torch.Tensor
The output feature of shape :math:`(N, D_{out})` where
:math:`D_{out}` is the output dimensionality of ``apply_func``.
If ``apply_func`` is None, :math:`D_{out}` should be the same
as input dimensionality.
"""
with graph.local_scope():
aggregate_fn = fn.copy_src('h', 'm')
if edge_weight is not None:
assert edge_weight.shape[0] == graph.number_of_edges()
graph.edata['_edge_weight'] = edge_weight
# message function
aggregate_fn = fn.u_mul_e('h', '_edge_weight', 'm')
feat_src, feat_dst = expand_as_pair(feat, graph)
graph.srcdata['h'] = feat_src
# aggregate function: neighbor info + self info
graph.update_all(aggregate_fn, self._reducer('m', 'neigh'))
# self info
rst = (1 + self.eps) * feat_dst + graph.dstdata['neigh']
if self.apply_func is not None:
rst = self.apply_func(rst)
return rst
二、Expressive of Power GNNs

提出图同构网络的论文:How Powerful are Graph Neural Networks?
1.Motivation
新的图神经网络的设计大多基于经验性的直觉、启发式的方法和实验性的试错。人们对图神经网络的特性和局限性了解甚少,对图神经网络的表征能力学习的正式分析也很有限。
2.文章内容
- (理论上)图神经网络在区分图结构方面最高能达到与WL Test一样的能力。
- 确定了邻接节点聚合方法和图池化方法应具备的条件,在这些条件下,所产生的图神经网络能达到与WL Test一样的能力。
- 分析过去流行的图神经网络变体(如GCN和GraphSAGE)无法区分一些结构的图。
- 开发了一个简单的图神经网络模型–图同构网络(Graph Isomorphism Network, GIN),并证明其分辨同构图的能力和表示图的能力与WL Test相当。
3.背景:Weisfeiler-Lehman Test (WL Test)
(1)图同构性测试算法WL Test
背景介绍
两个图是同构的,意思是两个图拥有一样的拓扑结构,也就是说,我们可以通过重新标记节点从一个图转换到另外一个图。Weisfeiler-Lehman 图的同构性测试算法,简称WL Test,是一种用于测试两个图是否同构的算法。
WL Test 的一维形式,类似于图神经网络中的邻接节点聚合。WL Test
1)迭代地聚合节点及其邻接节点的标签,然后 2)将聚合的标签散列(hash)成新标签,该过程形式化为下方的公式,
L
u
h
←
hash
(
L
u
h
−
1
+
∑
v
∈
N
(
U
)
L
v
h
−
1
)
L^{h}_{u} \leftarrow \operatorname{hash}\left(L^{h-1}_{u} + \sum_{v \in \mathcal{N}(U)} L^{h-1}_{v}\right)
Luh←hash
Luh−1+v∈N(U)∑Lvh−1
符号:
L
u
h
L^{h}_{u}
Luh表示节点
u
u
u的第
h
h
h次迭代的标签,第
0
0
0次迭代的标签为节点原始标签。
在迭代过程中,发现两个图之间的节点的标签不同时,就可以确定这两个图是非同构的。需要注意的是节点标签可能的取值只能是有限个数。

WL举例说明(以一维为栗子)
给定两个图 G G G和 G ′ G^{\prime} G′,每个节点拥有标签(实际中,一些图没有节点标签,我们可以以节点的度作为标签)。
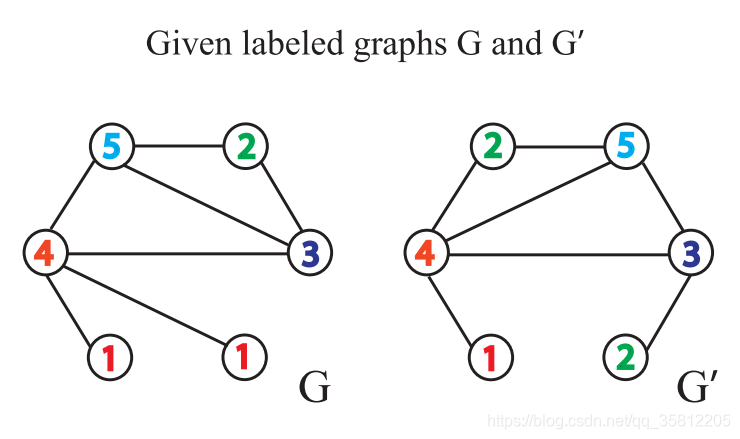
Weisfeiler-Leman Test 算法通过重复执行以下给节点打标签的过程来实现图是否同构的判断:
第一步:聚合
聚合自身与邻接节点的标签得到一串字符串,自身标签与邻接节点的标签中间用,分隔,邻接节点的标签按升序排序。排序的原因在于要保证单射性,即保证输出的结果不因邻接节点的顺序改变而改变。
如下图就是,每个节点有个一个label(此处表示节点的度)。

如下图,做标签的扩展:做一阶BFS,即只遍历自己的邻居,比如在下图中G中原5号节点变成(5,234),这是因为原(5)节点的一阶邻居有2、3、4。
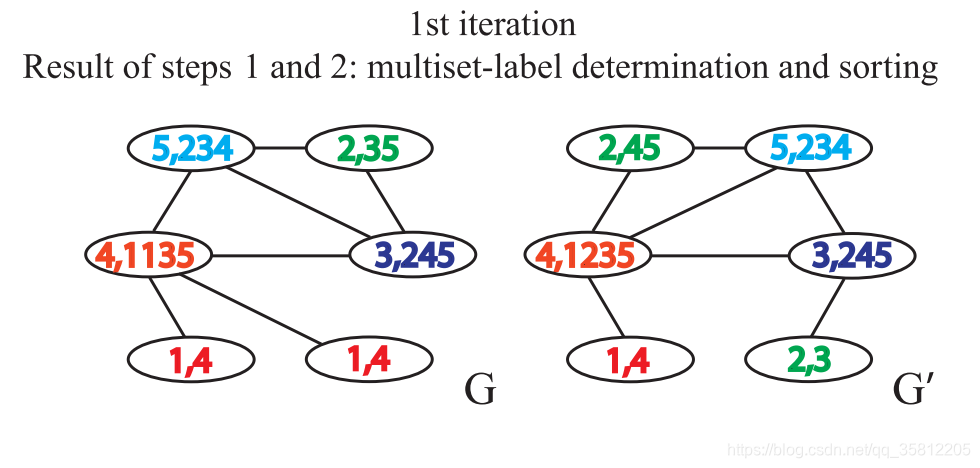
第二步:标签散列(哈希)
即标签压缩,将较长的字符串映射到一个简短的标签。
如下图,仅仅是把扩展标签映射成一个新标签,如5,234映射为13

注:怎样的聚合函数是一个单射函数?
什么是单射函数?
单射指不同的输入值一定会对应到不同的函数值。如果对于每一个y存在最多一个定义域内的x,有f(x)=y,则函数f被称为单射函数。
看一个栗子:
两个节点v1和v2,其中v1的邻接点是1个黄球和1个蓝球,v2的邻接点是2个邻接点是2个黄球和2个蓝球。最常用的聚合函数包含图卷积网络中所使用的均值聚合,以及GraphSAGE中常用的均值聚合或最大值聚合。
(1)如果使用均值聚合或者最大值聚合,聚合后v1的状态是(黄,蓝),而v2的状态也是(黄,蓝),显然它们把本应不同的2个节点映射到了同一个状态,这不满足单射的定义。
(2)如果使用求和函数,v1的状态是(黄,蓝),而v2的状态是(2×黄,2×蓝),也就分开了。

可以看出WL测试最大的特点是:对每个节点的子树的聚合函数采用的是单射(Injective)的散列函数。
第三步:给节点重新打上标签。
继续一开始的栗子,
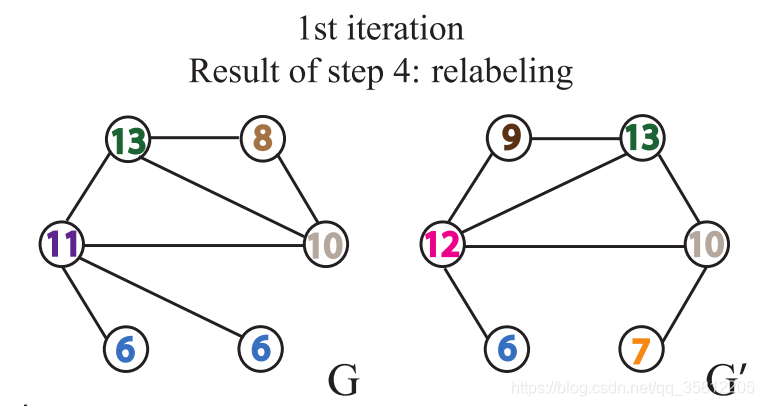
第四步:数标签
如下图,在G网络中,含有1号标签2个,那么第一个数字就是1。这些标签的个数作为整个网络的新特征。

每重复一次以上的过程,就完成一次节点自身标签与邻接节点标签的聚合。
第五步:判断同构性
当出现两个图相同节点标签的出现次数不一致时,即可判断两个图不相似。如果上述的步骤重复一定的次数后,没有发现有相同节点标签的出现次数不一致的情况,那么我们无法判断两个图是否同构。
当两个节点的 h h h层的标签一样时,表示分别以这两个节点为根节点的WL子树是一致的。WL子树与普通子树不同,WL子树包含重复的节点。下图展示了一棵以1节点为根节点高为2的WL子树。
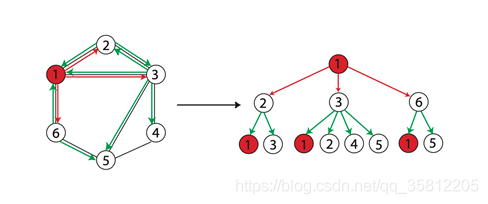
(2)WL Subtree Kernel图相似性评估(定量化)
此方法来自于Weisfeiler-Lehman Graph Kernels。
- WL测试不能保证对所有图都有效,特别是对于具有高度对称性的图,如链式图、完全图、环图和星图,它会判断错误。
- WL测试只能判断两个图的相似性,无法衡量图之间的相似性。要衡量两个图的相似性,我们用WL Subtree Kernel方法。
Weisfeiler-Lehman Graph Kernels 方法提出用WL子树核衡量图之间相似性。该方法使用WL Test不同迭代中的节点标签计数作为图的表征向量,它具有与WL Test相同的判别能力。在WL Test的第 k k k次迭代中,一个节点的标签代表了以该节点为根的高度为 k k k的子树结构。
该方法的思想是用WL Test算法得到节点的多层的标签,然后我们可以分别统计图中各类标签出现的次数,存于一个向量,这个向量可以作为图的表征。两个图的表征向量的内积,即可作为这两个图的相似性估计,内积越大表示相似性越高。

4.小结
大部分空域图神经网络的更新步骤,和WL测试非常类似。就像消息传递网络中归纳的框架,大部分基于空域的图神经网络都可以归结为2个步骤:聚合邻接点信息(aggregate),更新节点信息(combine)。
a
v
k
=
Aggregate
(
{
h
u
k
−
1
:
u
∈
N
(
v
)
}
)
,
h
v
k
=
Combine
(
h
v
k
−
1
,
a
v
k
)
a_{v}^{k}=\operatorname{Aggregate}\left(\left\{\boldsymbol{h}_{u}^{k-1}: u \in \mathcal{N}(v)\right\}\right), \boldsymbol{h}_{v}^{k}=\operatorname{Combine}\left(\boldsymbol{h}_{v}^{k-1}, \boldsymbol{a}_{v}^{k}\right)
avk=Aggregate({huk−1:u∈N(v)}),hvk=Combine(hvk−1,avk)
与WL测试一样,在表达网络结果时,一个节点的表征会由该结点的父结点的子树信息聚合而成。
正如上面提到的栗子中(下图),均值聚合或者最大值聚合把栗子中的v1和v2两个节点映射到了同一个状态(错误),而如果使用求和函数则能正确分开两者状态。WL测试最大的特点是:对每个节点的子树的聚合函数采用的是单射(Injective)的散列函数。
——由该特点我们可以通过设计一个单射聚合聚合函数来设计与WL一样强大的图卷积网络(同时,图同构网络有强大的图区分能力,适合图分类任务)。

三、General Tips

附:时间安排
| 任务 | 任务内容 | 截止时间 | 注意事项 |
|---|---|---|---|
| 2月11日开始 | |||
| task1 | 图机器学习导论 | 2月14日周二 | 完成 |
| task2 | 图的表示和特征工程 | 2月15、16日周四 | 完成 |
| task3 | NetworkX工具包实践 | 2月17、18日周六 | 完成 |
| task4 | 图嵌入表示 | 2月19、20日周一 | 完成 |
| task5 | deepwalk、Node2vec论文精读 | 2月21、22、23、24日周五 | 完成 |
| task6 | PageRank | 2月25、26日周日 | 完成 |
| task7 | 标签传播与节点分类 | 2月27、28日周二 | 完成 |
| task8 | 图神经网络基础 | 3月1、2日周四 | 完成 |
| task9 | 图神经网络的表示能力 | 3月3日周五 | 完成 |
| task10 | 图卷积神经网络GCN | 3月4日周六 | |
| task11 | 图神经网络GraphSAGE | 3月5日周七 | |
| task12 | 图神经网络GAT | 3月6日周一 |
Reference
[2] CS224W官网:https://web.stanford.edu/class/cs224w/index.html
[3] https://github.com/TommyZihao/zihao_course/tree/main/CS224W
[4] cs224w(图机器学习)2021冬季课程学习笔记11 Theory of Graph Neural Networks






![[AI助力] CS143学习笔记1](https://img-blog.csdnimg.cn/9fdaf39c2f2341fe97616eedf307cf90.png)