239. 滑动窗口最大值

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

输入：nums = [1], k = 1
输出：[1]

思路：单调队列

​ ⚜️其实这道题的解法有不同种形式，但是绕不开的就是使用单调队列的思想，为什么呢❓❓❓

​ 因为如果这个时候我们不用单调队列的话，就是说我们每次去控制这个窗口里面的最大值，如果这个窗口很大，那么时间复杂度是非常高的，因为遍历一遍这个窗口获取最大值的时间复杂度是 O(k)，而我们还得去遍历这个数组的元素，那么总和起来就是 O(n*k)，这样子在这道题是会超时的！所以我们得使用单调队列的思想！

​ 那么我们得先了解一下，什么是单调队列！

什么是单调队列

​ 单独队列本质还是一个队列，只是我们规定这个队列是一个单调递减或者单调递增队列！⚜️单调递减和递增是什么意思呢❓❓❓

​ 这里以单调递减为例，因为和我们这道题比较符合！我们举一个数学上面的例子 y = ax + b，我们知道递减就是函数在某个区间上面的 y 随着 x 的增大，而不断的减小或者相等，但是如果我们定义它为单调递减，那么这个函数则变成在 整个区间上面都是 y 随着 x 的增大而不断的减小！

​ 一般来说，单调队列使用 C++ 中的 deque 来实现会更好，因为其支持双端的插入删除以及获取双端元素！

​ ⚜️那么这道题要使用单调递减还是单调递增呢❓❓❓

​ 其实用单调递减会更加的符合滑动窗口的原理，我们保持从队头的元素开始，每个元素都大于其后面的元素，这样子像下图一样：

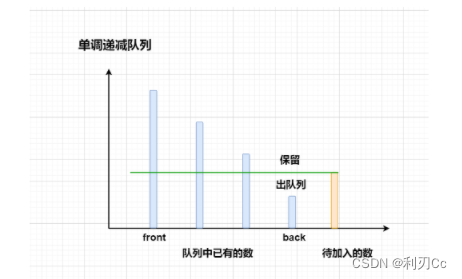
​ 也就是我们**保持让队头的元素是整个队列里面最大的**！

​ ⚜️这样子有什么好处呢❓❓❓

​ 我们每次取当前窗口的最大值，那么就和这个队头元素有关系啦，但是我们得来维护一下这个队列，而不同方式维护就有了不同的实现方法，下面我们举两种方法，其中我觉得最好理解的就是第一种！

1、队列维护数组下标

滑动窗口最大值 | 图解单调队列 | 最清晰易懂的讲解【c++/java】

​ ⚜️为什么要维护数组的下标呢❓❓❓

​ 因为每次我们需要去控制这个窗口移动，并保持让队列中的元素都落于这个窗口内，所以我们得一直关注着队列中的元素的值是在 nums 数组中的哪个位置，会不会出界，这些问题都要考虑，所以我们干脆直接用队列来保存其数组的下标，然后比较大小也是非常方便，因为是数组，所以有了下标，我们直接通过 nums[i] 就能快速索引到对应的元素，根本不用担心效率问题！并且这样子也非常的好控制！

​ 下面我们来看看具体的步骤（下面步骤中默认我们的队列变量名叫做dq）：

1. 遍历 nums 数组的每个元素
2. 每次遍历元素的时候，先循环判断一下队头元素在nums中位置是否已经掉出了窗口范围
   • 如果 i - k + 1 > dq.front()，说明队头元素已经不落在该窗口内了，我们就将队头pop掉！否则不用。
     • （值得解释一下的是这里的 i - k + 1 其实代表的就是窗口的第一个元素下标，也就是窗口的头位置！其中 dq.front() 代表的是队头元素在 nums 中的下标，如果我们的窗口头位置都超过了这个队头元素的下标了，那么说明这个队头元素不是当前窗口内的！）
     • （还有值得注意的是这里可以进行循环判断，也可以不进行循环判断，因为我们每次都只会对 i 进行一次的 ++，但是为了代码上面看起来严谨，可以将其改为循环判断！）
3. 控制新元素 nums[i] 加入的时候保持单调递减队列的规则
   • 如果 nums[i] > dq.back()，此时如果直接将 nums[i] 加入队列的话，会破坏单调递减的规则，所以我们要将 dq.back() 进行删除，并且不断循环判断，直到队列为空，或者遇到比 nums[i] 小或者等于的值为止！
4. 将 nums[i] 加入单调队列
5. 最后判断一下是否已经到了满足窗口大小 k 的位置了
   • 是的话则开始向数组 v 中 push 进每次窗口最大的元素，也就是队头元素在 nums 中对应位置的元素！

​ 💥**注意：队列中队头元素不一定是最大的，因为存放的不是数组中元素的值，而是其最大元素的下标！**

​ 其实这道题是相对比较复杂的，最好是自己先模拟这个过程！

​ 下面给出代码：

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        vector<int> v;
        deque<int> dq;
        for(int i = 0; i < nums.size(); ++i)
        {
            // 1、控制窗口的元素大小不大于k个，若大于则pop掉队头
            while(dq.size() > 0 && i - k + 1 > dq.front())
                dq.pop_front();
            
            // 2、控制新元素加入的时候保持单调递减队列的规则
            // 若新元素大于其队尾的元素，那么则pop掉该元素，直到遇到比新元素大或者相等为止
            while(dq.size() > 0 && nums[i] > nums[dq.back()])
                dq.pop_back();
            
            // 3、将新元素加入队列
            dq.push_back(i);
            
            // 4、若其循环到满足窗口大小k的位置了，则开始向v中push进每次最大的元素，也就是队头元素
            // 其中因为i是下标而k是大小，所以i要加一
            if(i + 1 >= k)
                v.push_back(nums[dq.front()]);
        }
        return v;
    }
};

2、队列维护数组元素值

[C++]滑动窗口最大值–单调队列

​ 这种方法可能是我们会比较先于维护数组下标而想到的，因为通常来说我们都会先去想怎么存放这个值，而不是存放对应下标，也确实，这道题如果是维护元素的值，那么相对于第一种方法来说会更容易出错一点，因为我们得去控制这个窗口移动的时候于队列元素的关系，保持其一直是窗口内有效元素！

​ 既然队列要维护数组元素值，那么当然队头元素就和第一种方法不一样了，这次队头元素肯定是队列里面最大的，因为这是一个单调队列，并且其存放的本身就是元素的值而不是下标！

​ 💥下面是步骤：

1. 首先可以维护队列保持单调递减，将 nums[i] 和队尾元素进行比较，若 dq.back() < nums[i] 说明需要 pop 掉队尾元素，和方法一类似！
2. 将新元素加入队列
3. 若其循环到满足窗口大小 k 的位置了，则开始向 v 中 push 进每次最大的元素，也就是队头元素，和方法一类似！
4. 注意还要维护队列元素是否在窗口内有效（因为要进行 nums 索引，所以最好放到第三步这个判断语句中比较安全）

​ 其实和第一种方法大同小异，不同的就是它们的大小判断等等，最重要的是这个第四步，也就是控制这个队列中队头等元素是否还在合法的窗口区间内，如果不是的话则要进行删除，而我们并不容易判断这个区间，因为我们怎么知道队头元素对应 nums 中的下标呢❓❓❓

​ 其实这就是一个难点，所以我们要改变思路：

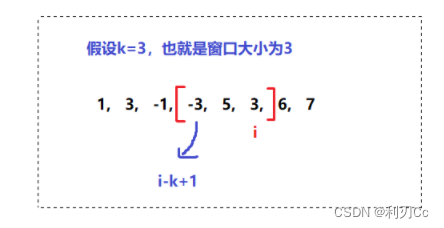
​ 💥因为每次我们只让 i 累加一次，也就是每次遍历只会让 i 向后走一步，那么我们只需要跟着遍历每次的窗口第一个元素，是否和当前队头的元素一样，一样的话说明遍历下一个元素的时候，这个元素就已经不再是窗口内的元素了，所以我们就把这个队头元素给 pop 掉！而这个窗口的头位置就是 i-k+1 处，但是由于窗口一开始还没达到 k 个，所以要建立在条件是 i+1 >= k 的基础之上！

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        vector<int> v;
        deque<int> dq;
        for(int i = 0; i < nums.size(); ++i)
        {
            // 1、首先可以维护队列保持单调递减，将nums[i]和队尾元素进行比较
            while(dq.size() > 0 && dq.back() < nums[i])
                dq.pop_back();
			
            // 2、将新元素加入队列
            dq.push_back(nums[i]);

            // 3、若其循环到满足窗口大小k的位置了，则开始向v中push进每次最大的元素，也就是队头元素
            // 其中因为i是下标而k是大小，所以i要加一
            if(i + 1 >= k)
            {
                v.push_back(dq.front());

                // 4、注意还要维护队列元素（因为要进行nums索引，所以最好放到if(i+1>=k)这个判断语句中比较安全）
                if(dq.size() > 0 && dq.front() == nums[i - k + 1])
                    dq.pop_front();
            }
        }
        return v;
    }
};