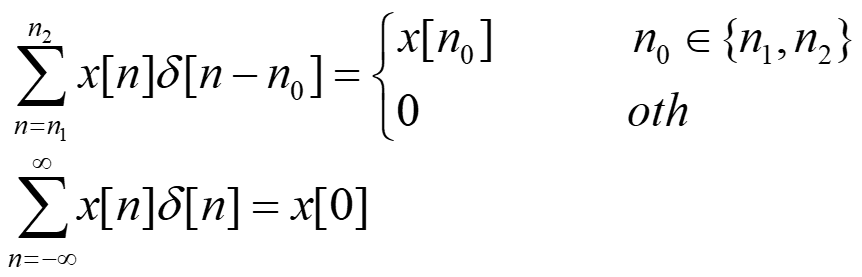Zhe Xu and Ufuk Topcu. 2019. Transfer of temporal logic formulas in reinforcement learning. In Proceedings of the 28th International Joint Conference on Artificial Intelligence (IJCAI’19). AAAI Press, 4010–4018.

这是一篇将inference和learning结合起来的文章，并且利用timed automata建立了比$\tau$-MDP 更高层的抽象。

文章内容：

1. 从轨迹中推理出MITL公式

2. 判断是否可以迁移

3. 对于原任务和目标任务，对每个子公式构建timed automaton

4. 原任务在构建的automaton上进行强化学习

5. 建立原任务和目标任务的映射，把Q表迁移至目标任务

6. 在迁移过来的Q表的基础上继续进行强化学习

结果：在两个相近的任务间进行迁移学习，采样效率最多能提高一个量级

---

1 Intro

高层信息的结合能够大大提高强化学习的采样效率

源任务：先去绿色区域待够4秒，再在40秒内到达黄色区域

目标任务：先去绿色区域待够5秒，再在40秒内到达黄色区域

机器人事先不知道绿色和黄色区域的位置

40秒时完成任务奖励100，否则惩罚-10

判断能否迁移：1. 没有相似性判断标准 2. 逻辑相似性是隐形的，要从数据中才能看出来 3. 没有自动化的迁移首端

---

2 前提

2.1 MITL

timed word: 一段轨迹，每个元素为当前时刻状态满足的原子命题的子集

“A timed word generated by a trajectory s0:L is defined as a sequence (L(st1 ), t1), . . . , (L(stm ), tm),” (Xu and Topcu, 2019, p. 4) (pdf)

timed word符合 $\Phi$=轨迹符合STL

2.2 Timed Automaton

$C$ clock variable

${\phi }_C$ clock constraints：时间的取值范围

Def. 1:

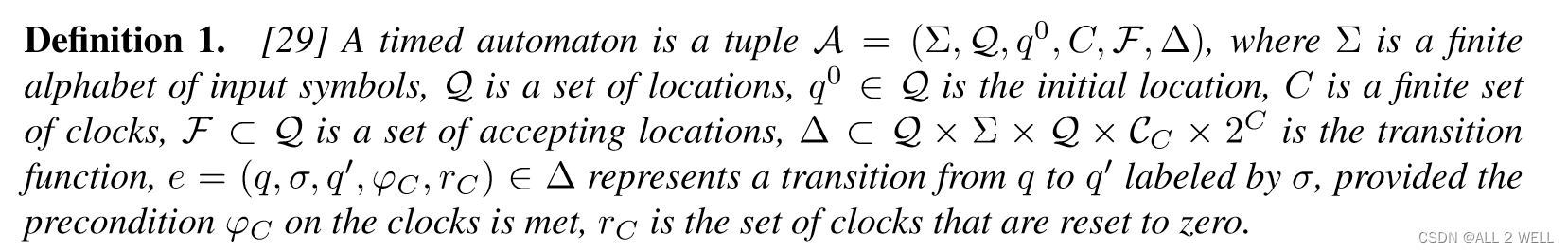
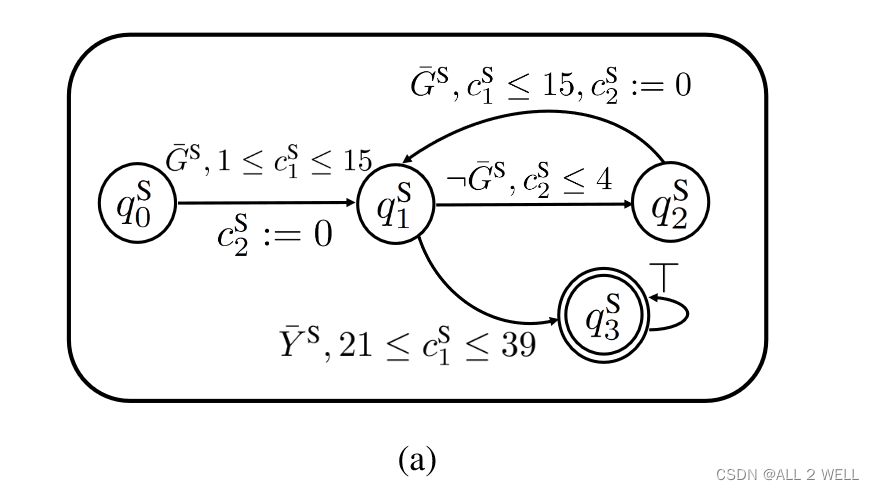
$\mathcal{A}$ timed automaton:

$\sigma \in \Sigma$ 输入

$q\in \mathcal{Q}$ 状态

${\phi }_C$ 到达的时钟条件

$r_C$ 被置零的时钟

$\mathcal{F}\subset \mathcal{Q}$ 接受状态：到达结束状态说明STL任务完成了

$\Delta$ 转移函数：到时间给定输入、位置，更新位置并且置零一批时钟

离散时间的timed Automata： 滴答自动机

$v$ clock valuation: 所有钟的时间构成一个向量

timed word 带时间戳的输入序列

a run （状态，时钟）序列

flow-step 由时间触发的

edge-step 由输入触发的

---

3 Inference

3.1 MITL信息增益

$G_L$ 长度为L的轨迹出现的概率分布

Def.2:

${\bar{G}}_L^{\varphi }$ 已知MITL公式的后验概率分布

Def.3:

定义信息增益为KL散度

3.2 问题陈述

考虑二阶以下的基本命题

Def.4

$t_S,t_e$: 衡量状态应该保存的大小

satisfying formula 满足最小正确分类率和公式长度的公式

Def.5

SDNF: 用于保证子公式的时间区间不重合，按照先后顺序排列

3.3 基于决策树的公式推理

${\Gamma }_z$ 参数的约束

用粒子群优化方法最大化信息增益I和正确分类率CR

Akra-Bazzi方法：计算复杂度

---

4 任务迁移

4.1 可迁移性定义

Def.5 结构等价性：逻辑结构相同、时序算子相同

Def.7 结构可迁移性的判断条件：

1. 结构等价

2. 或者每个子公式结构等价

data collection phase: 源任务和目标任务都收集一系列带标记的轨迹

Def. 8 逻辑可迁移性

1. 源任务和目标任务存在satisfying formula

2. 且两个satisfying formula集合中存在结构可迁移的公式

4.2 逻辑结构迁移：建立两个公式间的对应关系

1. 在源任务中提取公式，判断是否为satisfying formula

2. 在目标任务中提取公式：将原任务的结构作为公式模板，进行参数学习，判断是否为satisfying formula

3. 对目标任务的每个子任务构建DTA，在拓展的状态空间上用RL更新：

   • 每个子任务所对应的DTA的（智能体状态，DTA中的状态 ，时钟向量）

   • 每个回合根据启发式方法选取第i个子任务：子公式对应的原子命题的空间中心距离初始状态最近->即选择最容易完成的一个任务（由于初始位置是随机选定的，所以其他的任务也是可能会探索的？）

   • 用Q-learning进行Q表的更新

4.3 Q-表的迁移

上面用的Q表不是一个空白的表格，而是由Source Task下训练出来的Q表迁移过来进行的初始化。

Target Task和Source Task相差的只有时间参数和尺度参数

时间参数对应的是时钟变量，尺度参数对应的

在2个任务的输入、状态和时钟之间能够能够建立双射函数，自动机的结构不变

首先已知初始状态和接收状态的映射，逆推这个函数

---

5 实验

5.1 Case 1

9x9 走格子 存在motion uncertainty

每次初始状态随机选择

1. 前10000次训练收集数据，带标签+1/-1

2. 推理公式

3. 原任务上训练

4. 迁移Q表

5. 目标任务上训练

对比：

1. $\tau$-state Q-learning：收敛最慢 奖励低

2. 不考虑信息增益 收敛稍快奖励略低

3. 考虑信息增益 收敛略慢奖励高

4. 考虑信息增益 transfer learning 收敛快奖励高

5.2 实验2

• 目标任务与原任务环境大小不一样

• transfer的作用更小 - 红蓝差异不大

---

6 讨论

limitation：

由样本推理来的公式可能不完整

future work:

• 对于复杂任务，可以将总任务分解为更简单的子任务，或者将inference和learning交替迭代形成闭环

• 探索其他的强化学习算法