题目描述：

import sympy
from gmpy2 import gcd, invert
from random import randint
from Crypto.Util.number import getPrime, isPrime, getRandomNBitInteger, bytes_to_long, long_to_bytes
import base64

from zlib import *
flag = b"MRCTF{XXXX}"
base = 65537

def gen_prime(N):
    A = 0
    while 1:
        A = getPrime(N)
        if A % 8 == 5:
            break
    return A

def gen_p():
    p = getPrime(1024)
    q = getPrime(1024)
    assert (p < q)
    n = p * q
    print("P_n = ", n)
    F_n = (p - 1) * (q - 1)
    print("P_F_n = ", F_n)
    factor2 = 2021 * p + 2020 * q
    if factor2 < 0:
        factor2 = (-1) * factor2
    return sympy.nextprime(factor2)


def gen_q():
    p = getPrime(1024)
    q = getPrime(1024)
    assert (p < q)
    n = p * q
    print("Q_n = ", n)
    e = getRandomNBitInteger(53)
    F_n = (p - 1) * (q - 1)
    while gcd(e, F_n) != 1:
        e = getRandomNBitInteger(53)
    d = invert(e, F_n)
    print("Q_E_D = ", e * d)
    factor2 = 2021 * p - 2020 * q
    if factor2 < 0:
        factor2 = (-1) * factor2
    return sympy.nextprime(factor2)


if __name__ == "__main__":
    _E = base
    _P = gen_p()
    _Q = gen_q()
    assert (gcd(_E, (_P - 1) * (_Q - 1)) == 1)
    _M = bytes_to_long(flag)
    _C = pow(_M, _E, _P * _Q)
    print("Ciphertext = ", _C)
'''
P_n =  14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024336556028267742021320891681762543660468484018686865891073110757394154024833552558863671537491089957038648328973790692356014778420333896705595252711514117478072828880198506187667924020260600124717243067420876363980538994101929437978668709128652587073901337310278665778299513763593234951137512120572797739181693
P_F_n =  14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024099427363967321110127562039879018616082926935567951378185280882426903064598376668106616694623540074057210432790309571018778281723710994930151635857933293394780142192586806292968028305922173313521186946635709194350912242693822450297748434301924950358561859804256788098033426537956252964976682327991427626735740
Q_n =  20714298338160449749545360743688018842877274054540852096459485283936802341271363766157976112525034004319938054034934880860956966585051684483662535780621673316774842614701726445870630109196016676725183412879870463432277629916669130494040403733295593655306104176367902352484367520262917943100467697540593925707162162616635533550262718808746254599456286578409187895171015796991910123804529825519519278388910483133813330902530160448972926096083990208243274548561238253002789474920730760001104048093295680593033327818821255300893423412192265814418546134015557579236219461780344469127987669565138930308525189944897421753947
Q_E_D =  100772079222298134586116156850742817855408127716962891929259868746672572602333918958075582671752493618259518286336122772703330183037221105058298653490794337885098499073583821832532798309513538383175233429533467348390389323225198805294950484802068148590902907221150968539067980432831310376368202773212266320112670699737501054831646286585142281419237572222713975646843555024731855688573834108711874406149540078253774349708158063055754932812675786123700768288048445326199880983717504538825498103789304873682191053050366806825802602658674268440844577955499368404019114913934477160428428662847012289516655310680119638600315228284298935201
Ciphertext =  40855937355228438525361161524441274634175356845950884889338630813182607485910094677909779126550263304194796000904384775495000943424070396334435810126536165332565417336797036611773382728344687175253081047586602838685027428292621557914514629024324794275772522013126464926990620140406412999485728750385876868115091735425577555027394033416643032644774339644654011686716639760512353355719065795222201167219831780961308225780478482467294410828543488412258764446494815238766185728454416691898859462532083437213793104823759147317613637881419787581920745151430394526712790608442960106537539121880514269830696341737507717448946962021
'''

题目分析：

（先告知：此题有简便方法，即 直接将 P_n 和 Q_n 进行分解，得到两组 p,q（即用线上网站将n 分解得到p,q）将p,q带入生成factor2的代码中，即可得到 P,Q，之后就是常规的rsa解密了。以下是更详细深入的解析）

• 这题与 buu [GWCTF 2019]BabyRSA 1 比较像，分四个模块，第一个模块告诉我们生成素数的方法（对后面的分析没什么实质性关系）
• 第二个模块即生成 P 的过程（gen_p）:

告诉了我们 n = p * q , phi = (p-1) * (q-1) = p * q - (p+q) + 1 = n - (p+q) + 1
==>n = p * q , phi = n - (p+q) + 1
==>p + q = n - phi + 1
==>(p - q)^2 = (p+q)^2 - 4 * n
==>p - q = [(p-q)^2] ^0.5
==>p = [(p + q) + (p - q)] // 2
==>q = (p + q) - p

• 由上过程便可得出p,q,从而求出factor2,注意 p<q,若求出来的不符合则调换下位置
• 求P代码：

def get_p(n,phi):
    p_q = n - phi + 1 # p_q = p + q
    p_q_2 = p_q**2 - 4*n # p_q_2 = (p - q)^2
    p_q_1 = gmpy2.iroot(p_q_2,2)[0] # p_q_1 = p - q
    p = (p_q + p_q_1) // 2
    q = p_q - p
    if q < p:
        q,p = p,q
    factor2 = 2021 * p + 2020 * q
    if factor2 < 0:
        factor2 = (-1) * factor2
    P = sympy.nextprime(factor2)
    return P
P = get_p(P_n,P_F_n)

• 第三个模块即生成 Q 的过程（gen_q）,和上面生成 P 的过程很像，

不过此时已知的是 n = p * q , e * d = 1 mod phi
==>e * d - 1 = k * phi = k * (p - 1) * (q-1)
==>(e * d - 1) // p * q < (e * d - 1) // [p * q - (p + q) + 1] = k

• 求 Q 代码如下：

def get_q(n,phi):
    p_q = n - phi + 1 # p_q = p + q
    p_q_2 = p_q ** 2 - 4 * n # p_q_2 = (p - q)^2
    p_q_1 = gmpy2.iroot(p_q_2, 2)[0] # p_q_1 = p - q
    p = (p_q + p_q_1) // 2
    q = p_q - p
    if q < p:
        q, p = p, q
    factor2 = 2021 * p - 2020 * q
    if factor2 < 0:
        factor2 = (-1) * factor2
    Q = sympy.nextprime(factor2)
    return Q
k = ((Q_E_D-1)//Q_n)+1
phi = (Q_E_D - 1)//k
Q = get_q(Q_n,phi)

• 第四个模块则是告诉我们关于rsa的基础运算过程，想必这个大家都清楚，也不过多赘述了
• 以下是完整代码：

import gmpy2
from Crypto.Util.number import *
import sympy

def get_p(n,phi):
    p_q = n - phi + 1
    p_q_2 = p_q**2 - 4*n
    p_q_1 = gmpy2.iroot(p_q_2,2)[0]
    p = (p_q + p_q_1) // 2
    q = p_q - p
    if q < p:
        q,p = p,q
    factor2 = 2021 * p + 2020 * q
    if factor2 < 0:
        factor2 = (-1) * factor2
    P = sympy.nextprime(factor2)
    return P

def get_q(n,phi):
    p_q = n - phi + 1
    p_q_2 = p_q ** 2 - 4 * n
    p_q_1 = gmpy2.iroot(p_q_2, 2)[0]
    p = (p_q + p_q_1) // 2
    q = p_q - p
    if q < p:
        q, p = p, q
    factor2 = 2021 * p - 2020 * q
    if factor2 < 0:
        factor2 = (-1) * factor2
    Q = sympy.nextprime(factor2)
    return Q

base = 65537
P_n =  14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024336556028267742021320891681762543660468484018686865891073110757394154024833552558863671537491089957038648328973790692356014778420333896705595252711514117478072828880198506187667924020260600124717243067420876363980538994101929437978668709128652587073901337310278665778299513763593234951137512120572797739181693
P_F_n =  14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024099427363967321110127562039879018616082926935567951378185280882426903064598376668106616694623540074057210432790309571018778281723710994930151635857933293394780142192586806292968028305922173313521186946635709194350912242693822450297748434301924950358561859804256788098033426537956252964976682327991427626735740
Q_n =  20714298338160449749545360743688018842877274054540852096459485283936802341271363766157976112525034004319938054034934880860956966585051684483662535780621673316774842614701726445870630109196016676725183412879870463432277629916669130494040403733295593655306104176367902352484367520262917943100467697540593925707162162616635533550262718808746254599456286578409187895171015796991910123804529825519519278388910483133813330902530160448972926096083990208243274548561238253002789474920730760001104048093295680593033327818821255300893423412192265814418546134015557579236219461780344469127987669565138930308525189944897421753947
Q_E_D =  100772079222298134586116156850742817855408127716962891929259868746672572602333918958075582671752493618259518286336122772703330183037221105058298653490794337885098499073583821832532798309513538383175233429533467348390389323225198805294950484802068148590902907221150968539067980432831310376368202773212266320112670699737501054831646286585142281419237572222713975646843555024731855688573834108711874406149540078253774349708158063055754932812675786123700768288048445326199880983717504538825498103789304873682191053050366806825802602658674268440844577955499368404019114913934477160428428662847012289516655310680119638600315228284298935201
Ciphertext =  40855937355228438525361161524441274634175356845950884889338630813182607485910094677909779126550263304194796000904384775495000943424070396334435810126536165332565417336797036611773382728344687175253081047586602838685027428292621557914514629024324794275772522013126464926990620140406412999485728750385876868115091735425577555027394033416643032644774339644654011686716639760512353355719065795222201167219831780961308225780478482467294410828543488412258764446494815238766185728454416691898859462532083437213793104823759147317613637881419787581920745151430394526712790608442960106537539121880514269830696341737507717448946962021

p = get_p(P_n,P_F_n)
k = ((Q_E_D-1)//Q_n)+1
phi = (Q_E_D - 1)//k
q = get_q(Q_n,phi)
d = gmpy2.invert(base,(p-1)*(q-1))
m = pow(Ciphertext,d,p*q)
print(long_to_bytes(m))

• 最后flag{Ju3t_@_31mp13_que3t10n}

收获与体会：

• 总之通过这题对rsa又有了更深的理解，对某些的模块的运用也更加熟练
• 看大佬的wp,原来 k 还能这么求，真的想不到
• k的详细解析：

这里是引不等式两边的分母一个pq，一个pq-(p+q)+1相差并不大，并且还是整除，所以估计(ed-1)//pq和(ed-1)//(pq-(p+q)+1)差值不到1用

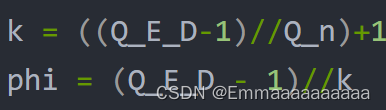
然后这里两次整除后，后面小数部分应该都省略掉了