先看题:

首先来看一下题目的要求:利用给定的边来构造一个有向无环图。
那么什么是有向无环图呢?我们来搜索一番:"所谓有向无环图其实就是:有方向的边;这些边在一个图中不会构成一个闭合的环路。"然后我们又发现:拓扑排序是对DAG的顶点进行排序,使得对每一条有向边(u, v),均有u(在排序记录中)比v先出现。亦可理解为对某点v而言,只有当v的所有源点均出现了,v才能出现。
也就是说,对样例中的图进行拓扑排序的判断,如果发现这个图能根据给出的有向边进行拓扑排序,说明这个图是有向无环图,否则就肯定不是有向无环图(有环存在)。
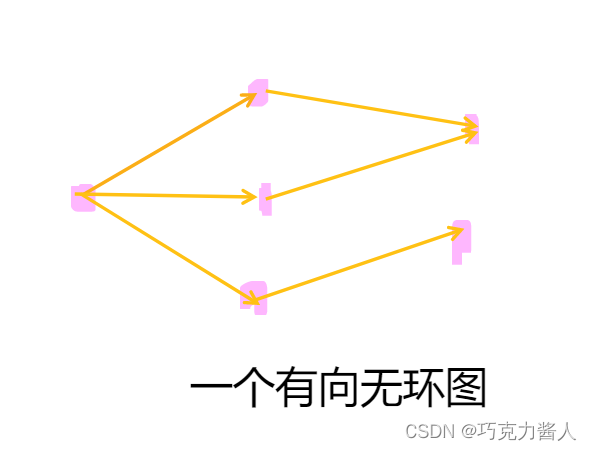
如果只考虑有向边,发现这个图就不能拓扑排序了,那么我们直接输出NO。为什么呢?因为现有的有向边中都存在环,那么无论对无向边进行如何的处理,都不会把这个环消掉,所以这个图仍然是一个有环的图。
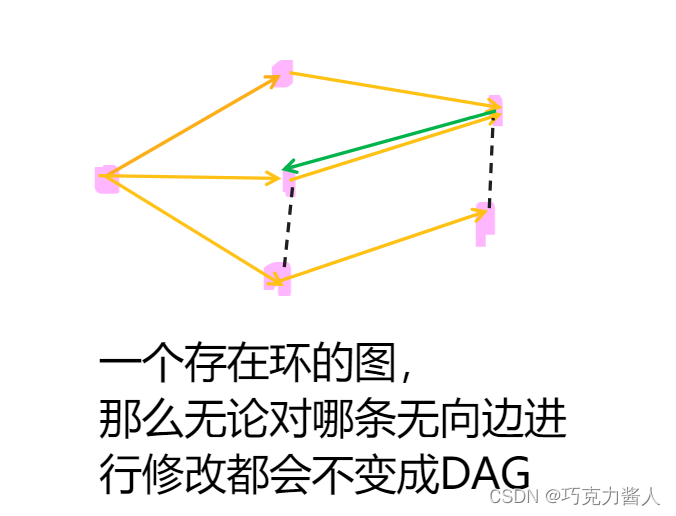
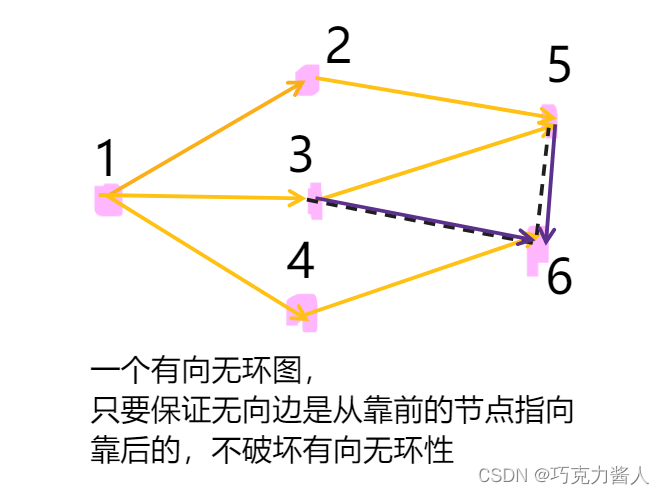
但是如果当前的有向边构造了一个DAG,那么在剩余的无向边的基础上我们能够保证一定构造出一个DAG吗?答案是可以的。因为在有向边的基础上,我们已经构造出了一个DAG,也就是说知道了这个DAG的拓扑排序方式,那么自然知道了每个节点在拓扑排序中的先后位置。只要保证对每条有向边,都可以从拓扑排序中靠前的节点指向靠后的节点,那么就一定能保证不产生环,构造得到一个DAG。
好了,思路理清了,我们开始写代码吧。
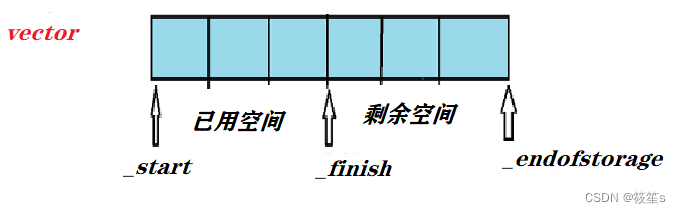
之前写拓扑排序都是用vector写,这次看了y总的代码,直接用数组写的,我就照搬了。然后把代码中可能看不明白的解释一下。
首先,对于图的数据结构,我们使用了邻接表的结构,原来一般采用邻接矩阵,邻接矩阵虽然比较简单,但是空间复杂度比较高。
邻接表是一个存储了所有图中节点的数组,然后数组中的每个元素对应和当前节点相邻的节点组成的。
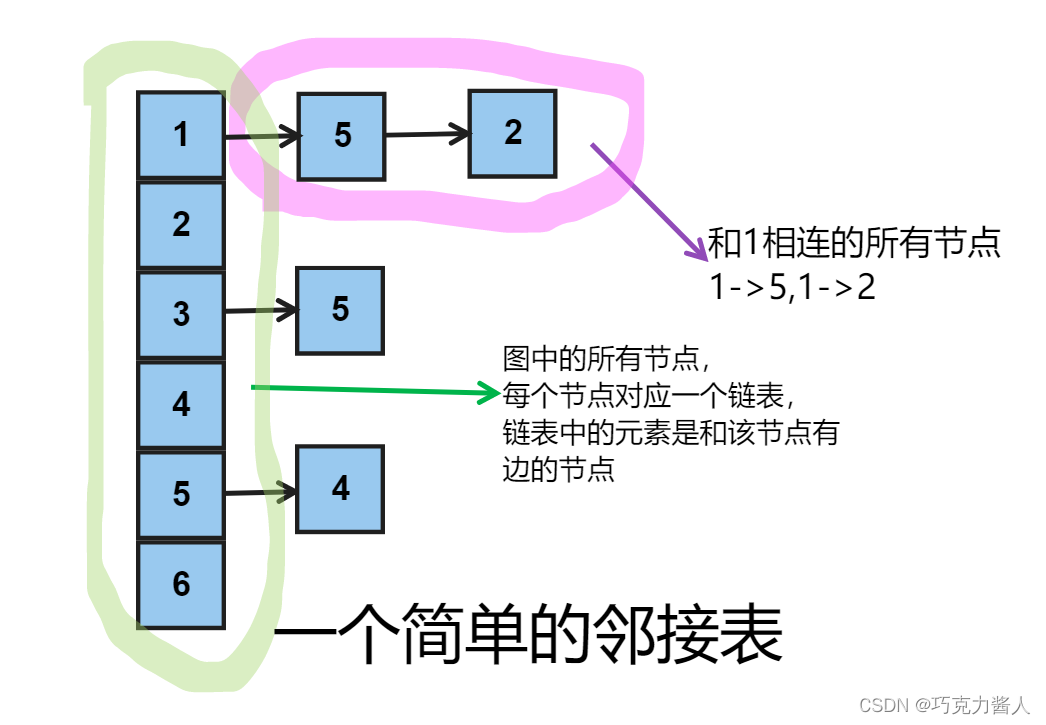
我们用h[i]表示第i个节点在邻接表中对应的头节点,e[i]代表的是第i条边对应的被指向的节点(比如:第三条边是a->b,那么e[3] = b.)ne[i]代表的是当前节点的下一个节点,相当于链表中next指针指向的节点,idx是每条边的索引(虽然这么说,但是反映到邻接表中就是每个节点的索引)。
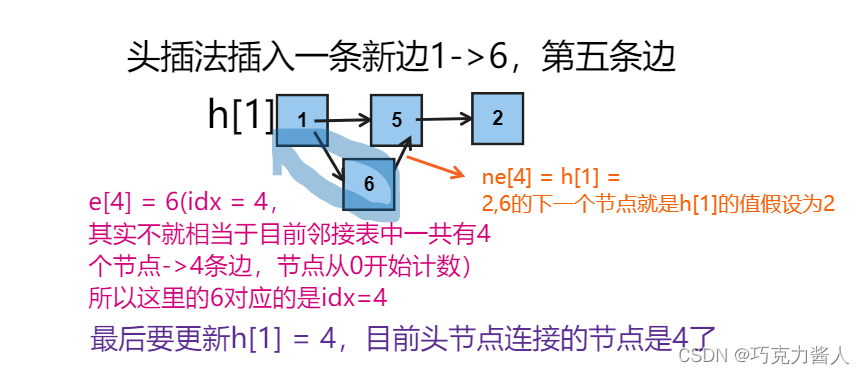
这样好像明白点了。
拓扑排序用的数组模拟队列,但是还比较简单,就画个草图,不详细写了。
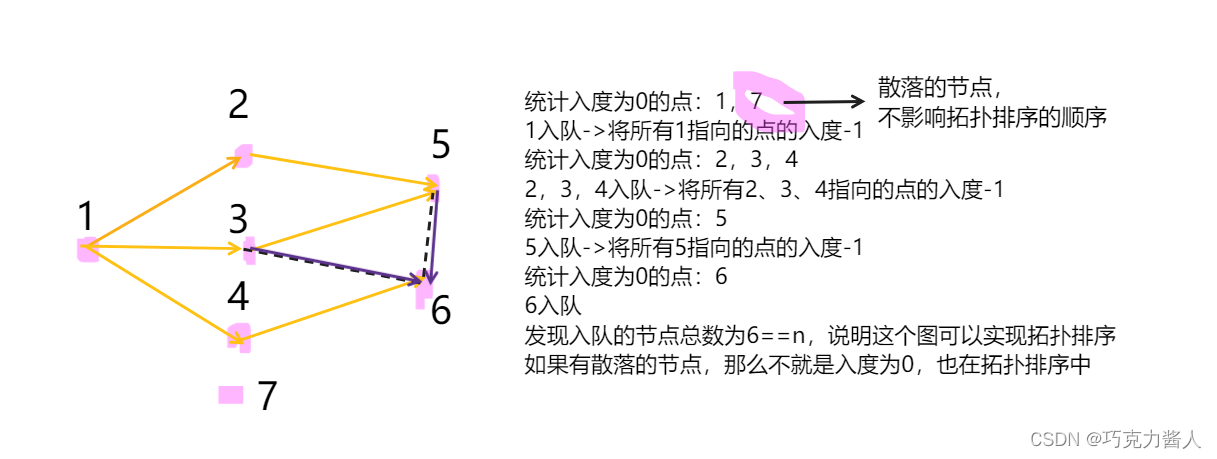
然后记得用pos记录拓扑排序中每个节点的顺序,在为无向边添加方向的时候,从靠前的节点指向靠后的节点。
代码如下:
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<set>
//#define ll long long
const int N = 200010, M = 200010;
int n, m, k;
//h是邻接表的表头,e是存储每条边对应的节点,ne是当前节点的下一个节点,idx是节点的索引
int h[N], e[M], ne[M], idx;
int d[N];
struct Edge{
int a, b;
}edges[M]; //存储每条边
int q[N], pos[N]; //进行拓扑排序的队列,以及每个点在排序中的位置
void add(int a, int b){ //插入一条从a->b的有向边
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
bool topsort(){
int hh = 0;
int tt = -1;
for(int i = 1; i <= n; i++){
if(!d[i]){
q[++tt] = i;
pos[i] = tt;
}
}
while(hh <= tt){ //遍历队列,hh是队头,tt是队尾
int t = q[hh++];
for(int i = h[t]; i != -1; i = ne[i]){
int j = e[i]; //其实就是相当于查找这条边指向的节点
if(--d[j] == 0){
q[++tt] = j;
pos[j] = tt;
}
}
}
return tt == n - 1; //tt是从-1开始的
}
int main(){
int t;
scanf("%d", &t);
while(t--){
scanf("%d%d", &n, &m);
idx = 0;
memset(d, 0, (n + 1) * 4); //int四个字节,如果用sizeof容易超时
memset(h, -1, (n + 1) * 4);
for(int i = 0; i < m; i++){
int t, x, y;
scanf("%d%d%d", &t, &x, &y);
if(t) {
add(x, y);
++d[y];
}
edges[i] = {x, y}; //先把无向边存上
}
if(!topsort()) puts("NO");
else{
puts("YES");
for(int i = 0; i < m; i++){
int a = edges[i].a;
int b = edges[i].b;
if(pos[a] < pos[b]) printf("%d %d\n", a, b); //从靠前的点指向靠后的点
else printf("%d %d\n", b, a);
}
}
}
return 0;
}
ok,就这么多,着急给我妈打电话去了。
借鉴的题解(其实是代码来源):
AcWing 3696. 构造有向无环图【DAG + 拓扑排序】 - AcWing
AcWing 3696. 构造有向无环图(AcWing杯 - 周赛) - AcWing
https://www.cnblogs.com/en-heng/p/5085690.html