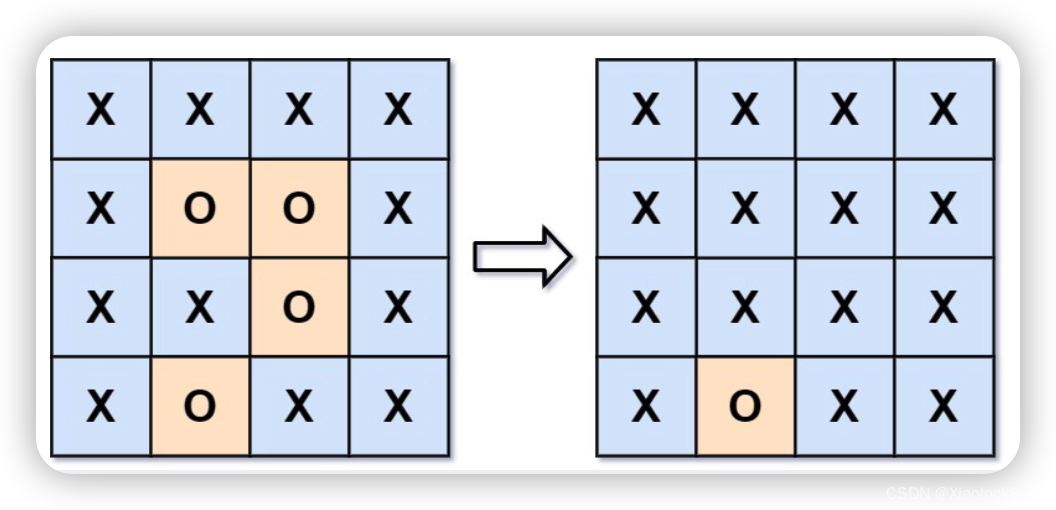
BELS: A BROAD ENSEMBLE LEARNING SYSTEM FOR DATA STREAM CLASSIFICATION
摘要:这篇文章主要是将BLS推广到适用于在线学习的邻域,提出了其如何进行适合在线学习的增量更新,以及面对概念漂移的适应
所提出的算法BELS
稀疏特征映射的更新
在BLS原论文也提到了如何更好的提取特征,然后文中介绍了利用稀疏自编码器的方式并利用ADMM求解权重的过程。那么为了让这个过程能够适用于在线学习中数据以块形式到达的特征,本文提出了这些修改。本来这个特征节点权重的更新是:

其中 z z z代表映射后的特点,而 w w w就是不停迭代更新的权重,即 X W = Z XW=Z XW=Z。 ρ \rho ρ是大于0的常数。S函数是:

原文中是希望利用数据然后不断地更新这个权重,达到更好的提出特征效果。
那么如果将其应用到以块到达的数据,需要先知道一个理论(原文中有证明过程),即假设有两个矩阵A和B,具有不同的行数但具有相同的列数,那么如果将这两个矩阵在行方向进行拼接为C,那么有:
C
T
C
=
A
T
A
+
B
T
B
C^TC=A^TA+B^TB
CTC=ATA+BTB
那么假设
T
1
=
z
T
X
,
T
2
=
z
T
z
T_1=z^TX,T_2=z^Tz
T1=zTX,T2=zTz,则到达新的数据块加入相当于z和X都增加行数,也就是原来的z和X和新来的z和X组成了新的T,因此可以利用上述公式,即:
T
1
k
=
∑
i
=
1
k
T
1
i
T
2
k
=
∑
i
=
1
k
T
2
i
T_{1k}=\sum_{i=1}^kT_{1i}\\T_{2k}=\sum_{i=1}^kT_{2i}
T1k=i=1∑kT1iT2k=i=1∑kT2i
因此特征映射权重新的更新公式为:

完成了特征节点的生成后,增强节点就暗战原始BLS的方法执行。因此特征节点和增强节点的生成过程如下所示:

伪逆的更新
由于原始BLS是一次性按照所有输入数据来计算伪逆,因此需要对伪逆更改为适用于在线学习的增量求解形式。原始伪逆求解公式为:
W
=
(
λ
I
+
A
A
T
)
−
1
A
T
Y
W=(\lambda I+AA^T)^{-1}A^TY
W=(λI+AAT)−1ATY
当前时间步为k,令
A
t
=
A
k
T
A
k
,
D
t
=
A
k
T
Y
K
A_t=A^T_kA_k,D_t=A^T_kY_K
At=AkTAk,Dt=AkTYK,则继续由上述理论可知:
A
t
k
=
∑
i
=
1
k
A
t
i
D
t
k
=
∑
i
=
1
k
D
t
i
A_{tk}=\sum_{i=1}^kA_{ti}\\D_{tk}=\sum_{i=1}^kD_{ti}
Atk=i=1∑kAtiDtk=i=1∑kDti
因此伪逆的更新形式为:
W
=
(
λ
I
+
A
t
k
)
−
1
D
t
k
W = (\lambda I + A_{tk})^{-1}D_{tk}
W=(λI+Atk)−1Dtk
因此权重的求解伪代码为:

预测输出计算为:

应对概念漂移
其思路是共用特征节点和增强节点,然后将每一个输出层作为一个基分类器来做集成。