题目链接

leetcode——在线链接

题目描述

给你一个 m x n 的矩阵 board ，由若干字符 ‘X’ 和 ‘O’ ，找到所有被 ‘X’ 围绕的区域，并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。

题目示例

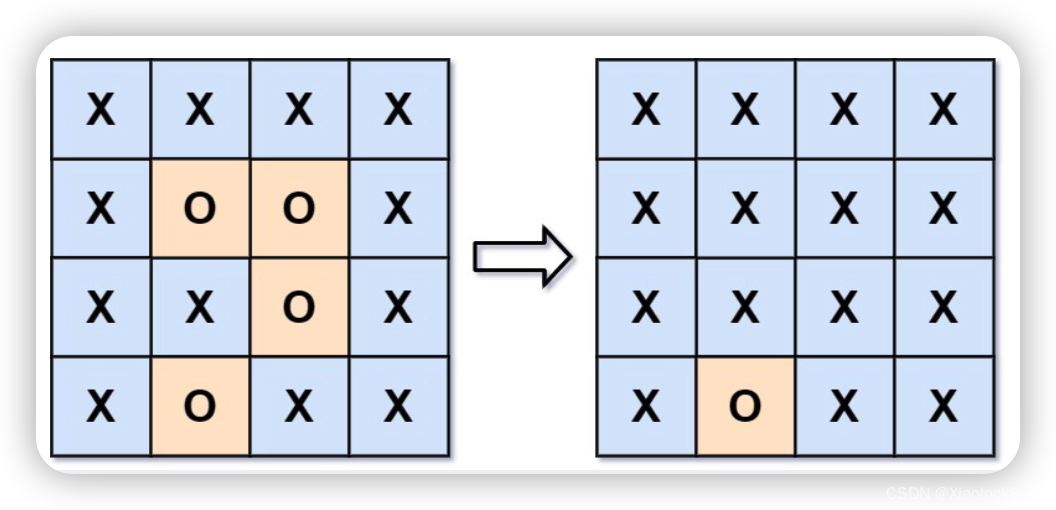
在这里插入图片描述
输入：board = [[“X”,“X”,“X”,“X”],[“X”,“O”,“O”,“X”],[“X”,“X”,“O”,“X”],[“X”,“O”,“X”,“X”]]
输出：[[“X”,“X”,“X”,“X”],[“X”,“X”,“X”,“X”],[“X”,“X”,“X”,“X”],[“X”,“O”,“X”,“X”]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 ‘O’ 都不会被填充为 ‘X’。任何不在边界上，或不与边界上的 ‘O’ 相连的 ‘O’ 最终都会被填充为 ‘X’。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

输入：board = [[“X”]]
输出：[[“X”]]

题目提示

m == board.length
n == board[i].length
1 <= m, n <= 200
board[i][j] 为 ‘X’ 或 ‘O’

解题思路

使用深度优先搜索

这道题就像围棋一样，如果四面八方都被X包围了，那么这些O就都要变成X，而只有通到外面的O才不会变成X

因此，我们只需要确定最外面一排的O的位置，并且将所有与之相连的O都标记出来，最后将所有未标记的O都变成X即可

定义一个isUsed数组，记录当前位置是否被遍历过
定义一个DFS方法，其参数分别为：board，行数，列数，当前所在行，当前所在列，isUsed数组

在DFS方法中，先将这个位置的O标记成A，然后分别遍历其上下左右四个位置，如果未越界并且是O，那么继续往下递归

最终，不能连接到外界的O还是O，将这些O变成X，而所有能够连接到外部的O刚刚被我们变成A，现在再遍历数组将这些A变回O即可

代码

public class Solution {
    int[][] nextPosition = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
    public void DFS(char[][] board, int row, int col, int curX, int curY, boolean[][] isUsed){
        //标记当前位置为联通的
        board[curX][curY] = 'A';
        isUsed[curX][curY] = true;

        //遍历下一个位置
        for (int i = 0; i < 4; i++) {
            int newX = curX + nextPosition[i][0];
            int newY = curY + nextPosition[i][1];
            //判断是否越界
            if(newX >= row || newX < 0 || newY >= col || newY < 0){
                continue;
            }
            if(board[newX][newY] == 'O'){
                DFS(board, row, col, newX, newY, isUsed);
            }
        }
    }
    public void solve(char[][] board) {
        if(board == null){
            return;
        }
        int row = board.length;
        int col = board[0].length;
        boolean[][] isUsed = new boolean[row][col];

        for (int i = 0; i < col; i++) {
            if(board[0][i] == 'O'){
                DFS(board, row, col, 0, i, isUsed);
            }
            if(board[row - 1][i] == 'O'){
                DFS(board, row, col, row - 1, i, isUsed);
            }
        }

        for (int i = 0; i < row; i++) {
            if(board[i][0] == 'O'){
                DFS(board, row, col, i, 0, isUsed);
            }
            if(board[i][col - 1] == 'O'){
                DFS(board, row, col, i, col - 1, isUsed);
            }
        }

        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                //被包围
                if(board[i][j] == 'O'){
                    board[i][j] = 'X';
                }
                //没被包围
                if(board[i][j] == 'A'){
                    board[i][j] = 'O';
                }
            }
        }
    }
}