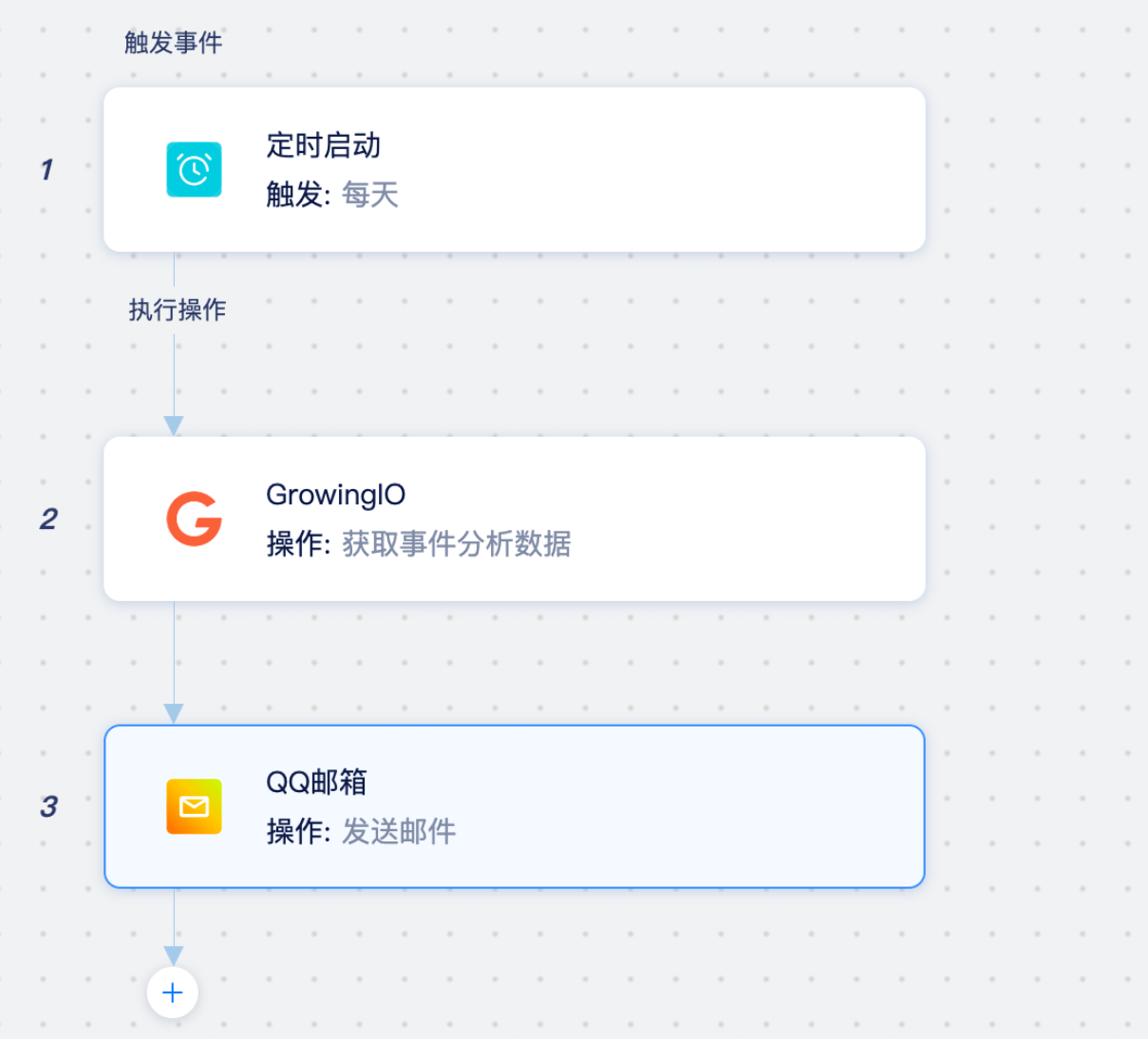
这篇文章使用了对比学习进行了聚类，一种端到端的离线聚类模型。

主要流程

Feature model

比较主流的句向量编码器SBERT。本文主要使用两个损失函数去微调SBERT的参数。使得SBERT的生成的特征表示具有以下两个特点：

• 簇间距离拉大（inter-cluster）
• 簇内距离缩小（intra-cluster）

对于数据 $x$， 编码：$e=\Phi (x)$

微调完成之后，将得到的 Feature Matrix ，使用K-means进行聚类。典型的离线聚类（outline-cluster）

cluster head

聚类头主要是用这篇paper的思想。

使用 SBERT 对数据进行编码得到 Feature Matrix，然后利用K-means算法进行聚类。得到K（数据集 簇类的数量）个聚类中心。并将他们设置成簇类头的初始参数。
每个前向传播会使用特征向量 $x$ 和聚类中心参数 $\mu$，结合t-student分布生成一个概率矩阵Q：
$$q_{i,k}=\frac{(1+||e_i-{\mu }_k|{|}_2^2/\alpha {)}^{-\frac{\alpha +1}{2}}}{{\sum }_{k^{\prime }=1}^K(1+||e_i-{\mu }_{k^{\prime }}|{|}_2^2/\alpha {)}^{-\frac{\alpha +1}{2}}}$$
其中，$\alpha$是超参数，$q_{i,k}$ 表示数据 $x_i$属于 簇$k$的概率。
然后再使用一个辅助函数，生成一个目标概率分布，这个函数的特点是将Q中每一行数值比较大的元素变得更大一点，相当于是将置信度比较高的数据着重学习一下。
辅助概率分布P:
$$p_{i,k}=\frac{q_{jk}^2/f_k}{{\sum }_{k^{\prime }}{q}_{jk}^2/f_{k^{\prime }}}$$
其中，$f_k={\sum }_{i=1}^M{q}_{ik}$, $M$ 是batch size 的大小。
最后使用KL散度损失函数，使Q的分布不断向P的分布靠近。

这种做法有三种好处：

• 提高聚类的纯度
• 注重使用置信度高的数据
• 归一化每个之心的损失贡献，防止大簇扭曲数据的特征分布空间。（对这一点我存在质疑，当面对长尾数据集的时候，归一化每个质心的损失贡献会不会起到反作用？）

Contrastive head

这一块的工作相对来说多一点，会涉及到数据增强。
一个数据$x_i$，经过两种数据增强得到 $x_i^a,x_i^b$，在经过编码得到 z i { a , b } = Φ ( x i { a , b } ) z_i^{\{a, b\}} = \Phi(x_i^{\{a, b\}}) zi{a,b}​=Φ(xi{a,b}​)。这篇论文采用了基于上下文的文本增强方式，并和反译法和增删词法做了比较。并说明对于自己的模型，基于上下文方式的文本增强效果更好。
聚类头的就够很简单：一个三层的非线性MLP。
具体的学习方式就是对比学习的基本范式:
$$\begin{gathered} {\hat{l}}_i^a=-\log \frac{\exp (s(z_i^a,z_i^b)/{\tau }_I)}{{\sum }_{j=1}^M[\exp (s(z_i^a,z_j^a)/{\tau }_I)+\exp (s(z_i^a,z_j^b)/{\tau }_I)]} \\ {\hat{l}}_i^b=-\log \frac{\exp (s(z_i^a,z_i^b)/{\tau }_I)}{{\sum }_{j=1}^M[\exp (s(z_i^b,z_j^a)/{\tau }_I)+\exp (s(z_i^b,z_j^b)/{\tau }_I]} \end{gathered}$$
总的损失函数：
$$L_{ins}=\frac{1}{2M}\sum _{i=1}^N({\hat{l}}_i^a+{\hat{l}}_i^b)$$
其中，${\tau }_I$ 是温度参数，$M$ 是batch size的大小，$s(\cdot )$ 是相似性度量，具体表达为：$s(z_i,z_j)=z_i^T{z}_j/||z_i|{|}_2\cdot ||z_j|{|}_2$。

结果展示

效果显而易见。