堆的概念结构及实现

news2024/11/15 17:24:11

文章目录

  • 1.堆的概念及结构
  • 2.堆的实现
    • 2.1父子节点之间的关系
    • 2.2堆的向上排序算法
    • 2.3 堆的删除
    • 2.4堆的向下排序算法
    • 2.5入堆
    • 2.6堆的创建
      • 2.6.1通过入堆实现（通过向上堆排序）
      • 2.6.2通过向下排序实现
      • 2.6.3两种方法比较
    • 2.7代码实现
      • 2.7.1函数声明
      • 2.7.2函数实现
      • 2.7.3代码测试

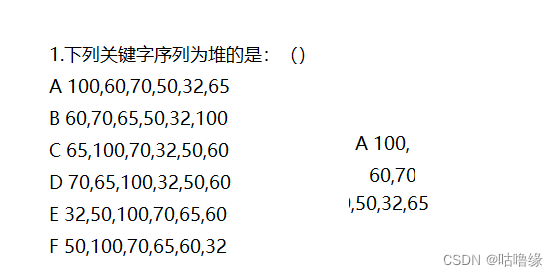
1.堆的概念及结构

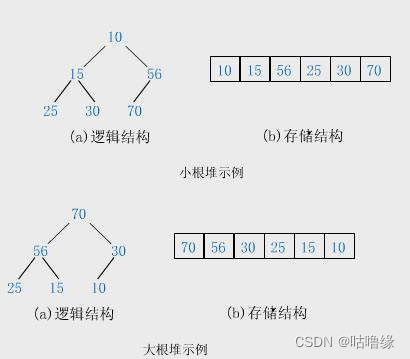
如果有一个关键码的集合K = { ， ， ，…， }，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足： <= 且 <= ( >= 且 >= ) i = 0，1，2…，则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

堆的性质：
堆中某个节点的值总是不大于或不小于其父节点的值；
堆总是一棵完全二叉树。

在这里插入图片描述

在这里插入图片描述

2.堆的实现

2.1父子节点之间的关系

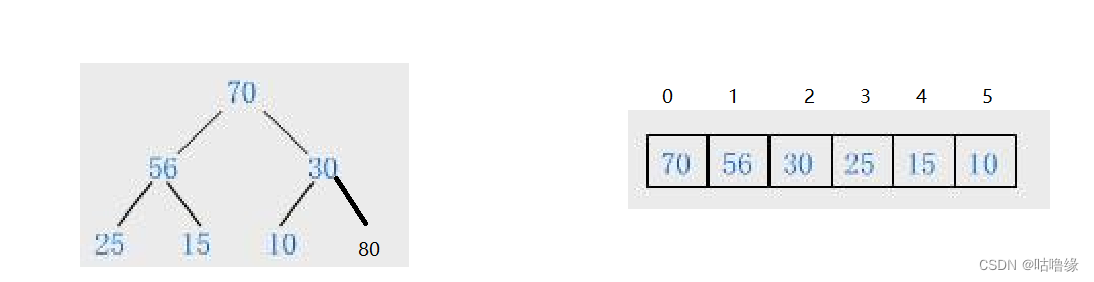
在这里插入图片描述
在此之前，我们先了解一下父子节点之间的关系
leftchild=parent2+1
rightchild=parent2+2
parent=(chile-1)/2

2.2堆的向上排序算法

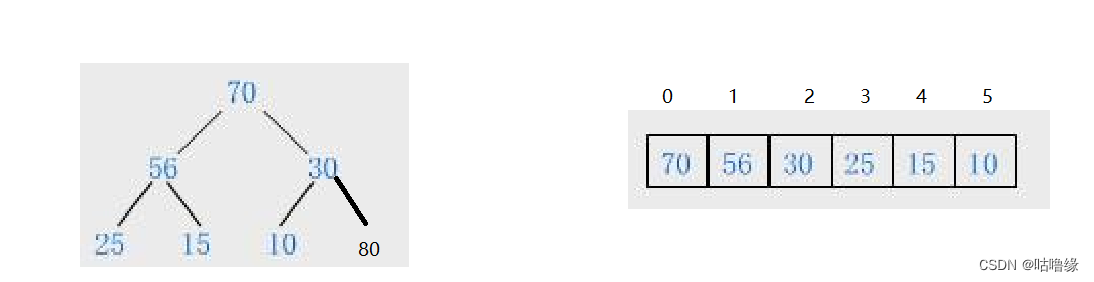
在这里插入图片描述
正如图上所示，我们插入一个80节点，显然它比它的祖先都要大，所以我们要调整堆这就用到了向上调整法
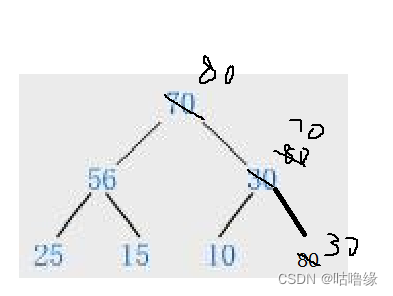
在这里插入图片描述
思路就是这样 代码如下：

void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;//定义父节点
	while (child > 0)//这里的判定条件可以有另外一种为parent>=0,
	虽然也可以实现函数但是当child=0时，parent=（0-1）/2=0，
	if语句不成立才break的，是非正常结束，所以不推荐
	{
		if (a[parent] < a[child])
		{
			Swap(&a[parent], &a[child]);//交换位置
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
	}

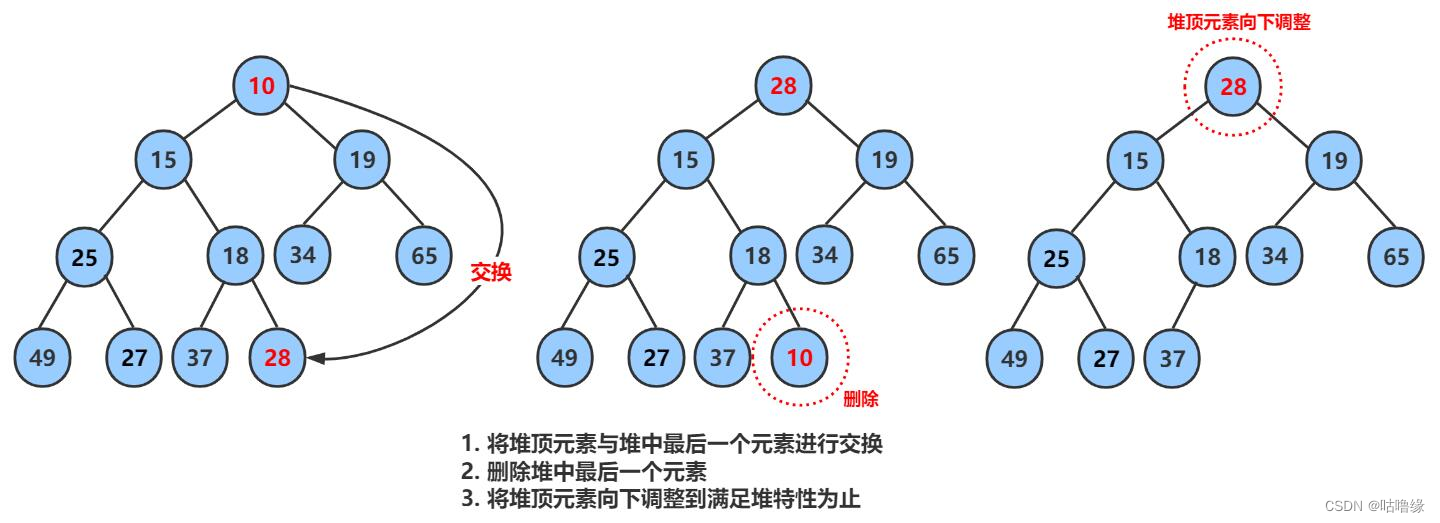
2.3 堆的删除

删除堆是删除堆顶的数据，将堆顶的数据根最后一个数据一换，然后删除数组最后一个数据，再进行向下调整算法。
在这里插入图片描述

void HeapPop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	Swap(&php->a[php->size - 1], &php->a[0]);
	php->size--;
	AdjustDown(php->a, php->size, 0);
}

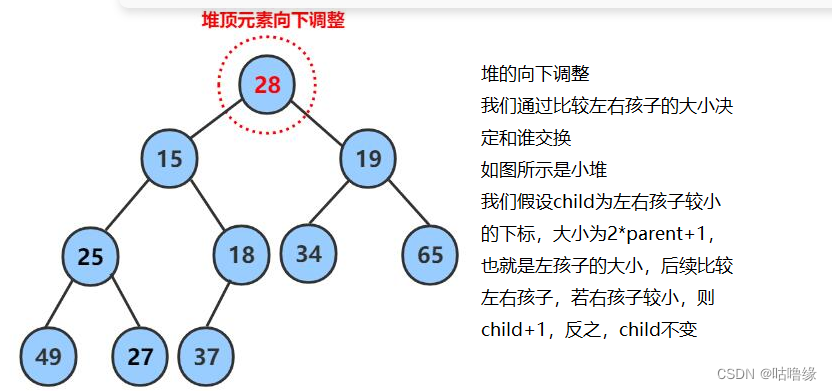
2.4堆的向下排序算法

在这里插入图片描述

void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = 2 * parent + 1;
	while (child < n)
	{
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = 2 * parent + 1;
		}
		else
			break;
	}
}

2.5入堆

void Heappush(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{
		int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}

	php->a[php->size] = x;
	php->size++;
	AdjustUp(php->a, php->size - 1);
}

2.6堆的创建

2.6.1通过入堆实现（通过向上堆排序）

这种方法也是比较投机取巧的方法了

// 堆的构建
void HeapCreate(HP* php, HPDataType* a, int n)
{
	assert(php);
	HeapInit(php);
	for (int i = 0; i < n; ++i)
	{
		HeapPush(php, a[i]);
    }
}

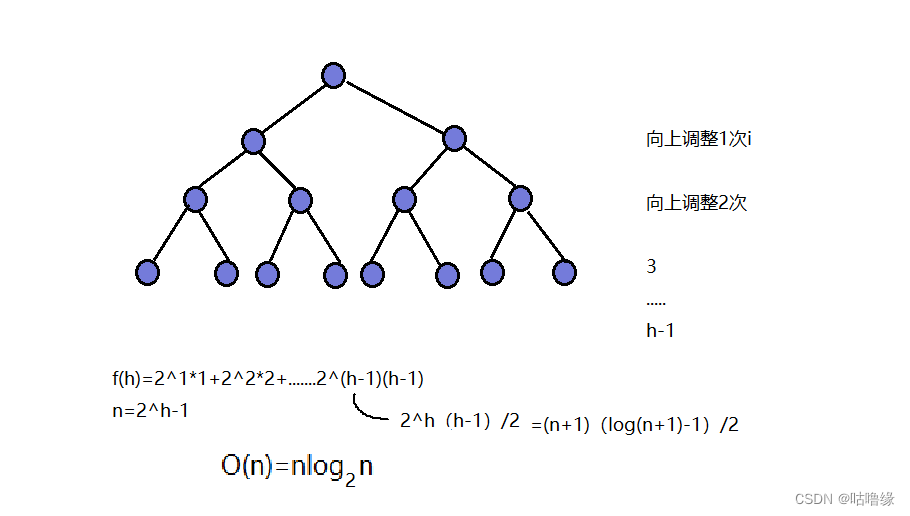
这种方法的时间复杂度
在这里插入图片描述

2.6.2通过向下排序实现

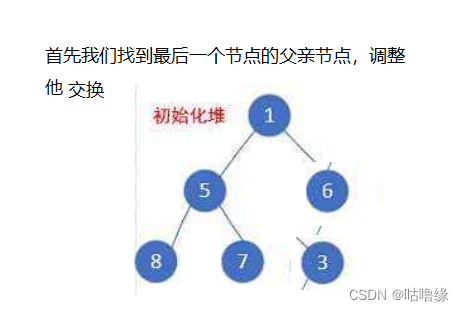
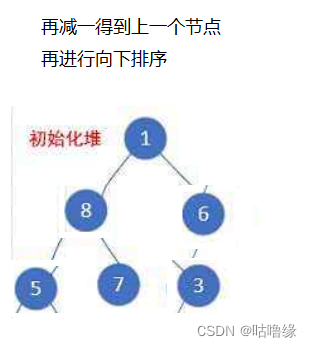
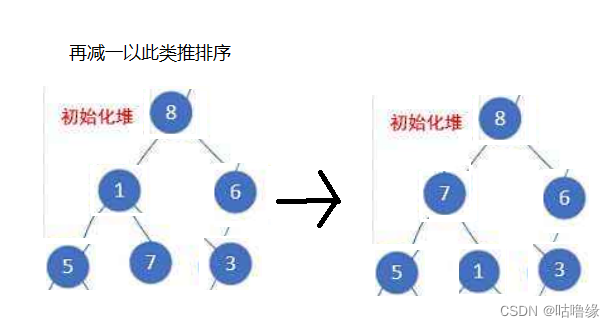
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

void HeapCreate(HP* php, HPDataType* a, int n)
{
	assert(php);
	php->a = (HPDataType*)malloc(php->a, sizeof(HPDataType)*n);
	if (php->a == NULL)
	{
		perror("realloc fail");
		exit(-1);
	}
	memcpy(php->a, a, sizeof(HPDataType)*n);
	php->size = php->capacity = n;

	// 建堆算法
	for (int i = (n-1-1)/2; i>=0; --i)
	{
		AdjustDown(a, n, i);
	}
}

这种方法时间复杂度
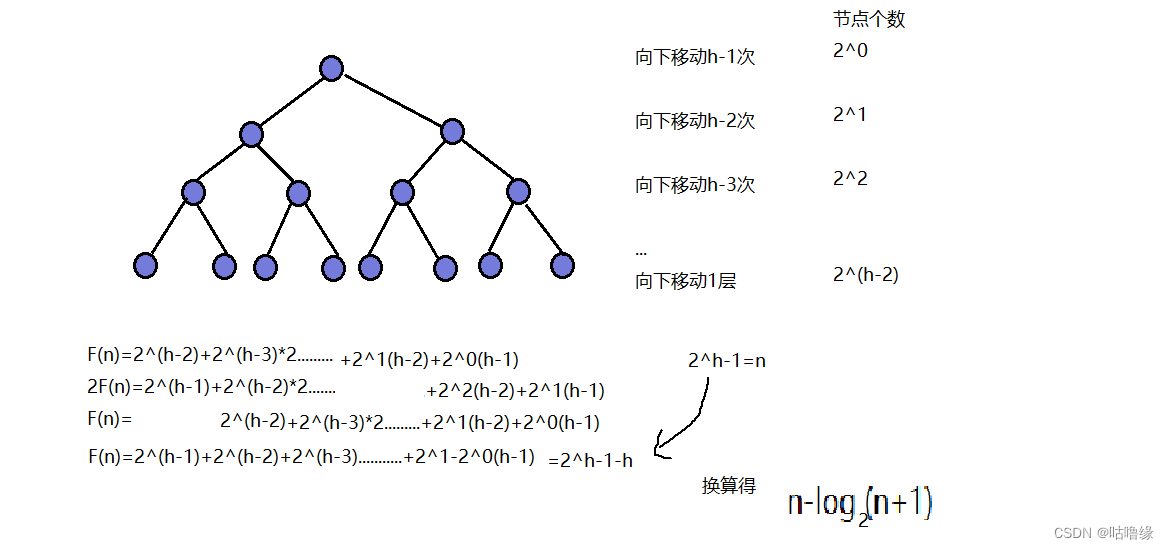
在这里插入图片描述

2.6.3两种方法比较

两种方法比较来说
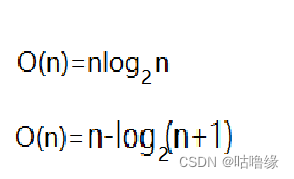
在这里插入图片描述
通过向下排序实现的创建堆方便太多了

2.7代码实现

2.7.1函数声明

#define _CRT_SECURE_NO_WARNINGS 1
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
#include<string.h>
typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;

}HP;
void HeapInit(HP* php);
void HeapDestory(HP* php);
void Heappush(HP* php, HPDataType x);
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
bool HeapEmpty(HP* php);
void HeapPrint(HP* php);
void HeapCreate(HP* php, HPDataType* a, int n);
void AdjustDown(HPDataType* a, int n, int parent);
void Swap(HPDataType* p1, HPDataType* p2);
void AdjustUp(HPDataType* a, int child);

2.7.2函数实现

#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"
void HeapCreate(HP* php, HPDataType* a, int n)
{
	assert(php);
	php->a = (HPDataType*)malloc( sizeof(HPDataType) * n);
	if (php->a == NULL)
	{
		perror("realloc fail");
		exit(-1);
	}
	memcpy(php->a, a, sizeof(HPDataType) * n);
	php->size = php->capacity = n;

	// 建堆算法
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDown(php->a, n, i);
	}
}
//void HeapCreate(HP* php, HPDataType* a, int n)
//{
//	assert(php);
//	HeapInit(php);
//	for (int i = 0; i < n; ++i)
//	{
//		Heappush(php, a[i]);
//	}
//}
void HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->size = php->capacity = 0;
}
void HeapDestory(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->capacity = php->size = 0;
}
void Swap(HPDataType* p1, HPDataType* p2)
{
	HPDataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[parent] < a[child])
		{
			Swap(&a[parent], &a[child]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}


}
void Heappush(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{
		int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}

	php->a[php->size] = x;
	php->size++;
	AdjustUp(php->a, php->size - 1);
}
void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = 2 * parent + 1;
	while (child < n)
	{
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = 2 * parent + 1;
		}
		else
			break;
	}
}
void HeapPop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	Swap(&php->a[php->size - 1], &php->a[0]);
	php->size--;
	AdjustDown(php->a, php->size, 0);
}
HPDataType HeapTop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	return php->a[0];
}
bool HeapEmpty(HP* php)
{
	assert(php);

	return php->size == 0;
}
void HeapPrint(HP* php)
{
	assert(php);
	for (int i = 0; i < php->size; ++i)
	{
		printf("%d ", php->a[i]);
	}
	printf("\n");
}

2.7.3代码测试

#define _CRT_SECURE_NO_WARNINGS 1

#include"Heap.h"
void test()
{
	int array[] = { 27, 15, 19, 18, 28, 34, 65, 49, 25, 37 };
	HP hp;
	HeapInit(&hp);
	HeapCreate(&hp, array, 10);
	HeapPrint(&hp);
}
int main()
{
	test();
}

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/382390.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

前端开发与vscode开发工具介绍

前端开发与vscode开发工具介绍

文章目录1、前端开发2、vscode安装和使用2.1、下载地址2.2、插件安装2.3、设置字体大小2.4、开启完整的Emmet语法支持2.5、创建项目2.6、保存工作区2.7、新建文件夹和网页1、前端开发 前端工程师“Front-End-Developer”源自于美国。大约从2005年开始正式的前端工程师角色被行…
阅读更多...
【Python入门第二十一天】Python 数组

【Python入门第二十一天】Python 数组

请注意&#xff0c;Python 没有内置对数组的支持&#xff0c;但可以使用 Python 列表代替。 数组 数组用于在单个变量中存储多个值&#xff1a; 实例 创建一个包含汽车品牌的数组&#xff1a; cars ["Porsche", "Volvo", "BMW"]运行实例 …
阅读更多...
【我的车载技术】 Android AutoMotive 之 init与zygote内核原理

【我的车载技术】 Android AutoMotive 之 init与zygote内核原理

init概述 init是一个进程&#xff0c;确切地说&#xff0c;它是Linux系统中用户空间的第一个进程。由于Android是基于Linux内核的&#xff0c;所以init也是Android系统中用户空间的第一个进程&#xff0c;它的进程号是1。作为天字第一号的进程&#xff0c;init被赋予了很多极其…
阅读更多...
FFmpeg最常用命令参数详解及应用实例

FFmpeg最常用命令参数详解及应用实例

FFMPEG堪称自由软件中最完备的一套多媒体支持库&#xff0c;它几乎实现了所有当下常见的数据封装格式、多媒体传输协议以及音视频编解码器&#xff0c;提供了录制、转换以及流化音视频的完整解决方案。 ffmpeg命令行参数解释 ffmpeg -i [输入文件名] [参数选项] -f [格式] [输出…
阅读更多...
lambada表达式

lambada表达式

负壹、 函数式编程 Java为什么要支持函数式编程&#xff1f; 代码简洁 函数式编程写出的代码简洁且意图明确&#xff0c;使用stream接口让你从此告别for循环。 多核友好 Java函数式编程使得编写并行程序从未如此简单&#xff0c;你需要的全部就是调用一下parallel()方法。 Jav…
阅读更多...
C++ -- STL简介、string的使用

C++ -- STL简介、string的使用

什么是STL STL(standard template libaray-标准模板库)&#xff1a;是C标准库的重要组成部分&#xff0c;不仅是一个可复用的组件库&#xff0c;而且是一个包罗数据结构与算法的软件框架。 STL的版本 原始版本&#xff1a;Alexander Stepanov、Meng Lee 在惠普实验室完成的原…
阅读更多...
Person p=new student()是什么意思

Person p=new student()是什么意思

记住&#xff1a;父类引用子类对象 Student t new Student(); 实例化一个Student的对象&#xff0c;这个不难理解。但当我这样定义时&#xff1a;Person p new Student(); 这代表什么意思呢&#xff1f; 很简单&#xff0c;它表示我定义了一个Person类型的引用&#xff0c;指…
阅读更多...
内大892复试真题16年

内大892复试真题16年

内大892复试真题16年 1. 输出三个数中较大数2. 求两个数最大公约数与最小公倍数3. 统计字符串中得字符个数4. 输出菱形5. 迭代法求平方根6. 处理字符串(逆序、进制转换)7. 寻找中位数8. 输入十进制输出n进制1. 输出三个数中较大数 问题 代码 #include <iostream>usin…
阅读更多...
如何保护页面端的企业邮箱

如何保护页面端的企业邮箱

作为日常工作交流中不可或缺的工具&#xff0c;电子邮件的安全性一直是备受关注的话题。页面是企业邮箱用户日常邮箱使用的重要接入终端&#xff0c;企业邮箱承载着企业的重要业务内容和关键数据。这个环节的安全问题会对企业产生深远的影响&#xff0c;信息安全建设的重要性不…
阅读更多...
CharGPT无法替代的职场发展底层逻辑

CharGPT无法替代的职场发展底层逻辑

​ 什么是职场发展的两大底层逻辑&#xff1f; 一为对事&#xff0c;一为对人&#xff0c;二者不可偏废&#xff0c;否则就会成为“职场上的瘸子”。 01 在刚开始工作的很长一段时间里&#xff0c;我遇到了同一个问题 - 虽然我对自己的工作认真负责&#xff0c;但职业发展却并…
阅读更多...
移动硬盘文件或目录损坏且无法读取？分享恢复数据的方法

移动硬盘文件或目录损坏且无法读取？分享恢复数据的方法

案例&#xff1a;移动硬盘提示无法访问&#xff0c;文件或目录损坏且无法读取&#xff1f; “这个移动硬盘两年没用了&#xff0c;今天拿出来找文件&#xff0c;插上电脑后移动硬盘打不开&#xff0c;提示无法访问&#xff0c;文件或目录损坏且无法读取。硬盘里有重要文件&…
阅读更多...
在字节跳动做了5年软件测试，12月无情被辞，想给划水的兄弟提个醒

在字节跳动做了5年软件测试，12月无情被辞，想给划水的兄弟提个醒

先简单交代一下背景吧&#xff0c;某不知名 985 的本硕&#xff0c;17 年毕业加入字节&#xff0c;以“人员优化”的名义无情被裁员&#xff0c;之后跳槽到了有赞&#xff0c;一直从事软件测试的工作。之前没有实习经历&#xff0c;算是5年的工作经验吧。 这5年之间完成了一次…
阅读更多...
SpringBoot异常处理

SpringBoot异常处理

目录 一、 错误处理 1. 默认规则 2. 定制错误处理逻辑 二、自定义异常处理 1. 实现 ErrorController 2. RestControllerAdvice/ControllerAdvice ExceptionHandler 实现自定义异常 3. 新建 UserController.class 测试 3 种不同异常的处理 4. 最终效果如下 补充 1. 参…
阅读更多...
【数据结构】八大经典排序总结

【数据结构】八大经典排序总结

文章目录一、排序的概念及其运用1.排序的概念2.常见排序的分类3.排序的运用二、常见排序算法的实现1.直接插入排序1.1排序思想1.2代码实现1.3复杂度及稳定性1.4特性总结2.希尔排序2.1排序思想2.3复杂度及稳定性2.4特性总结3.直接选择排序3.1排序思想3.2代码实现3.3复杂度及稳定…
阅读更多...
《数据治理行业实践白皮书》正式发布，开辟数据治理新范式（附下载）

《数据治理行业实践白皮书》正式发布，开辟数据治理新范式（附下载）

近日&#xff0c;作为首届未来数商大会协办单位之一&#xff0c;袋鼠云承办“首届未来数商大会——业数融合创新论坛”&#xff0c;与参会嘉宾共同探讨数据驱动企业业务增长提效的新思路。袋鼠云联合创始人、易知微CEO 宁海元发表主题演讲《数智视融合&#xff0c;构建数字产业…
阅读更多...
Docker安装Cassandra数据库，在SpringBoot中连接Cassandra

Docker安装Cassandra数据库，在SpringBoot中连接Cassandra

简介 Apache Cassandra是一个高度可扩展的高性能分布式数据库&#xff0c;旨在处理许多商用服务器上的大量数据&#xff0c;提供高可用性而没有单点故障。它是NoSQL数据库的一种。首先让我们了解一下NoSQL数据库的作用。 NoSQL 数据库 NoSQL数据库&#xff08;有时称为“Not …
阅读更多...
YOLO5-V7.0的python代码转成exe，方便离线部署

YOLO5-V7.0的python代码转成exe，方便离线部署

思路&#xff1a;用Pyinstaller打包&#xff0c;但有一些坑&#xff0c;踩完坑后成功运行&#xff0c;写个踩坑指南分享下。 前提&#xff1a;已经在conda 环境下安装完可以运行的yolo5代码&#xff0c;例如你的虚拟python环境叫yolo5&#xff0c;主代码是XXX.py&#xff08;这…
阅读更多...
数字IC手撕代码--低功耗设计 Clock Gating

数字IC手撕代码--低功耗设计 Clock Gating

背景介绍芯片功耗组成中&#xff0c;有高达 40%甚至更多是由时钟树消耗掉的。这个结果的原因也很直观&#xff0c;因 为这些时钟树在系统中具有最高的切换频率&#xff0c;而且有很多时钟 buffer&#xff0c;而且为了最小化时钟 延时&#xff0c;它们通常具有很高的驱动强度。 …
阅读更多...
《分布式技术原理与算法解析》学习笔记Day26

《分布式技术原理与算法解析》学习笔记Day26

流量控制 什么是流量控制&#xff1f; 网络传输中的流量控制就是让发送方发送数据的速度不要太快&#xff0c;这样可以让接收方来得及接收数据&#xff0c;通常使用滑动窗口的方式来实现。 滑动窗口是指在任意时刻&#xff0c;发送方都维持一个连续的允许发送的数据大小&…
阅读更多...
全国CSM敏捷教练认证将于2023年3月25-26开班，报名从速！

全国CSM敏捷教练认证将于2023年3月25-26开班，报名从速！

CSM&#xff0c;即Certified Scrum Master&#xff0c;是Scrum联盟发起的Scrum认证。 CSM可以帮助团队正确使用Scrum&#xff0c;从而提高项目整体成功的可能性。 CSM深刻理解Scrum的价值观、实践以及Scrum框架。 CSM是“服务型领导”&#xff0c;帮助Scrum团队一起紧密合作。 …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023